水下光场的角分布
当阳光进入水体时,它立即穿透表面,由于光子的散射,它的角度分布开始改变——变得更没有方向性,更分散。深度越大,至少被散射过一次的光子比例就越大。然而,产生的角度分布并不仅仅是散射的函数:光子的垂直运动越小,它穿过给定深度的路径长度就越大,它在该深度内被吸收的概率就越大。因此,越斜向运动的光子越强烈地被吸收所除去,这种效应阻止了一个完全各向同性场的建立。由此产生的角分布是由吸收和散射过程之间的相互作用决定的。最终,光强的角度分布呈现出一种固定的形式-称为渐近辐射分布-它是关于垂直轴对称的,其形状仅由吸收系数,散射系数和体积散射函数的值决定。338,636,1076,1092,1368美国的Whitney(1941)和爱尔兰的Poole(1945)根据独立的理论依据预测了这种平衡辐射分布将在极深处建立,Preisendorfer(1959)和Hojerslev和Zaneveld(1977)给出了它存在的数学证明。Jerlov和Liljequist(1938)在波罗的海进行的早期测量显示,随着深度的增加,辐射度分布向对称状态移动。Tyler(1960)在美国Pend Oreille湖精确到66米的测量表明,在这个近渐近深度,辐射度分布非常接近于预测的对称状态。
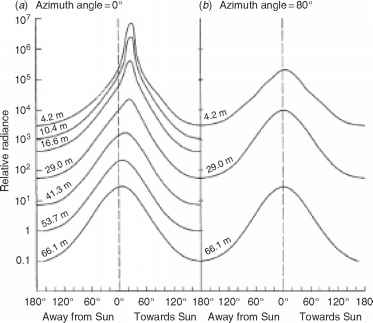
从辐射度分布随深度的变化可以看出,水下光场的角结构逐渐向渐近状态发展。如图6.11所示,这是基于Tyler(1960)在Pend Oreille湖的测量结果。图6.11a为太阳平面上不同垂直角度的辐亮度。在接近地表的地方,光场是高度定向的,大部分通量来自太阳的近似方向。随着深度的增加,辐射分布的峰值变得更宽,因为它的中心移向0 = 0°。最终的,渐近的,辐射分布将是对称的天顶。值得注意的是,在太阳平面上,即使在66米的高度,也还没有达到这种最终状态。图6.11b显示,在与太阳几乎成直角的平面上,即使在接近表面的地方,辐射度的分布也几乎是垂直对称的。在中间方位角上,存在介于图6.11a和图b之间的辐射度分布。
天顶角
图6.11不同深度水下光场辐射度分布。图为Tyler(1960)在美国Pend Oreille湖480 nm处的测量,太阳高度56.6°,散射系数0.285 m_1,吸收系数0.117m-1。(a)太阳平面内的辐射分布。(b)在与太阳平面几乎成直角的平面上的辐射分布。
天顶角
图6.11不同深度水下光场辐射度分布。图为Tyler(1960)在美国Pend Oreille湖480 nm处的测量,太阳高度56.6°,散射系数0.285 m_1,吸收系数0.117m-1。(a)太阳平面内的辐射分布。(b)在与太阳平面几乎成直角的平面上的辐射分布。
图6.12以极坐标图的形式展示了Pend Oreille湖的近渐近辐射度分布。如果在天然水中,散射与吸收的比率增加到较高的水平,那么这种渐近辐射分布的极坐标图的形状倾向于一个圆(即光场接近完全扩散状态)。然而,如果散射相对于吸收减少到一个较低的值,那么极坐标图就呈现出一个向下的窄铅笔的形式Aas和Hojerslev(1999)分析了水下角辐射分布的大型数据集,其中70个来自地中海西部,12个来自美国爱达荷州的Pend Oreille湖。他们能够找到两个简单的函数,它们之间可以用来描述角亮度分布。函数表示近似于方位角辐射分布的椭圆的偏心率。
-
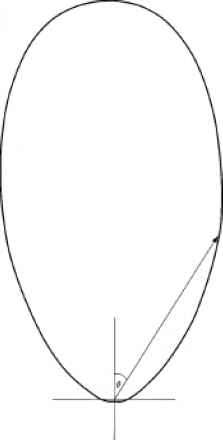
- 图6.12美国Pend Oreille湖的近渐近辐射度,绘制为极坐标图。数据与图6.11b中最低曲线的数据相同。
极坐标:它提供了在给定深度向下辐亮度的方位平均值,平均误差<7%,向上辐亮度的方位平均值,平均误差约1%。参数a对向上辐射度的方位平均值起着类似的作用。它描述了向上辐射度的方位平均值的天顶角依赖性,在清澈的海水中平均误差<7%,在浑浊的湖水中增加到<20%。确定e需要测量亮度的两个方位值:a可以通过测量L(180°)、Eu和E0u这两个量来获得。
在光合作用的背景下,亮度的意义是什么。分布与光强衰减的快速性有关

«f ítr ait ti&L acL \wr i4£r isi>- iao'
Zifnith anjii
图6.13浑浊湖中水下光场各方位角平均辐射度分布。在实测数据的基础上,采用Kirk (l98la, c)方法进行蒙特卡罗计算,得到了澳大利亚Burley Griffin湖的总PAR辐射亮度值吸收和散射特性(吸收光谱,图3.9b;散射系数15.0m-1;太阳高度32°)。
OZ&rn fl.60n,
«f ítr ait ti&L acL \wr i4£r isi>- iao'
Zifnith anjii
图6.13浑浊湖中水下光场各方位角平均辐射度分布。采用Kirk (l98la, c)方法,根据实测的吸收和散射特性(吸收光谱,图3.9b;散射系数15.0m-1;太阳高度32°)。
与深度。在每个垂直角上辐射度的方位分布与此无关。因此,为了简单起见,用每个垂直角度上所有方位角上的平均亮度来表示任意深度光场的角度分布是合理的。图6.13显示了通过蒙特卡罗方法计算的澳大利亚湖泊PAR在深度增加时的一系列亮度分布。在这种情况下,更快地达到最终对称分布的方法部分是对所有方位角进行平均的结果,部分是因为相对于彭德奥莱耶湖,这个湖的散射相对于吸收增加了。
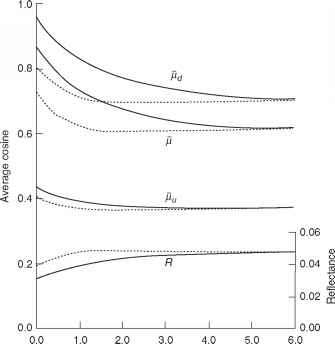
一种更简单的表达光场角度分布的方法是用三个平均余弦(见§1.3)和辐照度反射率表示。在图6.14中,通过蒙特卡罗计算得到的这些参数的值702,704与b/a = 5.0的水中光学深度(Z = Kdz)的比值。平均余弦和平均向下余弦最初都在值上急剧下降,但随着光的角度分布接近渐近辐射分布开始趋于平稳。在深度(zeu, Z = 4.6)以外的角度分布没有进一步的显著变化,在该深度,辐照度已降低到地下值的1%,实际上是大部分
光学深度,Z
图6.14 b/a = 5时,水中下沉(fid)、上涌(fiu)和总(fi)通量及辐照度反射率(R)的平均余弦值随光学深度(Z = Kdz)的变化通过蒙特卡罗计算得到的数据。702(垂直入射光_。45°入射光)
光学深度,Z
图6.14 b/a = 5时,水中下沉(fid)、上涌(fiu)和总(fi)通量及辐照度反射率(R)的平均余弦值随光学深度(Z = Kdz)的变化通过蒙特卡罗计算得到的数据。702(垂直入射光_。45°入射光)
变化发生在zm (Z = 2.3)到达之前。fi随深度向其渐近值的减小近似成指数值得注意的是,对于垂直入射的光,fid从略小于1.0的值开始(在z = 0)。这是因为表面下的下流光不仅包括那些刚刚穿过表面的光子(这些光子的fid = 1.0),还包括那些属于上升流的光子,以及那些刚刚从表面向下反射回来的光子。这些光子的fid远小于1.0,因此,尽管它们只占总数的一小部分,但它们使fid的平均值显著低于1.0。
对于非垂直角度入射到表面的光,其行为与垂直入射的光大致相同,只是表面以下的fi和fid值较低,而光
图6.15美国Pend Oreille湖4.24m深度上升流光辐射度分布矢量图。泰勒(1960)的辐射测量在所有方位角上的平均值。辐射矢量在最低点角间隔为10°。
图6.15美国Pend Oreille湖4.24m深度上升流光辐射度分布矢量图。泰勒(1960)的辐射测量在所有方位角上的平均值。辐射矢量在最低点角间隔为10°。
场在较浅的深度处达到渐近状态:比较0 = 0°和0 = 45°的曲线。在非垂直入射光束的情况下,应该认识到,尽管在zeu的各个方位上的平均角度分布几乎已经稳定到它的最终形式,但太阳垂直平面上向下的辐射度分布仍然明显不同于渐近分布:这可以在图6.11a中29m (zeu«28 m)的曲线中看到。
上升流的角度分布是在地表以下很短的距离内形成的。在美国的Pend Oreille湖,在4.2和i^o ^ TOO之间的所有深度,变化仅在0.37到0.34之间
66.1米。蒙特卡罗计算表明,对于b/a值在0.1至20之间的水域,通常在0.35至0.42之间真光区.上升流应该具有这些特征并不奇怪,因为它主要由反向散射光组成:反向散射不随角度发生强烈变化,因此无论向下辐射分布如何,都会产生相当相似的向上辐射分布。
Pend Oreille湖中上涌光流在水面附近的辐射度分布如图6.15所示为极坐标图。如果,正如有时假设的那样(见§6.4),上升流通量具有与朗伯反射器上方相同的辐亮度分布(所有角度的辐亮度相同),则图6.15中的所有辐亮度向量将具有相同的长度。从数据中可以清楚地看出,向上辐射度分布与兰伯分布相差甚远。
从角度分布随深度的变化可以预期,辐照度反射率随深度的增加而增加,但在ft和ftd趋于最终值的同时趋于稳定(图6.14)。因此,在自然水体中,通过确定辐照度反射率值在什么深度停止增加,可以找到建立渐近辐照度分布(在所有方位角上的平均值)的深度。
继续阅读:辐照度的垂直衰减
这篇文章有用吗?
