粒子散射
瑞利和爱因斯坦-斯摩鲁乔斯基散射理论只适用于散射中心相对于光的波长较小的情况:在气体分子和纯液体的微小密度波动的情况下是如此。然而,从光学上讲,即使是最原始的自然水域也不是纯净的,它们总是含有高浓度的颗粒——来自陆地或底部沉积物的矿物颗粒、浮游植物、细菌、死细胞和细胞碎片等——所有这些都会散射光线。自然水体中出现的颗粒具有连续的大小分布,大致为双曲线,54即直径大于D的颗粒数量与1/Dg成正比,其中g是特定水体的常数,但在不同水体中变化很大,从0.7到6虽然双曲线分布意味着较小的颗粒比较大的颗粒多,但在自然水域中,光所遇到的大部分颗粒横截面积是由于直径大于2毫米(636)的颗粒,相对于可见光的波长并不小,因此必须预期与密度波动类型不同的散射行为。较小的粒子虽然数量众多,但散射效率较低。
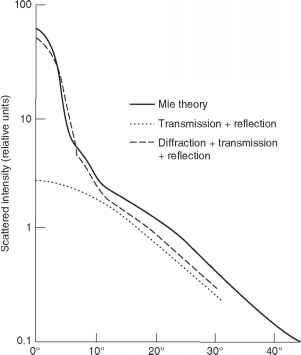
一个理论基础用于预测任何大小的球形粒子的光散射行为是由Mie(1908)提出的。该理论的物理基础类似于瑞利的理论,因为它考虑了在一个可极化体内由微波引起的振荡入射光场和光重新辐射(即散射)从身体作为这些振荡的结果。与瑞利理论不同的是,米氏理论将粒子等同于单个偶极子,而是考虑了粒子内部一系列电和磁多极子的附加贡献。米氏理论的优势在于它包罗万象——例如,对于非常小的粒子,它能得出与瑞利理论相同的预测;缺点是解析表达式比较复杂,不便于数值计算。对于大于光波长的粒子,米氏理论预测大多数的散射是在与梁轴成小角度的方向上(图4.1)。随着散射角的增加,一系列的极大值和极小值被预测出来,但是当存在不同粒径的混合物时,这些极大值和极小值就被平滑了。
对于大于几个波长的光的粒子,可以在衍射和几何光学的基础上得到对散射机制的合理理解,而不必求助于电磁理论。当一个物体被平面光波照射时,物体在它后面屏幕上的阴影并不是很精确地定义的:就在它的外面会出现一系列同心的微弱暗带;而较轻的同心圆带,其中明显有一些光线落下来,将出现在几何阴影的区域内。这种现象——衍射——是由于来自被照亮物体边缘不同点的部分波之间的干涉(在暗环中是破坏性的,在亮环中是构造性的),同时到达屏幕上特定点但不相(因为穿过的距离不同)。在圆形物体的情况下,叠加在圆形阴影上,在中心有一个亮点,周围是交替的暗和光环。事实上,大部分被粒子衍射的光在与光束初始方向的一个小角度内向前传播(产生亮点)。随着与轴的角距离的增加,衍射强度经历了一系列的最小值和最大值(暗环和光环),它们在高度上逐渐减小。
将几何光学应用于这些较大的粒子,可以很容易地看出,一些光将在外表面反射,一些将通过粒子并发生折射,或内部反射以及折射(图4.2)。在所有情况下都是光子
散射角
图4.1根据Mie理论(Ashley and Cobb, 1958)或根据透射和反射,或衍射、透射和反射(Hod-kinson and Greenleaves, 1963)计算的透明球散射强度角分布。粒子有一个折射率(相对于周围介质)为1.20,直径为光波长的5到12倍。源自Hodkinson和Greenleaves(1963)。
散射角
图4.1根据Mie理论(Ashley and Cobb, 1958)或根据透射和反射,或衍射、透射和反射(Hod-kinson and Greenleaves, 1963)计算的透明球散射强度角分布。这些粒子的折射率(相对于周围介质)为1.20,直径是光波长的5到12倍。源自Hodkinson和Greenleaves(1963)。
被卷入的物体将会偏离它们最初的方向,即会被分散。通过这些机制散射的光仍然主要是正向的:散射强度随着角度的增大而不断减小,但在小角度时,散射的集中程度与衍射引起的散射不同。Hod-kinson和Greenleaves(1963)对混合大小的球形颗粒悬浮液的计算表明,小角度(高达约10°至15°)的大多数散射可归因于衍射,而大角度的大多数散射是由于外部反射和折射透射(图4.1)。在衍射和几何光学的基础上计算的散射角变化比较接近
外r^lKlrßrl

图4.2粒子对光的散射:反射和折射过程。
内部rflf | K;吨
Hihu ^ tiun
图4.2粒子对光的散射:反射和折射过程。
由米氏电磁理论推导出来的。之所以存在这样的差异,很大程度上可能是由于透射光通过折射率较高的介质时引起相变,在衍射光和透射光之间产生了额外的干涉效应。这种现象被称为异常衍射。
光束中的任何粒子都会散射光束的一定比例,散射的辐射通量将等价于入射光束的一定截面积内的辐射通量。这个面积是粒子的散射截面。散射效率因子Qscat是散射截面除以粒子的几何横截面积(对于半径为r的球形粒子pr2)。同样,对于吸收粒子,吸收的辐射通量相当于入射光束的一定横截面积:该面积为吸收截面粒子的。吸收效率因子,Qabs,是吸收横截面除以粒子的几何横截面积。衰减的效率因子Qatt (吸收和散射组合)因此由
一个粒子的衰减效率可以大于1:也就是说,一个粒子可以影响入射光束中更多光的行为,而不是它的几何截面所拦截的光。这可以分别适用于吸收和散射:也就是说,粒子吸收或散射的光可能超过其几何截面所拦截的光。在电磁理论方面,我们可以说粒子可以扰动远远超出其自身物理边界的电磁场。以电磁学为基础的米氏理论可用于
Qatt - Qscatt + Qabs

0.0 1.5 3.0 4.5 6.0 7.5 9.0 10.5颗粒直径(嗯)
图4.3非吸收球形粒子的散射效率随尺寸的变化关系。粒子相对于水的折射率为1.17。波长= 550 nm。连续线,单个粒子的Qscatt,使用Van de Hulst(1957)方程计算-见正文。折线,含1g颗粒m-3的悬浮液的散射系数(b)。
0.0 1.5 3.0 4.5 6.0 7.5 9.0 10.5颗粒直径(um)
图4.3非吸收球形粒子的散射效率随尺寸的变化关系。粒子相对于水的折射率为1.17。波长= 550 nm。连续线,单个粒子的Qscatt,使用Van de Hulst(1957)方程计算-见正文。折线,含1g颗粒m-3的悬浮液的散射系数(b)。
计算粒子的吸收和散射效率。van de Hulst(1957)更简单的反常衍射理论也可以用来计算折射率高达周围介质折射率两倍的粒子的散射效率。关系是
4个4
其中p = (4na/X)(m- 1), m是粒子相对于周围介质的折射率,a是粒子的半径。对于非吸收粒子,Qscatt = Qatt。图4.3显示了相对于水的折射率为1.17(自然水中无机颗粒的典型值)的球形非吸收颗粒对绿光的散射效率随颗粒大小的变化方式。可以看出,在直径为1.6 mm时,散射效率从非常小的粒子的非常低的值急剧上升到约3.2。随着直径的增加,它首先减小,然后再次增加,并经历一系列振幅减小的振荡,直到非常大的粒子的Qscatt值为2.0。在光合作用范围内的任何波长的自然水中所发现的任何类型的散射粒子,都可以表现出Qscatt随大小变化的类似一般模式。
当直径减小到最佳散射以下时(例如,图4.3中从1.6 mm向下),单个颗粒的效率就会降低。然而,对于每单位体积的粒子质量给定,每单位体积的粒子数量必须随着粒子尺寸的减小而增加。因此,有兴趣确定粒子悬浮液的散射系数是如何固定的重量浓度随颗粒大小而变化。在黏土矿物浓度为1 gm~3的典型范围内,这种密度颗粒的计算结果如图4.3所示。正如预期的那样,由于颗粒数量的增加与直径的减小同时存在,用b表示的悬浮的总散射量并不像单颗粒散射效率那样随着直径的减小而急剧下降,并且悬浮散射的最佳颗粒直径(~1.1 mm)低于单颗粒散射的最佳颗粒直径(^1.6 mm)。随着颗粒直径的增加,超过了最佳值,因此悬浮液的散射逐渐减少到非常低的值,只有轻微的、严重阻尼的振荡,对应于单个颗粒的Qscatt中的振荡。707
继续阅读:梁大气透射表
这篇文章有用吗?