固有的光学特性
光子在水中只会发生两种情况:它们可以被吸收,也可以被散射。因此,如果我们要理解太阳辐射发生了什么当光线进入任何特定的水体时,我们需要测量水吸收和散射光线的程度。的吸收和散射对于任何给定波长的光,水介质的性质用吸收系数、散射系数和体积散射函数来规定。这些被Preisendorfer(1961)称为固有光学性质(IOP),因为它们的大小只取决于构成水生介质的物质,而不取决于可能弥漫在水中的光场的几何结构。它们是在一个想象的、极薄的平面平行介质层的帮助下定义的,平行的单色光束以直角照射(图1.4)。一些入射光被薄层吸收。一些是
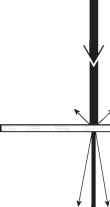
图1.4光束与水介质薄层的相互作用。在未被吸收的光中,大多数光在传输时没有偏离其原始路径:一些光被散射,主要是向前。
图1.4光束与水介质薄层的相互作用。在未被吸收的光中,大多数光在传输时没有偏离其原始路径:一些光被散射,主要是向前。
分散——也就是说,使其偏离原来的路径。被吸收的入射通量的分数除以层的厚度,即吸收系数a。被散射的入射通量的分数除以层的厚度,即散射系数b。
为了定量地表达这些定义,我们使用了吸收率A和散射率b。如果F0是平行光束形式入射到某个物理系统上的辐射通量(能量或单位时间的量子),Fa是系统吸收的辐射通量,Fb是系统散射的辐射通量。然后,即吸收率和散射率是辐射通量从入射光束损失的分数,分别通过吸收和散射。吸收和散射的总和被称为衰减,C:它是从入射光束损失的辐射通量的分数吸收和散射结合。在无穷小薄层,厚度Dr的情况下,我们分别表示吸收和散射损失的入射通量的非常小的部分DA和DB。然后
我们现在可以定义的另一个固有光学性质是光束衰减系数c。它由c - a + b(1.30)给出。
和是被吸收和散射的入射通量的百分比,除以层的厚度。如果将由于吸收和散射而损失的入射通量的极小部分结合起来,用符号DC表示(其中DC - DA + DB),则c - DC=Dr (1.31)
吸收系数、散射系数和光束衰减系数均以1/长度为单位,一般用m-1表示。
在现实世界中,我们无法在无限小的薄层上进行测量,因此,如果我们要确定a、b和c的值,我们需要将这些系数与有限厚度层的吸光度、散射度和光束衰减联系起来的表达式。考虑一种介质,用一束平行辐射通量F0的细光束垂直照射。当光束穿过时,由于吸收和散射而失去强度。现在考虑介质中厚度为Dr的无限小的薄层,在深度为r的地方,光束中的辐射通量减小到f。通过Dr时辐射通量的变化为DF。薄层的衰减为
(负号是必要的,因为DF必须是负的)
在0和r之间积分,得到ln -——cr (1.32) $0
表示辐射通量沿光束路径沿距离呈指数递减。式1.32可以改写为c = ^ln - (1.34)
因此,使用eqn 1.34或1.35,可以从平行光束通过已知路径长度的介质r的强度衰减测量中得到光束衰减系数c的值。
的理论基础用于测量吸收和散射系数就不那么简单了。在具有吸收而散射可忽略的介质中,a =-^ln(1 - a) (1.36)
r成立,在散射但吸收可以忽略的介质中,关系b =-^ln(1 - b) (1.37)
R是成立的,但在任何介质中,既吸收光又大量散射光,这两种关系都不成立。把这些方程应用于这样的介质,就很容易看出这一点。
在eqn 1.37的情况下,在有机会散射之前,一些测量光束将在路径长度r内被吸收除去,因此散射光量B将低于满足方程所需的光量。同样,A的值将低于满足eqn 1.36所需的值,因为在有机会被吸收之前,一些光将通过散射从测量光束中移除。
为了实际测量a或b,必须避开这些问题。在吸收系数的情况下,可以安排从测量光束散射的大部分光仍然通过大约相同的介质路径长度并被检测系统收集。因此,散射对总衰减的贡献很小,可以使用eqn 1.36。在散射系数的情况下,没有仪器方法可以避免吸收造成的损失,因此必须单独确定吸收,并对散射数据进行适当的修正。我们将在后面更详细地考虑测量a和b的方法(§3.2和4.2)。
散射影响光穿透介质的方式不仅取决于散射系数的值,而且还取决于初级散射过程产生的散射通量的角度分布。这种角度分布对于任何给定的介质都有一个特征形状,并由体积散射函数b(0)指定。这被定义为一个体积元件在给定方向上的辐射强度,平行光束照射下的dV,在体积横截面上的每单位辐照度,每单位体积(图1.5a)。定义通常用数学形式表示
由于,从§1.3的定义
其中dF(0)为与光束成0角的实心角do单元中的辐射通量,F0为入射在横截面积dS上的通量,由于dV = dS。是体积元的厚度,那么我们可以这样写
体散射函数的单位为m_1 sr_1。
平行光束通过薄介质层时,光散射沿光束方向呈径向对称。因此,以0角散射的光应该被认为是一个半角为0的圆锥体,而不是一束光(图1.5b)。
由eqn 1.39可知,b(0)是在介质中每单位路径长度上沿0方向散射的单位立体角辐射通量,表示为入射通量的比例。角区间0到0 +D0对应于一个实角元素等于2p sin0 D0(图1.5b),因此在这个角区间内散射的入射辐射通量(每单位路径长度)的比例为b(0) 2p sin0 D0。为了得到散射在dV中的入射通量的比例,
继续阅读:光学深度
这篇文章有用吗?