向上的辐照度和光辉

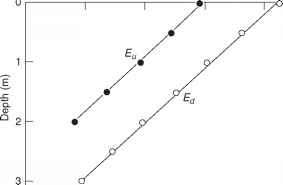
由于在水中的散射，在任何深度，只要有向下的通量，就会有向上的通量。这总是比向下的通量小，通常比向下的通量小得多，但在散射与吸收的高比下，可以显著地贡献用于光合作用的总光。此外，在任何水域中，上涌光对海洋的遥感都是至关重要的水生环境(第7章)，因为它是向上的通量穿透表面的那部分，被探测到远程传感器．在任何深度，向上的通量可以看作是在同一深度的任何一点向下的通量中向上散射的那一部分，在被吸收或向下散射之前成功地再次渗透到该深度。因此，我们可以期望向上通量的辐照度与向下通量的辐照度密切相关;这是被发现的情况。图6.6显示了在澳大利亚的一个湖泊中，PAR的向上和向下辐照度随深度平行递减。向下的辐照度随太阳高度或云量的变化而变化，也会伴随向上辐照度的相应变化。考虑到向上辐照度与向下辐照度密切相关，可以方便地考虑水的光学性质对上升流通量可能产生的任何影响，即它们对上升流与向下辐照度之比Eu/Ed的影响，即辐照度反射率R。

量子辐照度(^爱因斯坦m2 s 1) 1 10 100 1000 10 000

量子辐照度(^爱因斯坦m2 s 1) 1 10 100 1000 10 000

量子辐照度(1018量子m-2 s-1)

图6.6澳大利亚湖泊PAR辐照度随深度的上升(•)和下降(o)平行衰减(Burley Griffin, ACT)(在Kirk, 1977a之后)。

量子辐照度(1018量子m-2 s-1)

图6.6澳大利亚湖泊PAR辐照度随深度的上升(•)和下降(o)平行衰减(Burley Griffin, ACT)(在Kirk, 1977a之后)。

向上的光通量中有一小部分来自于向下的光以大角度向前散射，这些光已经以一定的角距离从垂直方向传播。随着太阳高度的降低，水中的太阳光束变得不那么垂直，源于前向散射的那部分向上通量就会增加。体积散射函数的形状是这样的，这不仅抵消了一个事实，即增加的反向散射通量的比例现在是向下的。净结果是辐照度反射率随着太阳高度的降低而增加，但影响不是很大。在印度洋，随着太阳高度从80°.636降低到31°.636,10 m深度450 nm光的R从5.2增加到7.0%对于澳大利亚的Burley Griffin湖，地表下整个光合波段(400-700 nm)的辐照度反射率从太阳高度75°时的4.6%增加到太阳高度27°时的7.9%。但是，在1米处，在这混浊的水中，光场正接近于渐近状态(参看§6.6)，R只从7.4增加到8.6%

虽然，正如我们所看到的，有一个贡献来自前向散射，大部分上升流通量起源于后向散射。因此，我们可以期望R与所讨论的水的后向散射系数bb大致成正比。当向上散射的光子从散射点向上移动到测量点时，它们的数量因吸收而逐渐减少，而更不频繁的是，由于进一步的后向散射，它们再次向下定向。因此，我们可以期望反射率将与水的吸收系数a成反比变化。我们还可以期望，反射率随后向散射而增加的主要趋势将在某种程度上减少，因为后向散射对向上通量的减少的贡献。

通过对水下光场的数学建模，探索了辐照度反射率随介质固有光学特性变化的实际方式。辐射转移理论的简化版本339,956得出结论，对于介质(如大多数天然水)，R与bb/(A + bb)成正比，其中bb«A。这是一种可以根据上面所概述的定性依据来预期的关系。事实上，由于bb通常比a小得多，我们可以期望在一个合理的近似值中，R应该与bb/a成正比。通过蒙特卡罗和其他方法对各种光学类型的水的水下光场进行数值模拟，484,702,1091揭示了这确实是事实，我们可以写下来

其中R(0)是地表下的辐照度反射率。比例常数C(m0)本身是太阳高度的函数，我们可以用m0表示，即表面以下折射太阳光束的天顶角余弦。对于任何给定的水体，反射率随着太阳高度的降低而增加，478,484,706,949即C(m0)随着m0的降低而增加，并且确实可以表示为(1- m0)，706,712 1/m0,640或[(1/m0) - 1)]，478的近似线性函数，例如，如下的关系

其中C(1.0)是C(m0)的值天顶的太阳(m0 = 1.0)， M是由散射相形状决定的系数

AfJQ 710

函数。，对于天顶太阳，eqn 6.3中的比例常数，即C(1.0)，大约等于0.33484702,1091，对于具有大范围散射相函数的水也是如此在海洋遥感领域中，eqn 6.3中辐照度反射率与bb/a的比例常数C(m0)通常用符号f表示，这表明f本身是太阳高度和散射相位函数的函数。因此

对于任何给定的海洋位置，可以从eqn 6.4中获得f (= C[m0])的一个近似但现实的估计，使用太阳天顶角，并从先前公布的一系列水类型中选择一个合理的M值Hirata和Hojerslev(2008)利用辐射转移理论，并应用某些近似，表明对于吸收系数在数值上远大于后向散射系数的水域和波段(即不包括透明海水中的紫蓝色波长)，比例常数f是表面以下光场平均向下余弦的近似函数(主要由太阳角)，后向散射的平均余弦，gb，按照gb - 0.0849

F fidgb + 0.8585 (.)

Morel和Prieur(1977)比较了他们对各种海洋和沿海水域的光合光谱R的测量值与用eqn 6.3计算的值。对于清澈的蓝色海域，R的光谱分布曲线与实测曲线吻合较好。对于浮游植物含量高的上升流海水和浑浊的沿海水域，在400 - 600 nm处的一致性是令人满意的，但在某些情况下，在较长的波长处不太好。生产水域的部分问题是上升流通量中在685 nm处出现叶绿素荧光发射峰值(见§7.5)，这使该区域的观测反射率高于计算值。在波长大于580 nm时，虚假的高反射率值也是由拉曼发射引起的。

在地表以下的上升流通量中，近似垂直向上的那部分对遥感有特别重要的意义。在垂直向上方向上的亚表面亮度，我们将称为Lu。上升流通量的角度分布在0 ~ 20°范围内，向上辐射度随最低点角的变化不大。因此，在这个范围内的Lu(0)的测量值，或者超过这个范围的平均值，都可以作为Lu的合理估计值。Lu和Eu一样，对于给定的水，与Ed平行变化，我们将把Lu/Ed的比值称为辐度反射率。在遥感的背景下，它通常被称为地下遥感反射率，rrs。

Q是向上辐照度与最低点辐照度的比值

一些遥感辐射计具有非常广阔的视场:在SeaWiFS例如扫描仪(§7.1)，它是±58.3°。虽然由于表面的折射，水下的角度范围较小，但一些远距离测量的辐亮度值将与远离最低点的水下辐亮度值相对应。认识到这一事实，Morel和Gentili(1993,1996)定义了另一个版本的Q，作为天顶太阳角(00)的函数，考虑的辐射方向的最低点角(0')，以及辐射垂直平面与太阳平面之间的方位差(f)。

«*•'•af) = MOT) (6-10)

对于地表下的辐照度反射率，他们使用符号R(00)来表示它与太阳天顶角的关系。

照度反射率的值，就像辐照度的值一样，是水固有光学特性的函数。给定Eu/Ed与固有光学性质之间的关系，例如eqns 6.3和6.4中所体现的关系，如果我们知道Eu与Lu的比值Q，我们可以将Lu/Ed(即rrs)与bb和a联系起来

r " = - q - (6.11)

简化的假设通常是上升流通量的辐射度分布与兰伯反射器上方的辐射度分布相同(所有角度的辐射度值相同)。如果是这样的话，那么比值Eu/Lu将等于p。事实上，辐射度分布不是朗伯式的(见§6.6和图6.13)，在Pend Oreille湖在太阳高度57°1380处的测量表明，在这个水体的表面附近，Q等于5.08蒙特卡罗模型计算(Kirk，未发表)

在太阳高度为45°的海面下，b/a值在1.0到5.0之间的水域的Q值约为4.9。因此，对于中等太阳高度，我们可以合理地假设Eu/Lu«5。对于b/a值在1.0到5.0范围内的水域，蒙特卡罗计算得到的值为^0.083。

Aas和Hojerslev(1999)提供的数据显示Q是5米深处太阳高度(hs°)的函数，该数据基于对地中海西部70个站点角辐射分布的测量。Q随着太阳高度的增加而降低，从hs ~ 0°的^5.2下降到hs ~ 90°的^3.4。这种关系可以近似地表示为

Q =(5.33±0.30)exp(-(0.45±0.08)罪hs) (6.13)

与西格尔(1984)早先提出的观点一致

大西洋中部的清澈海水Aas和Hojerslev认为，这种关系(eqns 6.13和6.14本质上是相同的)可能对接近表面的清澈海水普遍有效。

Loisel和Morel(2001)使用计算机模拟(Hydrolight)来描述情况2中向上辐射场偏离各向同性的程度(参见§3.4关于该术语的解释)。在以沉积物为主的浑浊水体中，随着太阳高度从90°降低到15°，Q从3.53逐渐增加到4.09。在更清澈、以黄色为主的水中，在相同的太阳角度范围内，Q从3.69增加到5.02。对于最低点辐亮度，函数f/Q (eqns 6.11, 6.12)规定了地下遥感反射率对bb/a的依赖关系，它与太阳角度没有显著的依赖关系，在两种水的角度范围内都相当接近0.08。然而，对于极底角-35°的辐射，对应于水面以上50°，f/Q依赖于太阳角度，随着太阳高度从90°下降到15°，在混浊水中从0.085下降到0.129，在彩色水中从0.069下降到0.123而增加。

在海洋遥感中，它是Rrs，地表以上辐射度反射率-垂直向上的留水辐射度(Lw)除以Ed(0+)，地表以上向下的辐照度

这在第一个实例中是确定的(我们在这里采用的约定是，0+对应于表面以上的任何点，而0-表示表面以下的零深度)。从这一步到亚表面辐亮度反射率，我们从n2得到亚表面辐亮度

Lu(0-， 9'， f) = - Lw(0, f) (6.16)

式中0为辐亮度的上水面天顶角，0′为水中相应的折射最低点角，f为方位角，n为折射率， [1 - p(0'， 0)]是在水气界面处的菲涅耳反射，在最低点角0'491,951处的辐射。由于地表反射，入射的太阳通量在地表下略微降低了向下的辐照度

Ed(0-)0 = Ed(0+)(1 - p) (6.17)

其中Ed(0-)0是在零深度向下的辐照度，这是由刚刚穿透表面的太阳辐射产生的，p是整个水面的菲涅耳反射，太阳+天空，入射太阳通量。

在零深度处向下的总辐照度Ed(0-)略大于Ed(0-)0，因为在表面穿透通量之外，还增加了在水-空气界面向下反射的那部分上升流通量。为了估计这额外的辐照度，我们可以考虑初始向下的通量，由于水柱内向上散射的结果，上升到辐照度Ed(0-)0 R的向上通量，其中R是辐照度反射率，R = Eu/Ed。部分向上的通量在水-空气界面处进行向下反射，产生新的具有辐照度的向下通量Ed(0)0Rr，其中r是整个漫射上涌辐射流的水-空气菲涅耳反射，其值为-0.48。这个新的向下的通量反过来，由于向上散射，接着是内表面反射，产生第二个额外的向下通量，辐照度Ed(0)0(Rr)2。这样就产生了一个无穷级数的向下递减的通量

Ed (0-) = Ed (0-)0[1 + Rr + (Rr)2 + (Rr)3 +…(Rr) +…

求和得到什么

对于地下遥感反射率，Lu(0)/Ed(0)，可写成

在eqn 6.20中，留水亮度Lw(6, f)和表面入射辐照度Ed(0+)是实验确定的输入参数;折射率n是已知的(-1.34);可以计算菲涅耳反射率p和p;由于海水中的R通常<0.1,R为- 0.48，因此(1 - Rr)项无论如何都接近1.0，如果在海洋区域插入一个合理的R值，就可以估计出来。因此，对于遥感场景的每个像素，都可以获得与水固有光学特性直接相关的地下遥感反射率(rrs)(见第7章)。

上升流通量的谱分布一定部分地依赖于下升流通量的谱分布，但是，正如eqns 6.3和6.5所示，它也显著地受到整个谱上bb与a之比变化的影响。例如，在清澈的海水中，在光合光谱的蓝色(400 nm)端，R可高达10%，在那里纯水吸收较弱，但后向散射相对较强(见§4.3)，而在红色(700 nm)端，R可低至0.1%，水吸收较强图6.7显示了透明海水和内陆地区向上辐照度和辐照度反射率的光谱分布蓄水．海水的上升流通量主要由400 ~ 500 nm波段的蓝光组成。在浮游植物含量高的生产性海水中，光合色素吸收了大量上涌的蓝光，因此上涌通量的峰值移到绿色的565至570纳米由于浮游植物叶绿素的荧光发射，在685 nm处也有一个峰。在内陆水域(图6.7b)，黄色物质和浮游植物吸收了大部分蓝光和宽频带，在580 nm左右达到峰值，占了大部分量子

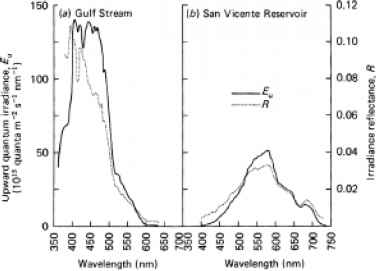
图6.7海洋和内陆水域向上辐照度和辐照度反射率的光谱分布(根据Tyler和Smith, 1970年的数据绘制)。(a)巴哈马群岛外5米深的墨西哥湾流(大西洋)。(b)美国加利福尼亚州圣地亚哥San Vicente水库，深度1米。

在480和650 nm之间可以观察到:在这条曲线中可以看到大约680 nm处的叶绿素荧光发射。

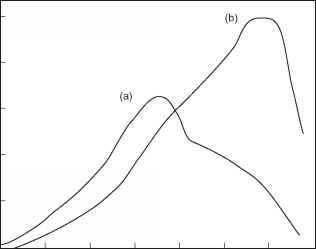
在到达地表的上升流光通量中，约有一半再次向下反射，其余的通过水-空气界面产生涌现通量(§7.2)。正是这种通量，以不同的比例与入射光反射在水面上，这是由观察水体的人类观察者所看到的，其强度和光谱分布在很大程度上决定了水体的视觉/美学质量。图6.8显示了澳大利亚一个湖泊地表下上升流通量的光谱分布，该湖泊时而呈清澈的绿色外观，时而呈浑浊的棕色外观。在第一种情况下，光谱分布在大约575 nm的黄绿色区域达到峰值，这是由于在光谱的蓝色端被中等水平的腐殖质物质吸收，在红色端被水本身吸收。在第二种情况下，由于悬浮土壤颗粒的强烈散射，上升流通量具有更大的总辐照度，在红色区域的675至700 nm处有一个峰值，这是由于高浓度可溶性和颗粒腐殖质物质在蓝色和绿色区域的强烈吸收。河流

波长(nm)

图6.8澳大利亚首都地区Gin-ninderra湖地表下向上辐照度光谱分布。(a) 1983年4月20日。外观-清澈，绿色。B - 3.2米。A440 - 1.22米。(b) 1984年8月15日。外观:浑浊，棕色。B - 28.2 m-1。A440 - 23.1m-1。

波长(nm)

图6.8澳大利亚首都地区Gin-ninderra湖地表下向上辐照度光谱分布。(a) 1983年4月20日。外观-清澈，绿色。B - 3.2米。A440 - 1.22米。(b) 1984年8月15日。外观:浑浊，棕色。B - 28.2 m-1。A440 - 23.1m-1。

由于含有高浓度的矿物颗粒(“冰川粉”)，但有机物质很少，从冰川中提取的冰粉呈乳白色或灰色。

水体的表观颜色是由观测者接收到的通量的色度坐标决定的，这些色度坐标可以使用CIE(国际照明委员会)标准比色系统从光谱分布中计算出来(详情见Jerlov, 1976)。davis - colley等人(1988)利用新西兰14个湖泊的上涌光谱分布数据进行了这样的计算，并提出这对于关心他们所负责的水体美学质量的水资源管理者来说是一个潜在的有用工具。davis - colley, Vant和Smith(2003)的书中对人类使用自然水体的颜色和清晰度进行了全面的处理。

在Tyler和Smith(1970)研究的海水中，5 m深度总PAR的辐照度反射率在约2%至5%之间变化。用于轻微或非常浑浊内陆水体在澳大利亚东南部，地表以下PAR的辐射反射率值通常在4%至10%之间，但也观察到低至2%至19%的值，较高的值与较高的浑浊度有关。697,700反射率值随深度的增加而有所增加(见§6.6)，到目前为止观测到的最大值约为24%。在散射低，但由于可溶性黄色物质浓度高，颜色强烈的内陆水域，PAR的反射率可能非常低。在塔斯马尼亚的一系列这种类型的湖泊中，PAR在地表以下的辐照度反射率范围从约1.2%下降到0.14%

在球石藻大量生长的地方，海洋的反射率大大增加。球石藻是一种细胞被高度分散的钙质鳞片所覆盖的触藻(球石藻，图4.10)。在缅因州湾的一次球石藻爆发中，Balch等人(1991)在一个站测量了蓝绿波段的地下反射率值为5%至7%，在另一个站测量了22至39%。高反射率值似乎主要是由于大量分离的可可石悬浮在水中，而不是整个细胞。

在无色的清澈海水中，主要为蓝绿色的下行光流的拉曼散射，由于相关的波长向较长的转移(见§§4.2,7.5)，导致520至700 nm范围内的微弱漫射散射光场。869,1291,1321虽然这对光合初级生产不太重要，并且对下行光场的贡献也很小，但它对的下部区域的上涌光流却有显著的贡献真光区，这可能是在较深处反射率异常增加的原因，有时也观察到这种现象。

在足够浅的水体中，大量的光可以到达底部，除非底部颜色非常深，否则由于底部的反射，靠近底部的Eu会增加。

继续阅读:水下光场的角分布

这篇文章有用吗?

＋1 0