热收支方程
北极帽的热收支可以近似地表示为:
式(3.3)指出,北极大气中湿静态能(在引言中定义)的储存时间变化AE/At用的和表示
Frad
F墙\25mb
Frad v
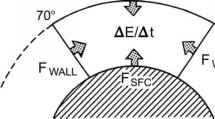
图3.5北极帽的能量平衡示意图(来自Nakamura和Oort, 1988年,经AGU许可)。
F墙\25mb
大气顶部的净辐射(Frad),在北纬70°从表面延伸到大气顶部的假想墙(Fwall)上的向极地的净能量通量净热通量在地球表面(Fsfc)如果右边三项之和为正,则大气获得能量。如果它们的和是负的,大气就会损失能量。所有单位都在wm -2。图3.5提供了该问题的示意图。我们从式(3.3)中提出的基本问题是:进入极帽两侧、顶部和底部的净能量通量的相对贡献是什么?这些能量通量如何随季节变化而引起大气能量含量的变化?通过回答这个问题,我们可以了解北极是如何运作的。这里描述的类似方法可用于编制全球能源预算的网格场,如Trenberth et al.(2001)所做的那样。首先考虑给定时间内大气的湿静态能量含量E。这表示为:
右边的项分别以内能(感热含量)、潜热和势能的形式表示大气的能量含量。这里,CP是恒压(1005.7 J K-1Kg-1)下的大气比热,T是温度(开尔文),L是蒸发潜热(2.5 × 106 J kg-1), q为比湿(g kg-1), g为重力加速度(9.8 m s-2), z为位势高度(流量)。因此,湿静能随着温度的升高、水分含量的升高和位势的升高而增加(gz = $)。位势表示将单位质量从海平面提升到z高度所需要的功:位势越大,势能就越大。
括号中的三项的单位都是焦耳/千克(jkg -1),即每单位质量的能量。术语gz有更明显的单位m2 - s-2。然而,能量(J)的单位是kg m2 s-2。重新排列m2,代入m2 - s-2,得到所需的单位J kg-1。极冠的总能量含量E的单位是焦耳,通过对体积(dV)积分得到。请注意,在垂直维度上,从大气表面延伸到大气顶部,必须有一个质量加权,通过dp/g(单位为kg m-2)的积分来实现,其中p是压力。
Nakamura和Oort(1988)从10年的数据集中获得了E的月平均值地球物理流体动力学实验室(GFDL),主要基于罗文探空数据,并扩展到25 hPa水平(因此包含大部分大气质量)。AE/At的月值由相邻月份E的差异来确定。例如,5月E大于4月,因此5月AE/At为正值。以焦耳/单位时间为单位的结果值,除以极帽的面积,得到最终所需的单位W m-2。
Frad,大气顶部的净辐射,可以分解为:
Fsw是区域平均向下TOA短波(太阳)通量,它随太阳赤纬而季节性变化。A是地球极盖的面积平均反照率地球大气层系统(即行星反照率),所讨论的系统取决于地表反照率、云量和晴空散射和吸收。流是由大气和地表发射到太空的长波辐射。Nakamura和Oort(1988)基于1966年至1977年间地球轨道卫星测量的反射太阳和发射长波通量的Frad。
Fwall表示湿静态能量进入极帽的净水平输送,可以分解为:
íwaii = JJCp[vT]dx dp/g + JJL[vq]dx dp/g + JJg[vz]dx dp/g (3.6)
其中,横线表示时间平均值,方括号[]表示纬向平均值。右边的三项是:(1)感热,(2)潜热,(3)势能的通量。如果它们的和是正的(进入柱两侧的能量比离开柱的能量多),总通量就是正的。项[vT]是经向时间平均的纬向平均值温度变化,其中v为风的经向(南北)分量。乘以cp,得到纬向平均、时间平均经向感热通量。这个纬向平均项是在从地表到大气顶部的压力水平上评估的。然后在70°N (dx, x为单位距离)附近对每一层的纬向平均值进行积分。然后对每一层的积分进行垂直积分(dp/g)。同样地,经向潜热通量是由潜热的时间平均、纬向平均输送的水平和垂直积分计算出来的。最后,由经向风和位势高度的时间平均积的纬向平均值得到势能通量。Nakamura和Oort(1988)用10年GFDL数据集评估了Fwall及其组成部分。
式(3.3)中的最后一项是净表面通量。这是大气柱(以70°N为界)和从地表向下穿过陆地和海洋的柱(同样以70°N为界)之间的净热传递。我们可以把后者称为ocean-ice土地列。请注意,极地帽72%的表面积被海洋覆盖。孤立地考虑,热量从海洋-冰盖柱向大气柱的净传递意味着大气柱获得热量,而海洋-冰盖柱损失等量的热量。相反,如果热量从大气柱向海洋-冰-陆柱净传递,则大气柱损失热量,而海洋-冰-陆柱获得等量的热量。因此,这个术语表示净蓄水池(或体积)交换。净表面热通量不应与表面界面的能量收支相混淆(第5章),两者之和必须始终为零。在缺乏可靠地表数据的情况下,Nakamura和Oort(1988)将地表净热通量作为式(3.3)中其他项的残差。
在继续之前,有必要对湿静能(式(3.4))及其变化(式(3.3)进行一些澄清。潮湿的静态能量不是大气的总能量含量。它不包括大气中以液体或固体形式存在的水质量的少量显热含量(在云中或以雨或雪的形式从大气中落下),也不包括动能(运动的能量)。然而,由于这些术语的时间变化通常相当小,我们可以忽略它们。此外,湿静态能的定义,认为水的液相是零潜热状态。就"记帐"而言,这意味着,孤立地考虑,与聚变有关的向大气柱释放的热量(3.34 x105 Jkg-1)将被计算为到地表的负潜热通量(作为降雪)。这一效应将反过来算作从海洋-海冰-陆地柱进入大气柱的净表面通量。
为帮助进一步阐明净表面通量,有必要提出类似于式3.3的海洋-冰-陆柱能量收支的表达式:
左边的项是海洋-冰-陆地柱中热量的储存速率。右边的第一项,Fo,是向极地的净海洋热输送。跨越北纬70°的向极地(赤道)的海洋热净通量增加(减少)了海洋-冰-陆柱的热含量。Fi也是一种水平传递,表示潜热向极净通量,形式为雪和冰.正如第2章所介绍和第7章所扩展的那样,海冰(和覆盖的积雪)从极帽净流出到北大西洋。相同质量的冰在相同温度下的能量含量比相同质量的水低。假设输出的冰雪被替换为等效质量对于相同温度下的水来说,这种流出代表了海洋-冰-陆地柱的热量含量的有效增加。式(3.7)和式(3.3)通过相同的表面热流项联系起来。根据前面的讨论,显然,如果式(3.7)中的Fsfc是正的(从海洋-冰-陆柱进入大气柱的通量),这将导致海洋-冰-陆柱的热量损失,在式(3.3)中必须将其视为大气柱的热量增加。如果Fsfc in
式(3.7)为负,它导致大气柱的热量损失,与海洋-冰-陆地柱的热量增加相平衡。式(3.7)假设通过非海洋过程向柱的净水平换热可以忽略。它还假设圆柱延伸到足够的深度,这样我们就可以忽略热量传递到它的底部。
从长期年平均来看,式(3.7)中的储能变化(AE * /AT)为零。因此,年地表净热通量必须等于以Fo和Fi表示的海洋-冰-陆柱边界的热流。Naka-mura和Oort(1988)计算出(作为式(3.3)中其他项的残差)年平均表面通量为2.4 W m-2。Fi的估计值是根据每年3 x 1015公斤的北极冰流出量得出的。在北纬70°以北的地区,这相当于每年加热2.1 W m-2。重申前面的讨论,这假设输出的冰被相同数量和相同温度的水所取代。Vinje(2001)最近估计每年通过弗拉姆海峡流出的冰量约为2.6 x 1015 kgyr-1,对应约1.8 W m-2(假设所有的冰都没有融化就离开了极帽)。通过加拿大北极群岛航道的冰通量将是一个小的额外贡献。根据他们假设的年平均Fsfc为2.4 W m-2,年平均Fi为2.1 W m-2, Nakamura和Oort(1988)估计的Fo值仅为0.3 W m-2。小年平均值海洋热传输残差估计值与图3.3一致。Aagaard和Greisman(1975)估计,通过白令海峡和北大西洋(北纬65°)的海洋热输送分别约为0.002和0.14 PW。与图3.3中在北纬17°附近约为2 PW的最大值相比。
简单地说,Fsfc的年平均值较小并不意味着它在某个特定月份可以忽略不计。如图所示,某一个月的净地表通量可能与年平均值相差40倍以上。然而,Nakamura和Oort(1988)假设,虽然Fo和Fi在年平均意义上很小,但它们在全年中也很小,而且相对稳定。根据合理的近似,这两项可以从式(3.7)中删除,用于分析年周期。实际上,弗拉姆海峡平均冰输运有大约三个季节范围的因素(见第7章)。尽管Fi的假定稳定性质并不完全有效,但我们仍然得出这样的结论:虽然海冰输运对北冰洋的淡水收支极其重要(它代表主要汇),但它对海-冰-陆柱的热收支影响相对较小。
假设可以忽略向海-冰-陆柱的水平净换热,则地表净热通量可表示为:
Sm为潜热以冰雪形式储存的速率(S)。海冰的形成被认为是大气柱热量的增加和海洋-冰-陆地柱热量的相应损失。根据我们的惯例,降雪也有同样的作用。在这两种情况下,舒都是阴性的。如第五章和第七章所述,大多数海冰生长发生在现有冰的下面(在冰-海洋界面)。的释放热量通过冰的形成,然后向上传导到表面和柱外。如果SM是正的,这就意味着海冰和雪的表面融化,将海洋-冰-陆地柱的热量增加和大气柱的热量损失计算在内。海洋中感热的储存速度也是如此。如果这一项是正的,则海洋正在获得显热(温度上升),这代表着从大气中损失的热量。如果这项是负的,海洋失去热量,而大气获得热量。Sl是土地感热的储存率。陆地上感热的增加意味着地下热量的增加。由于这些热量本来可以用来提高大气温度,所以正的Sl对大气温度有负面影响大气的热量内容。当Sl为负时,相反的效果成立。Si为感热在雪中的储存率,其解释类似。
简化也是可能的,因为Sl和Si看起来相对较小(Nakamura和Oort, 1988)。因此,地表净热通量主要包含在海冰、积雪的生长和融化以及海洋显热储量的变化中。Nakamura和Oort(1988)能够根据Levitus(1984)对全球海洋热含量的分析来估计So的月值。通过对So和残差项Fsfc的估计,他们可以将Sm估计为另一个残差。
继续阅读:成分的季节性
这篇文章有用吗?