一个一个
溶质离子(B)则由式(DD): ifflB/MWB给出
(f ttr\ - mu)/MWA + imB/MWU
利用式(CC),由于每个溶解分子形成i个离子的mB克溶解盐而导致的蒸汽压降低由
因此,如果不挥发性溶质溶解在水中,水的蒸汽压降低的量与溶解溶质的摩尔分数成正比,考虑到发生的任何解离(vide infra)。应该注意的是,这假设理想溶液的行为。
正如我们在第九章中看到的,大气颗粒中有各种溶解的溶质,这将降低液滴的蒸汽压,相对于纯水。因此,人们对大气颗粒中水溶性物质的性质和比例及其大小分布非常感兴趣(例如,Eichel等人,1996年;Novakov和Corrigan, 1996;Hoffmann等人,1997)。因此,这种蒸汽压降低效应与开尔文效应的作用方向相反,开尔文效应会增加液滴上的蒸汽压。这两种效应结合在一起被称为Köhler曲线,它描述了大气中的气溶胶粒子在不同条件下是否会成长为云滴。
3.科勒曲线。计算一个水滴中溶解溶质的摩尔分数xn,需要知道水和溶解溶质的摩尔数。以双组分溶液为例,如NaCl溶于水,其中溶质解离成i离子(NaCl为i = 2)。假设将分子量为MWB的raB克盐溶解在水中,形成密度为ps的溶液,溶解离子的摩尔数为/mB/MWB。体积V = (4/3)7rr3的一滴水的摩尔数为[psV - mB]/MWA,其中MWA为水的分子量。溶解的摩尔分数
(t-n-rfo - mB)/MWA + /mB/MWB '
对于稀释溶液,当raB很小时,这可以还原为
RmWb P
其中b =[¿mBMWA/((4/3)irp8MWB)]。
溶质降低的蒸汽压与开尔文效应导致的蒸汽压增加同时作用,并抵消了这一作用[式(BB)]。将两者相乘,则含有溶解溶质的溶液上方蒸汽压的净结果为
应用近似
= 1 + x x /2!+•••,只使用前两项,Eq. (GG)变成
a = 2-yMWA/psi?T和r~4项已被省略,因为它相对于大气感兴趣半径的其他三个项较小。
术语过饱和,S,定义为(PA/PA - f),通常以过饱和百分比的形式表示,即100{PA/P°A - f),其中PA和PA的定义见方框14.2。液滴上的平衡蒸汽压与体积液体上的平衡蒸汽压[Eq. (HH)]之间的关系通常用过饱和表示为简化形式:
S对半径的曲线被称为Köhler曲线。如图f4.38a原理图这样的曲线。Reiss和Koper(1995)对Köhler曲线给出了更详细的热力学处理。
在云层中发现的典型过饱和值在0.2到2%之间。对于雾,数值要低大约一个数量级,通常在0.02到0.2%之间(Pruppacher和Klett, 1997)。
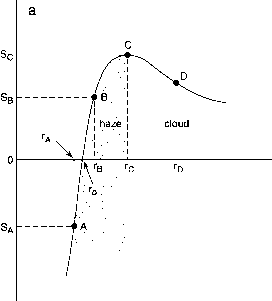
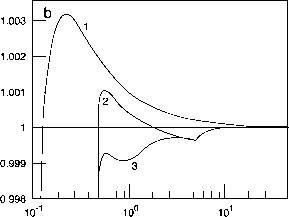
图14.38 (a)传统Köhler曲线示意图,S = PA/PX - 1为过饱和状态,r为液滴半径,(b) (NH4)2S04 30nm干颗粒Köhler曲线:(1)传统曲线;(2) 500 nm CaS04颗粒(微溶性)和(NH4)2S04与曲线1相同;(3)对于曲线2,但存在1ppb HNO,被粒子所占据(改编自Kulmala et al., 1997)。
图14.38 (a)传统Köhler曲线示意图,S = PA/PX - 1为过饱和状态,r为液滴半径,(b) (NH4)2S04 30nm干颗粒Köhler曲线:(1)传统曲线;(2) 500 nm CaS04颗粒(微溶性)和(NH4)2S04与曲线1相同;(3)对于曲线2,但存在1ppb HNO,被粒子所占据(改编自Kulmala et al., 1997)。
S与半径r的关系是这样的,在小半径时,由于蒸汽压降低,第二项占主导地位,S为负。在该区域,RH低于100%的空气与颗粒处于平衡状态;在大半径范围内,由于开尔文效应,第一项占主导地位,S变为正,最终达到最大值,然后再次下降。峰顶左边的区域被称为雾霾区,原因很快就会显现出来,而右边的区域被称为云滴区。
例如,在图14.38a中对应SA的水蒸气压下,一个给定质量(mu)的NaCl干颗粒被引入空气。假设RH在25℃时高于NaCl的潮解点~75%,颗粒会吸水溶解,形成半径为rA的稳定液滴。类似地,如果空气饱和与Su的比值增大时,颗粒在平衡条件下吸水并生长到半径ru。
然后,这些颗粒与空气中的水处于稳定的平衡状态。假设B点的粒子失去了一些水分子,开始收缩。小颗粒的平衡过饱和比原始颗粒低。然而,周围空气的过饱和程度仍然较高,因此水将凝结在颗粒上,使其恢复到原来的大小。类似地,如果B点的粒子获得了一些水分子,半径开始增加,保持这个新尺寸所需的S值将大于周围空气的S值,水将蒸发以恢复平衡尺寸。
简而言之,图14.38a中峰值左侧的粒子没有收缩或增长的趋势。因为它们一般在0.1- l-/j,m的大小范围内,可以有效地散射光线(见第9.A.4章),这些颗粒被称为雾霾颗粒或液滴。这些通常发生在相对湿度低于100%的情况下。
然而,考虑图14.38a中点D处的粒子。如果它得到了一些水分子,半径开始增大,周围空气的过饱和就会比这个更大的粒子所需的S平衡值更大。因此,水会凝结在液滴上,使液滴进一步生长。因此,位于峰值右侧的粒子处于不稳定的平衡状态(例如,见Reiss和Koper, 1995),因此可以从水的冷凝中活化成云滴。
关于气溶胶粒子对云性质的潜在间接影响,有两个问题:(1)新粒子的来源是什么?(2)这些新粒子如何生长到足够大的尺寸(>50 nm)来充当CCN?
第一个问题是新粒子的形成。如第九章所述。B,大气中气体成核形成新粒子的过程还不是很清楚。例如,观察到的H2S04的成核速率大大超过了计算的速率。在某些条件下边界层(BL)中新粒子形成的一个重要因素似乎是边界层与边界层之间的交换自由对流层(例如,Davison et al., 1996;Raes et al., 1997;Clarke et al., 1997)。例如,来自海洋的一些DMS可以被带到自由对流层,在那里它被氧化成硫酸盐,产生新的CCN。然后,将气团混合回BL中,可以在H2S04等低挥发性物质成核形成新颗粒之前,通过清除这些物质,抑制该区域新CCN的形成(例如,见Slinn, 1992;和Raes, 1995)。
第二个问题是,这些新粒子如何生长到足够大的尺寸,以充当CCN。粒子必须生长到充当CCN的尺寸由Köhler曲线在平衡条件下确定。Köhler曲线上S和r的峰值(图14.38)被称为临界值Sc.和rK(见问题6)。每当气团过饱和大于Sc时,就发生凝结形成云雾滴。然而,如果它小于Sc,粒子的半径小于临界半径rc。将保持平衡大小(例如,图14.38a中的B点),而不是形成云或雾。当然,在真实的大气中,有各种初始粒径,含有不同数量的溶解溶质,气团的过饱和也随时间而变化。然而,Köhler曲线为了解哪些粒子可以成长为云和雾,哪些不会提供了基础。
值得注意的是,Köhler关系假设是均衡的。然而,在真实的大气条件下,系统可能不处于平衡状态。P. Y. Chuang et al.(1997)和Hallberg et al.(1998)指出,如果云滴生长的时间尺度大于颗粒达到平衡的时间尺度,则CCN生长成云滴可能受动力学控制,而不是平衡。他们认为,忽视这种潜在的动力学限制可能会导致高估由给定数量的CCN形成的云滴数量。此外,使用云室的CCN测量技术可能无法准确评估环境条件下的CCN,因为在空气中遇到的时间尺度范围比测量中使用的时间尺度范围要大得多。目前,尚不清楚这种动力学限制在大气中有多大的问题。[然而,使用的一些参数化确实考虑了动力学限制(例如,c.c.c uang等,1997)。]
此外,这些传统的Köhler曲线没有考虑到微可溶性溶质或可溶解在颗粒中的气体的影响。图14.38b比较了(NH4)2S04在298 K的30 nm干颗粒与含有500 nm微溶CaS04核心的相同颗粒的传统Köhler曲线(Kulmala et al., 1997)。粒径的增加降低了开尔文效应的贡献,曲线中的最小值反映了所有CaS04溶解的点。还显示了存在1ppb气态HN03并被颗粒吸收的情况下的Köhler曲线。可以看出,在~ f 0 /¿m范围内,平衡过饱和小于1;即,对于这种更复杂(但现实)的情况,云滴可以在RH低于100%时形成。
小颗粒生长到Köhler曲线右侧的足够大小的可能机制包括小颗粒被吸收到现有的云滴中,在云内发生气体物种(如S02)氧化成硫酸盐。云的蒸发会留下一个更大的颗粒,其中含有额外的氧化产物(例如,见Hoppel和Frick, 1990;赫格,1990;Van Dingenen等人,1995;和Hoppel等人,1996)。颗粒生长的其他可能机制包括细颗粒的凝固或现有颗粒通过低挥发性产物的凝结而生长(例如,见Lin et al., 1992,1993a, 1993b;赫格,1990,1993)。然而,混凝在偏远地区并不重要,因为颗粒的数量浓度远小于混凝可能很重要的污染地区(Lin et al., 1992)。
正如我们已经看到的,与Köhler曲线的峰值相对应的临界过饱和Sc.取决于气溶胶粒子特有的若干参数。因此,在一定的过饱和状态下,有些粒子会形成云滴,有些则不会。因此,CCN的总数将随着CCN测量中使用的过饱和而变化。图14.39说明了这一点,其中显示了在南极洲测量到的CCN浓度是CCN过饱和百分比的函数,这些CCN分别生长成大于0.3和0.5 /¿m的液滴(Saxena, 1996)。这组特殊的测量
继续阅读:氮氧化物水平
这篇文章有用吗?