测定气相反应绝对速率常数的实验室技术
在本节中,我们将讨论用于确定与大气化学有关的气相反应的绝对速率常数的主要实验方法。这些包括快流系统(FFS)、闪光光解(FP)、静态反应系统和脉冲辐射解。相对速率常数的测定将在C节讨论。
一般来说,我们使用这种类型的简单双分子反应
作为插图。然而,如前所述,这些技术可以被修改以研究三分子反应,以及单分子反应。
为了研究相对活性物质a与反应物B的反应动力学,人们通常会在B大量过量的情况下损失少量的a。这就要求人们首先能够生成a,然后监测其浓度随时间的变化。理想情况下,为了充分阐明反应机理,还可以监测中间体和产物的浓度。正如我们将看到的,在实践中,对于许多反应来说,这比简单地确定速率常数本身要困难得多。
1.动力学分析
简单双分子反应如(17)的速率定律由
如果在大量过量的B中产生少量的a,那么即使(f7)被允许完成,B的浓度将基本保持在初始浓度[B]()不变。对(S)积分,将[B]0作为常数,可得
也就是说,A随时间呈指数衰减(k 17 [B]”),就好像它是一个一阶反应。因此,在这些所谓的伪一阶条件下,对于给定的[B]()值,ln[a]随时间的曲线应该是线性的,斜率等于(- &I7[B]0)。这些图是对[B]0的一系列浓度和确定的相应衰变值进行绘制的。最后,绝对利率常数kxl是这些衰减率绝对值与[B]0对应值的曲线斜率。下面将讨论一些示例。
正如我们前面所看到的,即使是三阶反应,只要保持除A以外的所有物质的浓度不变,并且A的浓度远远超过A,就可以简化为伪一阶反应。这种使用伪一阶条件的技术是迄今为止最常用的确定速率常数的技术。它不仅只需要监测一种物种A作为时间的函数,而且甚至不需要测量A的绝对浓度。由于比例[A]/[A]0出现在Eq. (T)中,测量任何与A浓度成比例的参数都足以确定kl7,因为该参数与[A]之间的比例常数在Eq. (T)中抵消。例如,如果A在一个方便的光谱区域吸收光,并且遵循比尔定律,那么给定浓度A的吸光度(Abs) N(数字cm-3)由
式中/ "和I分别为入射光强和透射光强,/为光程长度,a为吸收截面(以e为底)
将[A] = N = Abs / A I代入Eq. (T),可得
(Abs/o7) (Abs) In = In = -kl7[B]0t, (V)
其中(Abs)和(Abs)0分别是A在t和t = 0时刻对光的吸收。例如,03在254 nm处有很强的吸收,可以用来监测它的浓度。
这种监测与浓度成比例的参数的能力,而不是绝对浓度本身,在大多数动力学研究中提供了一个实质性的实验优势,因为确定原子和自由基的绝对浓度通常是困难的。
这种伪一阶动力学分析通常应用于无论所使用的实验系统。
2.Fast-Flow系统
快流系统(FFS)由一个直径通常为2- 5cm的流管组成,其中反应物a和B在大量惰性“浴气”(如He或Ar)的存在下混合。当混合物以相对较高的线性流动速度(通常为1000 cm s~’)沿着流管流动时,a和B发生反应。A沿流管长度的衰减,即随时间的衰减,然后应用Eq. (T)得到感兴趣的速率常数。
快速流动这个术语来自于高流动速度。在大多数这样的系统中,放电被用来产生A或另一种A的前体;因此,术语快流排放系统(FFDS)也通常被应用。由于快流放电系统已应用于许多与对流层化学有关的动力学和力学研究(例如,见Howard, 1979;考夫曼,1984),我们集中研究它们。然而,所有的快流系统都依赖于相同的实验和理论原理。
图5.4为原理图一个典型的快流排放系统。活性组分在微波放电中产生,并从上游进入
-
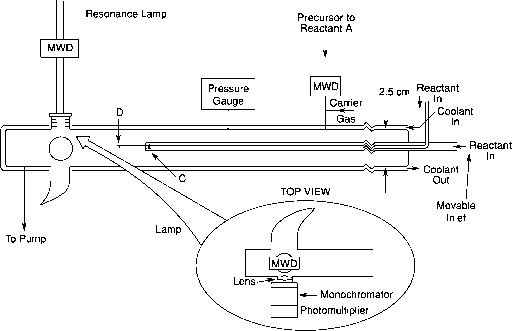
- 图5.4快流排放系统示意图(改编自Beichert et at。, 1995)。MWD =微波放电,用于从前驱体产生反应物种,并产生适当波长的光,以使用谐振灯测量它。
第二反应物通过可移动进气道的C或D端口加入。检测器固定在流动管的下游端,通过移动C和D的混合点(即可移动的入口)相对于固定检测器来改变反应时间。
例如,OH可以由H与NO反应生成:
原子氢是通过释放稀释的H2/He混合物而形成的。然后这些H原子通过加入过量的N02转化为OH,例如通过c端口。通过适当调整N02的浓度,基本上所有的H都可以在第二个反应物通过D端口加入之前转化为OH。
表5.3显示了FFDS中使用的一些典型的大气活性物质来源,而表5.4显示了用于检测它们的一些方法。
在塞流假设成立的情况下,即浓度梯度可以忽略,使得载气的线性流速与反应物的线性流速相同,A和B沿流管行进距离d的时间(t)为d t = -。
其中v为线性流速,可由流动管截面积(ar)、流动管内总压力(p)、温度(T)、反应物和稀释气体的摩尔流速idn / dt计算得出:
继续阅读:离子强度与速率常数
这篇文章有用吗?
