吸收截面

根据液体和固体各自分子的吸收特性来确定它们的吸收系数并不是一件容易的事情，因为它们靠得很近，相互作用很强。从图1.11和1.12可以明显看出，液态水的光谱发射率与水蒸气的光谱发射率几乎没有相似之处。从后者开始，向前者迈进并非易事。在液相中，水分子之间的相互作用几乎破坏了它们的个性。然而，对于气体和粒子悬浮液，我们确实有希望从单个分子或粒子的性质开始确定吸收系数。

所谓粒子，我们指的是数量足够多的分子的集合，它具有宏观性质，如温度和压力。分子的温度和压强是不存在的。甚至分子的半径也是一个模糊的数字:每种测量分子直径的方法都会得出不同的结果。粒子本身可能由具有吸收系数的物质组成，但不存在单个分子的吸收系数这样的东西。同一种物质的所有分子本质上都是相同的，但是每个粒子都不同于其他粒子。像温度和压力一样，吸收系数是一个统计量，是许多分子集合的平均值。

我们认为气体的吸收系数取决于其分子的浓度。毕竟，吸收系数的倒数是吸收长度，如果同一浓度的气体与更高浓度的相同气体具有相同的吸收长度，这几乎没有意义。这里用浓度而不是密度来强调对的吸收电磁辐射根本不依赖于质量。电磁波把力施加在电荷上，而不是质量上，它们只是随大流。当你使用非限定术语密度时，请确保你清楚你指的是质量密度(单位体积的质量)还是数量密度(单位体积的分子数)。我们用数字密度和浓度来表示或多或少相同的东西。

假设一个孤立的分子被单向的单色光束F照射。这个分子吸收能量，也就是说它以与F成正比的速率Wa将辐射能转换成其他形式。Wa的维度是功率，而F的维度是单位面积的功率。因此，两者之间的比例因子aa必须具有长度平方(面积)的维度。因此aa被命名为吸收截面。这是分子从入射光束中去除能量的有效面积，不应该与分子的几何横截面积相混淆，即使这样的面积有精确的含义，但它并没有。栖息在大气中的各种分子的直径约为3 × 10~8厘米，对应的几何截面积约为7 × 10~16厘米2。但是分子的吸收截面通常比这个值小得多。

如果被照亮的物体是粒子而不是分子，式(2.28)同样成立。关于粒子的吸收截面，我们将在2.9节中详细说明。

各种截面在物理学的几个领域都是基本的，如气体动力学理论、中子物理学、高能粒子物理学和光学。

假设一个面积为a，厚度为Ax的薄板气体，每单位体积有N个分子，吸收截面为aa，被垂直于薄板表面的单向单色光束照射(图2.6)。平板中分子的总数是NAAx，因此从光束中去除辐射能的总有效面积是aaNAAx，我们假设在光束的方向上没有分子重叠(或阴影)另一个分子。传输功率在距离Ax上的减小值为

其中F是入射辐照度。由此可知，AF = -FNaaAx = -FkAx，

其中k = Na为式(2.1)中的吸收系数。

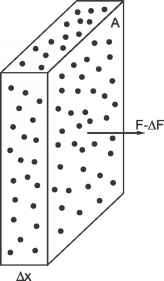
图2.6:入射在吸收分子随机分布的平板上的辐照度F衰减量与平板中所有分子的总横截面积(投影有效面积)成正比。

我们含蓄地假设所有的分子都是相同的。然而，即使它们是，它们也不可能全部朝向相同，因此式(2.31)中的吸收截面应被解释为平均值。因为k是可加性的

式中j表示特定分子取向，式(2.31)中的va是取向平均值

如果所有方向都是等可能的(随机方向)，所有横截面的权重都是相等的。

方程式的另一个假设。(2.31) -(2.33)是干涉(相干)的后果可以忽略不计(见第3.4和5.1节)。如果不是这样，要确定在任何x处透射的辐照度，我们就不能跳过确定电场和磁场的振幅和相位这中间步骤，从而得出辐照度。

如果分子不对称，吸收横截面也取决于光束的偏振状态(见第7章)。但如果分子的方向是随机的，气体的吸收系数与极化无关。

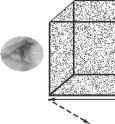
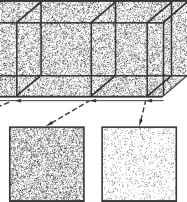
图2.7:方形管中随机填充了25000个粒子(黑色方块)。观察者会看到什么(向右看)在不同的点沿着这条管被描绘在下面的正方形。

我们所说的关于气体吸收的一切，同样适用于粒子的悬浮。所要做的就是用粒子的吸收截面代替分子的吸收截面(见第2.9节)。

方程(2.7)表示指数衰减，气体(或悬浮粒子)的吸收系数由方程(2.31)给出，其中包含了值得公开的隐藏假设。即使相干性可以忽略不计，一个分子或粒子影响其他分子或粒子吸收的可能性仍然存在。假设，例如，一个管包含固定数量的吸收器，每个吸收横截面相同。它们在空间中的分布决定了它们的衰减。如果所有的吸收器恰好一个接一个地排列，那么它们的总投影吸收面积就是单个吸收器的吸收截面。但是如果它们的分布使得没有吸收器在另一个吸收器后面，它们的总投影吸收面积就大得多。即使管中吸收器的总数相同，这两种空间分布的衰减也有很大不同。所有的吸收器排成一排在物理上是不现实的(晶体除外)，但这种极端的分布表明，吸收器的投影吸收面积重叠的方式决定了它们的衰减。

为了进一步探讨，我们计算了用黑色方块表示的两种可能的吸收剂排列，以后称为粒子。一个面积为4个单位的大正方形，代表一个方形管的横截面积，按照两种不同的配方填充横截面积为0.0001单位的相同颗粒。在某一处方中，随机选取大方格内颗粒的位置，依次添加到大方格中，记录总累积颗粒面积(图2.7)。从累积粒子面积中减去一个新增粒子与管中所有其他粒子重叠的总面积，就得到了总投影面积。在另一种处方中，粒子不允许重叠。如果一个粒子的位置与其他粒子重叠，它就会被重新定位以消除所有重叠，因此产生的粒子分布并不是完全随机的。

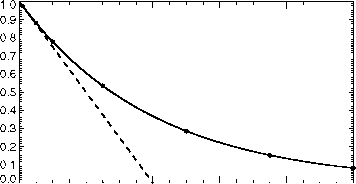
20000 40000 60000 80000管内颗粒数量

100000

20000 40000 60000 80000管内颗粒数量

100000

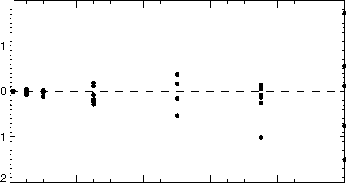
图2.8:上图显示了两种不同处方的透射率与粒子数量的关系:重叠粒子(实心圆圈)和非重叠粒子(虚线曲线)。固体曲线上的每个实心圆(指数衰减)都是对1000、5000、10,000、25,000、50,000、75,000和100,000个粒子进行六组计算的结果。由于在图的上半部分无法解决六个集合的变化，下半部分显示了每个计算的透过率与指数下降透过率之间的差值相对于指数下降透过率的比值。

1减去粒子的总投影面积除以管的横截面积即为透射率，图2.8显示了重叠和非重叠粒子的透射率。对于足够小的粒子数量，透射率是相同的，但随着这个数量的增加，两条曲线发散。对于重叠粒子，透射率

波长(| im)

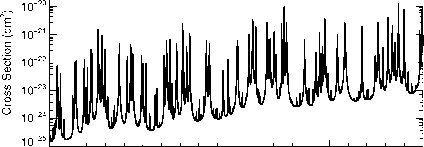
图2.9:温度为20℃，总压为1个大气压时，水分子的吸收截面。

波长(| im)

图2.9:温度为20℃，总压为1个大气压时，水分子的吸收截面。

密切遵循指数定律exp(-NAp)，其中N是管内粒子的总数，Ap是粒子相对于管内横截面积的横截面积。图2.8实体曲线[exp(-NAp)]上的每个点都是六组计算的结果，每组计算的结果都略有不同，尽管它们都是不可解析的。为了解决差异，图的下半部分显示了每个计算的相对偏差，定义为计算的透射率与指数定律预测的透射率之间的差值相对于指数定律的差值之比。

对于不重叠的粒子，透射率随粒子数的增加呈直线1 - NAp下降，衰减速度大于指数衰减。如果所有的粒子都在一条线上，那么对于所有的n> 0，透射率将是1 - Ap。由此我们得出，式(2.7)适用于吸收剂的完全随机分布。如果吸收剂的位置是相关的，指数定律就会受到质疑，尽管我们还没有实验证据表明这种情况在大气分子或粒子中发生过相当大的程度。

现在我们能够更好地理解均匀湿润空气层的光谱发射率曲线的起源(图1.11)。我们用Eq.(2.24)得到了这条曲线，k由Eq.(2.31)给出。因此发射率的频率依赖关系源于水分子吸收截面的频率依赖关系(图2.9)。我们可以把厚度为h的均匀湿空气层的法向发射率写成mw

pw在哪液态水密度， mw是一个水分子的质量，d是一个液态水层的深度，如果潮湿空气中的所有水蒸气分子都是

与

凝结成液体。量Nhaa是吸收光学深度ra(见第5.2节)，当d =1 cm时为3.3 x 1022 aa，横截面为cm2。

的吸水截面蒸汽(图2.9)在所示红外频率范围内变化超过1000倍。在峰值处，截面足够大，对应的发射率几乎为1，在波谷处，远小于1(图1.11)。吸收截面并不是严格意义上的分子性质，而是取决于与相邻分子的相互作用，即使在气相中也是如此。峰的位置没有它们宽度的变化那么大，这并不特别难解释(就像我们随后所做的那样)。图2.9所示为吸收系数除以N, N定义了有效吸收截面，即分子和环境的性质，我们计算的总压力为1atm，温度为20°C。要解释横截面的频率依赖性，我们必须深入挖掘。要做到这一点，我们需要正确的方法，即复杂变量的基础知识，我们接下来将讨论这一点。

继续阅读:吸收的经典与量子力学解释

这篇文章有用吗?

+ 2 －1