复杂的折射率
理论的散射和吸收均匀粒子包含一个材料参数,它复杂的折射率。最简单的方法来证明折射率可以写成复数是考虑一个平面,标量波传播方向+ x光的均匀介质:
相速度v波的w / k。如果光速c是空间我们可以重写这个
v是介质的折射率的波传播。但这波不能物理现实的因为它不是减毒如果是恒定的。让我们允许波衰减指数通过编写其振幅exp(用户体验/ c - n”)。(3.118)
现在,波的形式
复杂的折射率在哪里吗
我们改变了符号的实数部分从n, n’。或者,我们可以说,情商的波数。(3.115)是复杂的,把它写成k = n = k +本土知识”。(3.121)
现在我们应该适应复杂的波数,因为我们知道,解决线性方程,如我们已经考虑的波方程,可以表示为复杂的功能(见2.5秒。)。因为时间上权力由介质中的波传播与一个复杂的折射率(一个因素除外)
= = a2 exp {2 n 'W / c} = a2 exp {4 nn”/}, (3.122)
在= 2数控/ u是自由空间波长,我们立即获得折射率的虚部之间的关系和k的吸收系数表示第2.1节,然后在2.8节改为Kb区分批量(均匀)媒体和悬浮液的颗粒:
符号也用于体积吸收系数在Eq。(3.123)。
符号和公约对于复杂折射率有时造成混淆,可以导致严重的错误。为我们各频率惯例,n和n”都是负的。但是你经常遇到复杂的折射率写成
再次,n和n”都非负。这是正确的,情商Eq。(3.120)或(3.124)?都在使用适当的公约。如果公约exp (wt), Eq。(3.120)
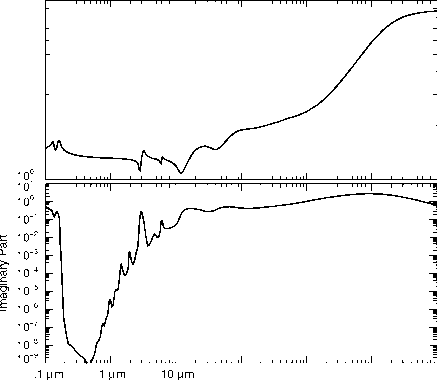
1毫米波长。
1毫米
图3.8:光学常数(复杂的折射率)的液态水从编译Querry et al。(1991)引用了第二章的末尾。
1毫米波长。
1毫米
图3.8:光学常数(复杂的折射率)的液态水从编译Querry et al。(1991)引用了第二章的末尾。
对应的波,振幅降低的方向传播;如果公约exp(艾维),Eq。(3.124)对应于这样的波浪。如果我们能设计出波振幅增加传播的方向,没有外部供给能源,能源危机将立即蒸发。约定既没有对也没有错。有什么问题是混合约定,确定导致事故(如在路的右边开车在英国)。
复折射率通常是写N = N +逆向运动,与N和k称为光学常数(特别是通过测量它们的人)。但正如掌玺大臣既不是神,也不是私人的,也不是海豹,光学常数既不是光学(只属于可见或near-visible频率)和常数。事实上,他们明显不同的频率从无线电到紫外线(图3.8)。此外,它们并不是独立的,可调参数,分别可以取任何值。实部和虚部联系。如果一个变化,所以必须。例如,大约下午3点,一个大的变化在水的折射率的虚部(吸收带)是伴随着一种变体的实部(图3.8)。
真正的折射率和相速度
一些概念被糟糕的教科书,充塞着更多的神话和显而易见的无稽之谈,折射率,复杂的或以其他方式。例如,它已经无数次声明,折射率(这是真正的部分)是更大的在一个密集的媒介。是的,它是真实的空气折射率小于一千倍的密集的水最多,也许所有的(我们不知道),频率。但就其本身而言。很幽默但熏陶注意折射率和(质量)密度是半个世纪前发表的r·斯科特·巴尔末在美国物理学杂志》上(这应该是阅读和物理教师的绝对必须读物理教科书的作者)。图1的标题巴尔的读取”直接与密度折射率变化吗?”This figure shows refractive index versus density (at a given frequency in the visible) for a few dozen substances. The points are connected to answer the question in the caption: NO. Barr confesses that these points "were not selected entirely impartially", so shows another figure in which refractive index versus density is plotted (for a given temperature and wavelength) for 445 organic materials. As Barr notes, "this figure indicates that if a material has a high density it is more likely to have a high index than a low one, but that is about all that can be said." Actually, the picture is much bleaker than Barr paints. It is no trick at all to find two materials with different densities for which at one frequency the refractive index is greatest for the denser material but at another frequency is least. And now the clincher: there are plenty of dense, solid materials with lower refractive indices at some frequencies than that of such diaphanous substances as air. And these materials are not exotic or "anomalous", but close to hand. For example, at a wavenumber of about 530 cm-1, the real part of the complex refractive index of magnesium oxide (made by burning magnesium wire in air) is 0.093. If magnesium oxide is too exotic for your tastes, try glass (silicon dioxide), with a real refractive index of 0.39 at 1250 cm-1. And then there is ordinary table salt (sodium chloride), with a real refractive index of 0.14 at 200 cm-1. Examples abound. We did not have to search high and low for them.
但是有提到折射率接近于零的水平,我们预计的不满从那些被教导说,没有什么能超过光速。这确实是真的,根据狭义相对论没有东西能超过光速,但是固定相表面不是一个东西。这是一个虚构的表面移动的相速度v .狭义相对论也规定信号不能传播速度比c,但一个平面,情商等谐波。(3.33)不能发送一个信号。你可能有一个调幅-调频收音机。我代表调幅、调频频率调制。广播电台,尽管宣布一个广播频率,绝不传输单色波。项目通过这样的海浪将是极其沉闷:持续的嗡嗡声。传输一个信号(信息)需要调制波。考虑到摩尔斯电码的简单例子。一个稳定的信号传达任何信息。 To convey information by Morse code requires turning something on for a brief instant, then off, varying the time intervals between off and on and the length of the time on. That is, the steady tone must be modulated. And so must speech in order to be understood. Try carrying on a conversation at a party by steadily grunting at a single frequency. You won't be invited again. Because the phase speed is neither the speed of a thing nor the speed with which signals are propagated, it is not constrained to be less than c, and hence the real part of the refractive index is not constrained to be greater than 1.
学生偶然发现实际折射率小于1可能安抚被告知群速度不能大于c。唉,调用群速度只会让事情变得更糟。要理解为什么,我们首先需要解释的群速度。考虑两个波的振幅,一起宣传,频率与波数k±Ak / 2 w±Aw / 2,在一个中等我们采取nonabsorbing (N = N, k是真实的),方便。后这两个波的总和(代数,看到Eq。(3.63)]
^ 2 = exp {ikx - iwt}因为{Akx / 2 - Awt / 2}。(3.125)
这个描述平面谐波与相速度w / k是一波又一波的振幅和波长更大(小得多的波数)和相应的频率要小得多。这样的速度长波长包络调制的更短的波长波是啊/ Ak,群速度的定义(速度,真的)vg的极限
1 Ak dk
FromEqs。(3.117)和(3.121)我们有wn 1 k n k = -, - = - = -。(3.127)
介质中n取决于w叫做色散,而是因为一个真正的非色散介质不存在(除了可能空白空间),这一项不是很独特。但分散一词表达一组波的传播在媒介不会粘在一起。驱散的意思是“成为相隔。”
如果dn / dw = 0, vg = v = c / n,和一群一波又一波的不同频率和wavenum-ber都有相同的相位速度,因此不会分散。我们可以重写Eq。(3.128)
正常色散一词应用dn / dw > 0时,反常色散当dn / dw < 0,但没什么“反常”的反常色散。所有材料表现出反常色散在某些频率,当一切都是异常的,没有什么异常。在正常色散的频率区域,vg < v;在反常色散区域,vg >诉当我们仔细检查Eq。(3.128)我们到达一个惊人的结论。假设dn n +铜- < 0,(3.130)
dw只能满足在反常色散区,dn n + w dw
如果这两个条件都满足了群速度为负,其重要性大于c:光打破了速度限制旅行时走错了路。这就是为什么我们说,调用群速度当面对阶段速度大于c只会让事情变得更糟。有任何真正的材料满足方程式。(3.130)和(3.131)?吨的他们,在你的早餐桌上:群速度在食盐200 cm - 1的频率大约是4 c。
违反的限速c是一个粗心大意的结果,如果不是彻头彻尾的草率,方法使用术语光速。(至少)有四个不同的光的速度:相速度、群速度,信号的速度和能量传播的速度。所有四个不同色散媒质,但只有其中一个不能大于c。顾名思义,信号传播速度的速度信号。假设一个源色散媒质中突然打开。在时间t探测器距离d从源开始注册一个信号。狭义相对论说,d / t比值不能大于c。摩尔斯电码,只能通过将通过光信号来源。
虚粒子折射率和吸收
虽然复杂的折射率的实部是被误解,当我们转向虚部我们遇到那么多废话,旋转。如果你认为我们夸大,考虑下面的故事,我们没有(或可能)。几年前我们遇到复杂的折射率测量推断,乍一看似乎不容置疑的。可见(激光)的散射光与散射角单悬浮球体被一个非线性最小二乘分析产生适合他们复杂的折射率。什么会更完美呢?一个粒子,已知球面均匀,理论无疑是适用的。在报纸上报道的假想(不止一个意义上)折射率因此获得的材料之一是石油的指数是0.01。这种油的瓶子至少10厘米直径。从情商。(3.123),对应的可见波长的吸收这种油的长度大约是下午5点。因此我们必须得出石油涌出一个瓶子直径约20000吸收长度。 To show that 0.01 is wrong by at least a factor of 10,000 all you have to do is pick up a bottle of the oil and note that you can see through it. What went wrong? In the first place, the experimenter did not know, did not understand, or was incapable of drawing any conclusions from Eq. (3.123), the fundamental equation relating n'' to a more directly measurable and understandable quantity. He also violated the first commandment of measurements: Thou shalt know the magnitude of what you intend to measure before you measure it. Without knowing this magnitude you cannot design a proper method for reliably measuring it. The method under scrutiny here lacked sensitivity. Within experimental uncertainty, the angular scattering pattern was the same for imaginary indices of 0.000001 and 0.1 and everything between. So the inferred, but hopelessly incor rect, imaginary index 0.01 was the experimental error for a correct value at least 10,000 times smaller.
误解虚指数是大气科学文献的规则。他们通常被视为可调参数,没有理解他们的大小或他们如何随频率不同的材料。通常发现一个虚构的断言指数0.01对应的“软弱”吸收(可见波长),大概是因为0.01度1。但是正如我们所见,一个虚构的指数0.01对应于一个吸收长度为几微米。
一个气溶胶是悬浮颗粒的气体,包括气体。已经耗费了大量的无意义的努力决定大气气溶胶折射率的即使它不存在,就像一头牛的折射率或亚马逊丛林并不存在。我们这里是无法区分的属性的物质和身体。的折射率是一个属性(均匀)材料,不非均质体。没有复杂的折射率等实体的大气气溶胶,不断变化的女巫的酿造含粒子的不同和一般未知成分,大小和形状。单个粒子甚至可能不是由单一材料但骨料颗粒,像葡萄干面包涂上芝麻。
的复杂的折射率均匀(波长的规模)材料或多或少是一种定义良好的数量,原则上可以衡量的,尽管在实践中这可能是困难的。让我们后退一步,大纲如何测量折射率实验谁知道他们在做什么。折射率不能直接测量,但推断,通常由均匀样品测量的反射和传输(板)感兴趣的材料。这些样品光学平滑,均匀,厚度。反射理论和传输等板折射率的函数用于转化测量来获得所需的折射率。听起来很简单。但是有几个问题。一是理论适用于样本。因此,如果理论是对的镜面反射均匀,均匀样本,样本更符合这个血腥的好。此外,测量量时必须改变折射率的变化。如果折射率只繁殖测量用于获得它,那将是没有价值的。也就是说,如果我们能做的就是推断折射率测量的反射率和透射率,然后用它来计算这些相同的量(在实验误差),我们只是追逐尾巴。但正确测量的光学常数有更广泛的有效性。例如,他们可以用来计算反射和传输任何厚度的板,或由均匀粒子散射和吸收任何大小和形状(理论的存在)。这不是尾追逐。
现在考虑粒子在大气中。一般来说,它们的大小、形状和成分都不知道。他们可能不均匀,浓度(数密度)点对点不同,的时候。与样品准备在实验室,实验无法控制大气粒子的特性。然而,一个可以让各种测量的散射。出现问题时,然而,当一个人试图转化这些测量获得的(不存在的)折射率粒子,一个复数在给定波长,在某种意义上是一个有效的光学性质。测量和所需的数量从它总是出来的理论。什么理论用于转化测量大气粒子的散射?米氏理论(请参见下一部分),当然,这是有效的只有均匀球体,可能结合成平行面的辐射传输理论,统一的媒介。反演方案基于这个理论将尽职尽责地给结果,尽管在油滴的例子,他们可能是完全错误的。 All that one can say for sure is that the inferred quantity is consistent, within experimental error, with the theory: if you invert the measurements with Mie theory to obtain refractive indices, then use these refractive indices in Mie theory, you will recover (within error bars) the measurements. All you are doing here is chasing your tail.
现在对比人一直试图为大气中的粒子与前面所讨论的测量油滴。实验者有绝对控制他的样本:一个单一的、均匀球体,已知的大小和构成。然而,错误在他虚指数从测量推断至少10000倍。想到多少难测量(远程)粒子的折射率,大小分布、形状、成分和浓度的未知和实验者没有控制。
全面,气象学家不太了解电磁理论,光学和固体物理学。但他们知道很多关于流体力学(或者至少是它的一个分支)。如果我们提出的“有效”粘度测量大气系统,气象学家在笑翻一番。甚至最天真的modeler试图模型的动态耦合海洋和大气把这个系统作为一个单独的和某种虚假的有效粘度的液体吗?我们认为不是。但这些人毫不犹豫地吞下同样虚假的大气气溶胶的有效折射率的概念。
继续阅读:散射的各向同性均匀球体
这篇文章有用吗?