散射相移
考虑两个相同的偶极子(图3.5)被单色(标量)平面波照射,或被一个横向相干长度远大于它们之间间隔的源照射,波数k = 2n/X。假设它们主要由入射波激发,相互激励可以忽略不计。由于两个偶极子被同一入射波激发,被它们散射的波具有固定的相位差,这取决于它们之间的距离、照明的波长和观测的方向。用e表示;入射波的方向,由es1和es2的方向散射波(指向观测点O的方向),以及偶极子2相对于偶极子1的位置r12。虽然散射波或多或少是球形波,但我们认为观测点足够远,可以认为它们是局部平面波。即使光是矢量波,我们也考虑标量波,因为我们只对相位差感兴趣。如果入射波在1处的复振幅为a,在2处的复振幅为exp(ike;•r12)。因为每个散射波的振幅与
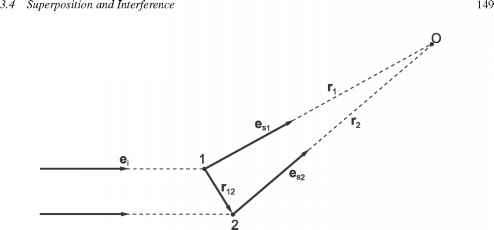
图3.5:在O点,总散射场是两个间隔固定距离r12的偶极子散射场的叠加。这两个场之间的相位差取决于入射方向和散射方向之间的角度以及相对于照明波长的偶极子之间的距离。
图3.5:在O点,总散射场是两个间隔固定距离r12的偶极子散射场的叠加。这两个场之间的相位差取决于入射方向和散射方向之间的角度以及相对于照明波长的偶极子之间的距离。
激发它的波的振幅,在O处的两个散射波是
= aexp(ikesi■ri), = aexp(ikesi■r12 + ikes2■ri - ikes2■r12), (3.92)
两个波的任何共同因子都被省略了。随着到观测点O的距离无限增加,es2 ^ es1 = es,两个波之间的相位差逐渐接近
A(p = k(ei - es)•ri2 = ^-(e;- es)•ri2。(3.94)
从这个简单的方程式中,我们对物理有了惊人的理解。
向前的方向是入射波的方向。根据式(3.94),无论两个偶极子的分离和波长如何,正向(es = e;)散射始终处于相位(A^> = 0)。这是唯一的散射方向,它是正确的,因此向前的方向是奇异的,一个我们返回的点。
任何粒子都是N个偶极子的相干阵列。同样,我们假设它们主要是由入射波激发的。如果该阵列的线性范围与波长相比较小,则所有分离的散射波在所有方向上都近似相位差[见式(3.42),其中A^> = 0和a1 = a2],因此N个散射体在任何方向上散射的功率是散射1的功率的N2倍。如果粒子的总体积为v,每单位体积有n个偶极子,则偶极子的总数与v成正比。因此,我们预测,与波长相比小的粒子散射的总功率与v2成正比。正如我们在第3.5节中所展示的,这是正确的。
偶极子之间的相互作用是不可忽略的,除非相隔足够大的距离。虽然这个条件还不能满足一个小散射粒子,即使考虑到相互作用,其体积的平方仍然会增加(相互作用意味着每个偶极子发出的波会明显地激发相邻的偶极子)。原因是,如果粒子足够小,即使相互作用也不可能有明显的相位差。因此,偶极子(粒子)的阵列是近似相干和同相的,即使偶极子相互激发。
让我们继续这样做,看看基于式(3.94)的物理推理能得到什么一般结果。随着粒子整体尺寸的增加,由其组成偶极子散射的波之间的相位差也增加。当粒子足够小时,所有这些波在所有散射方向上都近似相位差(建设性干涉)。但随着颗粒尺寸的增大,某些方向可能出现n阶或更大的相位差。特别是,两个或多个偶极波之间的相位差可以使它们在特定方向上发生破坏性干涉。因此,我们得出这样的结论:当粒子与波长相比较小时,尽管粒子散射以其体积的平方增加,但这种快速增加不可能无限期地持续下去。随着颗粒大小的增大,散射也随之增加,但速度比体积的平方要慢。同样,这一预期也得到了详细计算的支持(参见第3.5.1节)。我们可以通过简单的相位差参数,至少在定性上理解它们。
我们在第3.2节中表明,偶极子散射(受限制)与入射照明波长的四次方近似成反比。但这并不一定意味着这种偶极子(粒子)相干阵列的散射也遵循这种波长依赖关系。如式(3.94)所示,一个额外的波长依赖通过相位差悄然进入。事实上,对于足够大的粒子,单个偶极子散射的波长依赖性的净效应几乎抵消了由相位差引起的波长依赖性。在下一节中,我们将给出一个简单的例子来详细说明这一点。
现在让我们转向散射的方向依赖关系。假设我们的两个偶极子在各个方向上都有相同的散射。这并不意味着两者的散射在所有方向上都是一样的。根据式(3.94),两个散射波之间的相位差取决于散射方向。我们可以通过考虑与入射波平行的一条线上的两个偶极子(ri2 = re;)的特殊例子来使这一点更清楚相移(再次强调,交互作用被忽略了)
其中d为散射角(入射波与散射波的夹角)。两个偶极子在任意方向上的散射功率由cos Ay决定。量1 - cos d在0(正向)和2(反向)之间,因此相位差在0(正向)和4nr/A(反向)之间。当(向后)相位差是n的奇数倍时,干扰是破坏性的;当相位差是n的偶数倍时,干涉是建设性的;当然,这两个极端之间的一切都是可能的。随着r/A的增加,散射图中的振荡次数也增加(散射是角度的函数)。
粒子越大,其各元素之间的平均距离也越大。因此,我们期望,在两个偶极子的行为的基础上,一个粒子的散射图显示更多的极大值(最小值)相对于波长的大小越大。这一预期由详细的计算(第3.5.1节)和测量所证实。
因为散射是无论波长和偶极子之间的分离如何,我们期望在这个方向上的散射比在任何其他方向上的散射随尺寸的增加更快。同样,这一预期是由计算(第3.5.1节)和测量所证实的。一般的结果是,粒子越大,被它散射的正向峰值越大。
相位差相对于r的变化率从正向的0到逆向的4n/A。这意味着,如果我们有固定数量的偶极子(固定的粒子体积),我们移动它们(改变粒子形状),散射在前进方向上受到的影响最小,而在向后方向上受到的影响最大。同样,这也得到了计算和测量的支持。
大部分粒子散射的基本物理都体现在式(3.94)中给出的简单相位差中。其余的是细节,其中一些我们在第3.5节中给出,但首先我们讨论空气和水的散射。
继续阅读:复折射率
这篇文章有用吗?