由偶极极化散射天窗
在前一节中,我们考虑镜面反射通过无限接口,定义的入射面是正常的界面和方向(入射波的波矢)。但是我们可以定义这个平面的方向和入射光的反射或折射波。实际上,这就是在有限的对象:散射的问题定义的散射平面的方向入射波和散射波的能流密度矢量。在章节3.4和3.5,我们讨论的频率和角度而不是散射的偏振依赖性。我们将这宽松的结束。
考虑一个球对称电偶极子被一架飞机谐波。我们把周围的介质可忽视地吸收。我们可能考虑的可能性微乎其微的偶极子是一个球体尺寸相对波长。入射波激发的偶极子辐射(即。,向四面八方散射)。的方向入射波和散射波的能流密度矢量不平行于入射波定义一个独特的散射平面,和我们将自己限制于散射方向躺在这个平面上。和入射光的电场散射波躺在不同平面垂直于散射平面(图7.8)。表示和E |;入射波的两个组件,垂直,平行,分别散射平面;E±s和E | s散射场的组件。因为假定球面对称的偶极子,入射光偏振垂直于散射平面只能产生散射场垂直于这个平面。这同样适用于入射光偏振散射平面平行。因为线性方程的电磁场这些分散的字段组件,像镜面反射组件,事件字段组件成正比,激发他们:
E±s«E±i, E | |年代«E | |;。(7.110)
当入射场垂直于散射平面由偶极子场分散不能依赖于散射角在这个平面上。你可以把握这个通过观察针垂直于一张纸。当你改变你的浏览方向在这个表中,针看起来总是相同的。但两个或两个以上的平行针隔开的距离与波长相比较小不同会不同
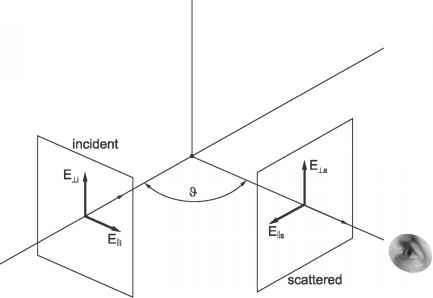
图7.8:两个方向的入射和散射波,确定一个平面,平面散射。垂直入射和散射领域可以解决到组件(±)和并行(| |)这架飞机。入射电场是固定的基向量与散射角散射场变化而英国《金融时报》。
图7.8:两个方向的入射和散射波,确定一个平面,平面散射。垂直入射和散射领域可以解决到组件(±)和并行(| |)这架飞机。入射电场是固定的基向量与散射角散射场变化而英国《金融时报》。
方向(参见秒。3.4)。这种独立性的字段在一个偶极子方向垂直于入射场时散射平面是完全通用的,但是,当入射场散射平面平行,我们必须实施一个附加条件。想象一个球面极坐标系统(r, tf, y)以偶极子。在任何时候,散射场的径向分量(r-component)以及切向分量。但径向分量减少更快随着r比切向分量。在足够大的距离相对波长,所谓的远场的径向分量就可以忽略不计。我们可以做一个简单的,但不严谨、论证的角散射远场时的依赖入射辐射散射平面平行。图7.9描述了偶极子场Ed,兴奋的事件并行领域,产生散射场组件平行(径向)功能和散射方向垂直(切线)美国东部时间。但在远场的径向分量可以忽略不计,只留下切向分量,与Ed cos成正比的tf, tf是散射角。通过这种原油参数我们得出结论,在远场
我们必须提到一个额外的字段组件的依赖,尽管它没有极化的至关重要的作用在我们的讨论。想象一个任意半径的球体
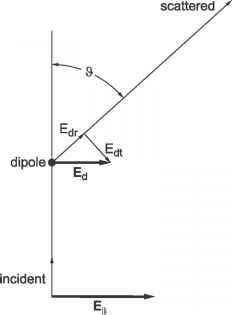
图7.9:一个入射电场(平面的图)激发一个平行的球对称偶极子场Ed分散。径向(r)和切向(t)组件的分散领域以不同的速率降低而增加距离。在足够大的距离(与波长相比),径向分量是微不足道的切向分量。
图7.9:一个入射电场(平面的图)激发一个平行的球对称偶极子场Ed分散。径向(r)和切向(t)组件的分散领域以不同的速率降低而增加距离。在足够大的距离(与波长相比),径向分量是微不足道的切向分量。
集中在偶极子。积分p2n pn
/ / Srr2罪tidtidp (7.112)
乔乔在这个球面,Sr的径向分量分散坡印亭矢量,辐射能分布在四面八方。因为周围的介质可忽视地吸收,这种能量是守恒的,因此Eq。(7.112)必须独立于r。这个需求被满足的充分条件是Sr r2成反比,在远场。这也意味着电场组件是成反比r。但是对于我们的目的,我们可以编写事件之间的关系和散射场组件.U !
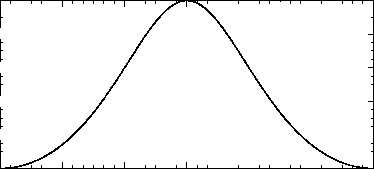
30 60 90 120
散射角(度)
图7.10:程度的光的偏振分散的球对称偶极子被非偏振光。
30 60 90 120
散射角(度)
图7.10:光散射的偏振度球对称偶极子被非偏振光。
C包含所有因素无关的偏振状态(但不是大小)的散射场。类似于r±, C因为r | |,所以情商穆勒矩阵具有相同的形式。(7.103):
±(cOS2t9 + 1)我(cos2ß- 1 0 0
我(cos2 - 1美元)(cos2 + 1美元)0 0
我们省略任何因素矩阵所有元素。的米勒矩阵散射粒子或分子通常被称为散射矩阵。
从情商。(7.114)由此可见,散射光的线偏振度,对事件非偏振光,
在图7.10所示。90°的散射角散射光偏振垂直于散射平面100%和超过50%极化片宽约70°。事件非偏振光的散射辐照度随散射角根据我(l + COS2ß)。
散射所描述的Eq。(7.116)不是各向同性,但等于向前和向后的半球。如果入射光散射偏振垂直于一个特定的飞机,在飞机的确是各向同性散射——但只有在飞机的方向,不是所有的方向。如前所述(5.2秒。),各向同性散射光并不存在,现在我们可以更好的理解为什么:光矢量波。
3.4节中我们简单的干扰参数,向前方向的散射应该增加速度与粒径比任何其他方向。在3.5节我们支持这些参数与计算领域。因为情商。(7.116)为球对称电偶极子显示等于向前和向后散射,我们可能会得出这样的结论:前进散射是从来没有低于向后散射。但是这里有一个例外,它是相关的术语“电”合格的偶极子(Ch缺席。3)。入射光也可以激发磁偶极辐射的分子或粒子与波长相比较小。一个电偶极子(2.6秒。)是大小两个费用相等,符号相反,它(电)偶极矩的大小电荷乘以它们之间的距离。磁偶极子是一个很小的电流环,其磁偶极矩电流乘以面积封闭的循环。通常情况下,磁偶极子辐射分子和小颗粒比电偶极辐射要小得多。一个例外是金属微粒在远红外线的频率。金属的导电性取决于频率,一般频率越低导电率越高。在低频率的高导电性,因此高电流,一个小金属球可能导致磁矩足够大产生磁偶极子辐射与电偶极辐射可比。此外,这两个偶极子域干涉的方式向前散射可以大大小于向后散射,几乎一个10倍。据我们所知,这对大气没有后果,但它至少也需要注意的一般规则的一个例外,向前散射最多大于或等于向后散射。总有例外,每一个规则,甚至总有例外的规则。
继续阅读:极化的天窗
这篇文章有用吗?