镜面反射的偏振

如前一节末尾所述，镜面反射可以改变光的偏振状态。考虑两个光学均匀的各向同性介质被一个光学光滑的平面界面隔开。严格地说，两种介质都应该是无限的，这样理论才适用，但是如果介质的尺寸比感兴趣的光的波长大得多，这个理想的(且无法获得的)条件就能得到很好的近似满足。波矢量为k的平面波;= - k(sin -±cos-;ez) (7.87)

从波数k的可忽略吸收介质(如空气)入射到界面上。该波产生(即激发)波向量为kr的反射波和波向量为kt的透射波:

基米-雷克南= - k (sin-rey - cos-rez), kt = kt (sin-tey + cos-tez), (7.88)

其中kt是发射介质中的波数。入射平面，我们认为是yz平面(图7.5)，由界面法线和入射线决定

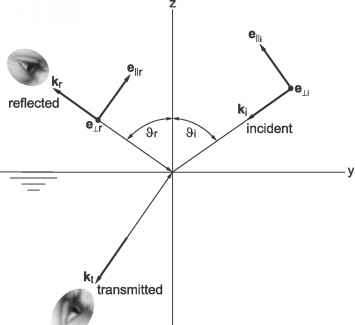
图7.5:平面波照亮光学均匀(无限)介质之间的光学光滑界面，产生(镜面)反射波和透射波(折射波)。

波向量。所有三个波向量都在入射平面上。而且，反射角等于入射角(镜面反射定律)。

= à， êt由折射定律(斯涅尔定律)给出。

其中m是折射率相对于入射介质的透射介质。因为m可以是复数，所以可以是折射角，但是这个复数角的实部不是折射角，折射角定义为复数波向量的实部与界面法线之间的夹角。当m为复时，透射波是非均匀的(除了正常的发病率， = 0):复波向量的实部和虚部不平行。

不管你在别处看到的是什么，这里Snel的拼写是正确的。无论斯内尔凭经验发现了折射定律(这一定律一直存在争议)而名声大好，他的名字被拼错的次数可能比历史上任何其他科学家都要多。基尔霍夫可能紧随其后。一个复活的斯内尔，在数百本教科书和数千篇论文中看到他的名字时，可能会惊呼:“这是什么1!”而基尔霍夫的反应可能是:“h在哪里?”

入射和反射电场分量是相对于平行和垂直于入射平面的正交基向量指定的(图7.5)，定义这样x e||是在波向量的方向上。注意，入射场的平行基向量与反射场的平行基向量是不同的。反射场相对于入射场的复场分量为

Ei|r m cos - cos tan($i - $t)

11 E||i m cos + cos$t tan($i + $t)

r= - = - =——(l.yL)

E±i cos + mcos $ tsin (^i + $t)'

其中下标I和r分别表示入射和反射。式(7.91)和式(7.92)为菲涅耳系数。在光的电磁理论发展之前(菲涅耳死于1827年)，它们规定了任何入射角度和被照射介质的反射场的振幅和相位。两个正交偏振态对应的反射率为

R = | R |||2， = |f±|2。(7.93)

潜在的方程式。(7.91)和式(7.92)是附加的假设，即两种介质在感兴趣的波长处都是非磁性的。在正入射(^ = 0°)时，两个反射率相等，

在掠入射(^ = 90°)时，对于任意m，两者均为1。但对于所有中间入射角，两者是不同的，例如，可见光照射的空气-水界面(图7.6)。特别是，当n时，R| =0，而R±对于任何入射角都不消失。由式(7.90)可知式(7.95)等价于tan ^ = m (7.96)

式(7.96)只能严格满足m实。

由于式(7.96)满足的入射角R| = 0，在此角度反射的非偏振光垂直于入射面为100%线偏振。这个角被称为极化角或布鲁斯特角，以纪念大卫·布鲁斯特爵士，他是第一个凭经验发现这个角的人。布鲁斯特的论文发表于1815年，流传已久。这本书以一种几乎在今天的科学写作中被禁止的清晰方式，以对艾蒂安-路易斯·马卢斯的感人致敬结束，他在1809年发现了偏振反射，并创造了这个术语

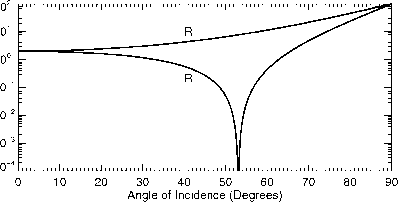
图7.6:平行于入射面偏振光(||)和垂直于入射面偏振光(±)的可见光波长水的反射率(n = 1.33)。

通过(错误的)用磁极来类比偏振，但没有认识到布鲁斯特后来阐明的规律:“折射率是偏振角的正切。”布鲁斯特测量了十几种透明物质的极化角度，并将其从正切方程中计算出来的值进行了比较，发现平均一致，在15'以内。但布鲁斯特知道他并没有推导出这个方程:“在这些研究中，我没有使用假设性假设……偶尔也使用理论的语言，但由此引入的术语仅仅是对实验结果的表达。当发现积累了更多的事实，并把它们与一般规律联系起来时，我们就可以安全地开始研究了。来推测光在各种变化下所表现出的奇妙现象的原因"菲涅耳又等了几年，麦克斯韦又等了半个世纪。

在一篇题为《布鲁斯特会承认今天的布鲁斯特角度吗?》的论文中，Akhlesh Lakhtakia批判性地研究了布鲁斯特角度这个术语在今天的使用方式。在现代教科书中，它最常被定义为R\\ = 0，但布鲁斯特不知道这一点，对他来说，现在以他的名字命名的角度是入射角(偏振角)，在入射无偏振光的情况下，反射光完全线性偏振。此外，Lakhtakia还证明了存在各向同性介质，其平行分量的偏振角和零反射角是不相同的。

有时你会遇到这样的论断:金属的反射不会使入射的非偏振光发生偏振。虽然当m的虚部不可忽略时，式(7.96)没有实解，但金属确实表现出一个反射角，有时称为伪布鲁斯特角，在这个角上极化程度最大。而且它可以高得惊人，远远超过50%，特别是对于反射率低于银和铝等导电金属的金属(如铁和铬)。误解金属反射的光是无偏振的一个原因是伪布鲁斯特角通常是在10°左右的掠入射。

关于偏振的另一个误解是，白炽体发出的光是无偏振的，这可能源于黑体(不存在的)发出的辐射是无偏振的。考虑空气中的一种光学光滑均匀的介质，其厚度足以使透射可以忽略不计。在此假设下，发射率为1 -反射率(见第1.4.1节)，由于反射率取决于极化，因此发射率也取决于极化:

£|l = 1 - R\\， eL = 1 - Rl。(7.97)

这两个发射率对于正方向和掠方向是相等的，但是对于真实物体在所有中间方向上是不相等的。对于黑体(R| = Rl = 0)，两者在所有方向上均为1。

虽然这一节的重点是镜面反射时的偏振，但由于相对容易观察，偏振的状态入射辐射也可在传输时进行更改。反射菲涅耳系数，式。(7.91)和(7.92)，并伴有两个传输:

E^ icos -;+ mcos -t这里的下标t表示传输。

继续阅读:偶极散射天窗极化

这篇文章有用吗?

0 0