偏振光的本质

你看到对物理现象的解释或关于物理现实的陈述次数越多，尤其是以不变的咒语的形式，尤其是在没有任何限定条件的教科书中，你就越能确定它是错误的。更简洁地说，重复增加了错误的可能性。这是一条几乎普遍适用的定律。一个例子是断言光波的电场和磁场总是彼此垂直，并与传播方向垂直。因为这种断言已经被不加限制地多次提出，所以你可以肯定它是错误的。事实也的确如此。你可以去问任何一个对近景有所了解的电气工程师。在第4.1节中，我们注意到Poynting向量

基础大气辐射:有400个问题的导论。Craig F. Bohren和Eugene E. Clothiaux版权所有©2006 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim ISBN: 3-527-40503-8

的大小和方向能源运输在任意点被任意电磁场。电场E和磁场H都必然垂直于S，尽管它们不一定相互垂直，也不一定垂直于传播方向(如果它指的是固定相位表面的法线)。例如，在一个被照亮的球体(实际上，任何粒子)内的场都不相互垂直，而且恒定相位表面的概念是没有意义的。被球体散射的场彼此之间也不垂直，除非大约在足够大的距离上(与波长相比);恒相曲面的概念有其局限性。我们所能确定的只是电场和磁场位于一个与波印亭矢量垂直的平面上。通过电场来指定电磁波的极化特性已经成为习惯，尽管磁场也可以起到同样的作用，你偶尔会看到一些作品(尤其是英国作家的作品)，其中极化是基于磁场的。

7.1.1振动椭圆及椭圆测量参数

此时我们唯一的假设是电场是时谐的:

其中E为电场的复表示(见第2.5节)。然而，要指定E的偏振态，我们需要实场。因为E位于垂直于S的平面上，所以只需要两个分量。我们表示两个正交的单位向量as和e||，使x e||在Poynting向量的方向上。当我们讨论为什么坐标轴被表示为垂直(±)和平行(||)的应用时，这将变得很明显。场分量是的实部

E±=±exp{我(^ + ut)}, E \ \ = \ \ exp {- i (tf | | + ut)}, (7.3)

振幅a和相位tf是实函数，可能取决于位置而不是时间。在不丧失一般性的情况下，我们可以将振幅视为正的，因为由于相位的关系，场分量可以为负(即，cos n = -1)。

在空间中的一个固定点上，电矢量的尖端(坐标由E±和E|的实部给出的点)无穷无尽地勾勒出一条封闭的有界曲线。当两个相位相等时，这条曲线是一条斜率等于振幅之比的直线。当相位相差n/2时，曲线是一个主轴沿坐标轴对齐的椭圆，其中两个半轴的长度是，当这两个振幅相等时，结果是一个| . a圆。

一般来说，式(7.3)描述了任意椭圆度的任意方向椭圆(不要与偏心率混淆)，定义为长轴与长轴长度的比值(图7.1)。这个振动椭圆的方位角是主轴和参考轴(例如，其中一个坐标轴)之间的夹角。振动椭圆的另一个椭偏参数是它的旋向性，即它在时间上被描摹出来的旋转意义。对于什么是右旋和左旋，没有普遍的约定。此外，某一特定领域的研究人员通常认为每个人都知道他们的惯例是什么，所以觉得没有必要说明它。如果振动椭圆被跟踪，我们采用将场称为右手场的惯例

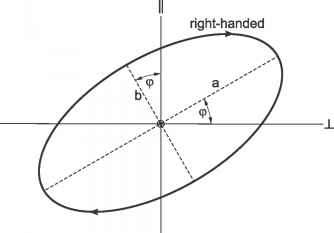
图7.1:时谐电场描画出一个由其旋向、方位角和椭圆度b/ A指定的椭圆。

顺时针向外，就像想象的那样，看到了波印亭向量。按照这种惯例，在空间中由电场矢量尖端勾勒出的螺旋就是全世界都称的右手螺旋。

式(7.3)所描述的电场是100%或完全极化的，因为它有一个确定而固定的振动椭圆。完全偏振的一般状态是椭圆，特殊情况是线性和圆形。但是一些教科书，甚至更多的科普书籍，传达了这样一种概念，即极化意味着线性极化，没有其他类型的极化是可以想象的。更糟糕的是，线偏振光有时被称为平面偏振光，特别是在旧的作品中。从几个方面来看，这是一个糟糕的术语选择。如果一个平面电磁波[式(7.4)]是线性极化的，我们就会有一个尴尬的名称——平面极化平面波(并且极化平行于或垂直于另一个平面)。第一个平面由电场矢量和传播方向定义(等效地，电场在传播过程中勾勒出的平面表面)，第二个平面是恒定相位的曲面。为了保持一致，我们必须将椭圆偏振光描述为椭圆-螺旋面偏振光，因为它的电场在空间中沿椭圆螺旋面走。然而，这是不必要的，因为平面波(事实上，任何波)的偏振状态是由椭圆偏振参数指定的，而椭圆偏振参数与曲面无关。

我们的经验是，那些在易受影响的年龄就被教育光是平面偏振光的人，会发现很难理解椭圆偏振光，更难理解部分偏振光。事实上，他们有时会混淆非偏振光和圆偏振光。然而，要理解部分偏振光，首先要牢牢把握完全偏振光。这种光的基本性质是电场的两个正交分量之间的完全相关。它们可能在时间上波动，但如果它们同步波动(即振幅之比和相位差一样是恒定的)，振动椭圆就具有确定和固定的形式。当两个正交分量之间存在偏相关时，产生部分偏振光;当没有相关性时，就会产生无偏振光。

我们知道偏振的存在，只是因为两束光，除了一个或多个椭圆度参数(椭圆度、方位角、偏手性)外，在所有方面都相同，可以以明显不同的方式与物质相互作用。如果不是这样，时谐场的偏振态将是一种无功能的装饰，就像1959年凯迪拉克的机翼一样。当场与物质相互作用时，只会发生两件事:振幅或相位(或两者都改变)。如果电场的两个正交分量改变不同，极化状态就会改变。这里的“改变”是指入射(或激励)波的偏振状态与它引起的波的偏振状态不同。

7.1.2正交极化波无干涉

一般平面谐波(复)波具有如下形式

其中E0在空间和时间上是常数，波向量k可以是复数;磁场H由类似的表达式给出。这些场必须满足其中C是频率相关的参数(如果传播介质是吸收的，可能是复杂的)，波在其中传播的介质的特性;它的价值在这里无关紧要。记住k的实部和虚部不需要互相平行;即等相位曲面与等振幅曲面不重合(见问题7.52)。如果是这样，波就称为齐次波;如果不是，则是非齐次的。不均匀的波浪不是不受约束的想象力的产物。它们可以很容易地通过光照吸收介质而产生倾斜入射．只有当一个波是齐次的，也就是说，它的波向量具有k = k e的形式，其中k可以是复数，但e是一个实单位向量，(实)电场和磁场才垂直于传播方向e。只有当k为实数时，电场和磁场才相互垂直。从现在起，除非另有说明，我们假设感兴趣的波是齐次的(k = k e)，它们传播的介质是非吸收的(k是实数)。绝对不存在平面波和非吸收介质。我们可以不去假设它们这样做，因为偏振的测量几乎总是在可忽略不计的吸收介质(例如，空气)中进行的，并且在距离有限源(例如，有界散射体)足够大的距离(与波长相比)上，它们发出的场在探测器上大致是平面的。但是，如果我们要研究波在吸收介质中或在接近源的地方的极化问题，下面的许多分析将不能严格适用。

根据上一段的假设，Poynting向量为k•E = 0, H = Ck x E, k•H = 0，

由公式得出。(7.1)和(7.5)和同一性

式(7.6)是对第3.3.2节结果矢量波的推广，即标量平面谐波(在弦上)的能量传播与波函数的平方和成正比。为了避免混乱的符号，我们不使用不同的符号来表示字段及其复杂的表示形式，而是相信上下文可以指示其含义。

如果两个平面波的旋向相反，且振动椭圆的方位角垂直，则称它们为正交极化。正交极化波不干涉，因为它们的和的波印亭矢量是它们的波印亭矢量的和。为了证明这一点，考虑两个这样的波:

Ei = a\ cos wt e|| + b\sin wt e^， E2 = b2 sin wt e|| + a2 cos wt e^， (7.8)

其中aj和bj是正的，但其他情况都是任意的。这两个波的和对应的波印亭矢量为

S = Ck[(ai + a2)cos2 wt + (bf + b2)sin2 wt + 2(a1b2 + a2b1) sinwt cos wt]。(7.9)

如果两个场在E1•E2 = 0的限制意义上是正交的，则a1b2+a2b1 = 0，且波在任何时刻都不干涉。无论它们的正交偏振状态如何，时间平均Poynting向量都是可加的，因为(sinwt cos wt) = 0:

我们通常对波的周期(逆频率)大倍的平均波印亭矢量感兴趣。虽然式(7.1)中的字段必须是实数，但我们可以直接从字段的复杂表示中确定时间平均Poynting向量:

这个方程对任何时谐电磁场都成立。一个更有限的版本，只适用于平面均匀波在非吸收介质，是

这个等式是接下来内容的核心。

7.1.3 Stokes参数和椭偏参数

虽然我们可以想象观察一个以1015赫兹旋转的电矢量的尖端，但认为我们真的可以这样做纯粹是幻想。我们所能测量的，通常是时间平均辐照度。因此，对Poynting矢量大小的测量必须是通向椭圆参数的路径，并且假定式(7.3)是椭圆方程，它们必须仅依赖于振幅a«和a±_以及相位fin和

从方程式。(7.3)和(7.12)光束的时间平均辐照度，在这里用I表示，是振幅的平方和

I = |(S)| = E\\E\\ + E±E*±= a2 + a\。(7.13)

这个方程中缺少一个常数因子，我们在这里忽略它，因为确定椭圆测量参数不需要绝对测量。为了获得独立的振幅，我们需要一个理想的线性偏振器(或线性偏振滤波器)的帮助。这种滤光片完全透射特定方向上的线偏振光，但不透射正交方向上的线偏振光。顾名思义，理想的线性偏振器是不存在的，但我们可以接近，至少在有限的波长范围内。一个例子是用于偏光太阳镜或相机偏光滤镜的薄板偏光片(其功能将在第7.4节中解释)。这样的片材偏振器对nd c1的吸收是不对称的，其中k是吸收系数，d是片材厚度，对于沿传输轴线偏振光，而nd > 1是垂直于该轴线偏振光。在可见光和近可见光波长，这种吸收系数的差异是薄片材料在分子尺度上各向异性的结果。我们看不到传输轴，虽然我们可以看到微波辐射的偏振滤波器的传输轴。对于不同的正交线性偏振态，具有不同吸收系数的介质称为线性二向色介质。

现在我们想象在光束中插入一个理想的线性偏振滤光片，并测量传输的辐照度，首先是传输轴沿e||，然后沿e±_，然后减去这两个辐照度:

Q = E\\El - E^E*±= aj - a2±。(7.14)

我们现在已经做了足够的工作来得到振幅:

相呢?从方程式。(7.3)和式(7.12)看来，要得到相位，我们必须将电场的两个正交分量都透射一点。例如，如果我们将一个线性偏振滤波器与它的透射轴以45°与e j对齐，则透射振幅为

将滤波器旋转90°，透射振幅为

对应于等式的辐照度之差。(7.16)和(7.17)为

U = E\\E*±+ E±_Ej =2a，|a±cos S， (7.18)

测量I, Q和U足以得到cos S，但因为cos S = cos(-S)不足以确定波的手性。给定cos S，我们不能说S是正的还是负的，这决定了用手性。要找到这个量需要理想的圆偏振光器(或圆偏振光滤光片)的帮助，这种设备完全传输单手偏振光，但不传输反手偏振光。这种圆形偏振器比线性偏振器更难找到。对于圆偏振光的不同状态，存在具有不同吸收系数的介质，称为圆二向色介质。例如，我们的身体和所有有机物质都充满了螺旋分子(例如DNA的双螺旋结构)，而螺旋在它们的镜像上是不可叠加的:一个右旋螺旋的反射是一个左旋螺旋。由于这种镜面不对称，我们期望这种分子在不同的圆偏振状态下的吸收是不同的。事实的确如此，但通常在紫外线频率上差异最大，而且很难找到吸收系数相差很大的介质。然而，我们可以想象用理想的圆形偏振器进行思想实验。

为了讨论圆偏振光，可以方便地引入一组复基向量:

eR = + eL = ~ (7-19)

它们是标准正交的，其中eR•eR = 1, eL•eR = 1, eR•eR = 0。(7.20)

eR对应单位振幅的右圆极化波，eL对应单位振幅的左圆极化波。因此可以写成任意电场

其中圆偏振(复)振幅与线偏振振幅的关系是

Er = - iE±)，El = - l(£7|| + iE±)。(7.22)

现在想象一下，在光束中插入一个理想的右圆偏振器，测量透射的辐照度ERER，然后测量理想的左圆偏振器透射的辐照度ElEL，用第一个辐照度减去第二个辐照度:

V = er - ELEL =我(E ^ E *±- E±E * \) = 2 ^ ^ ^} = 2 ^±罪。(7.23)

知道sins和cos S我们可以确定S的符号，从而确定波的旋向。

这四个量{I, Q, U, V}只不过是辐照度的和和差，被称为斯托克斯参数，由乔治·加布里埃尔·斯托克斯爵士于1852年首次提出。甚至在150多年后，他的论文《论河流的组成和分辨率》

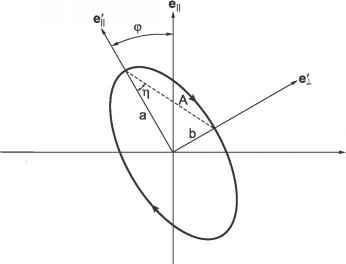
图7.2:未启动坐标系相对于启动坐标系旋转，启动坐标系的轴沿振动椭圆的长轴b和长轴a。

来自不同来源的偏振光”仍然值得一读。您可能会遇到Stokes参数的不同符号(他使用了A、B、C和D)， Stokes参数的线性组合也是有效的Stokes参数。它们有时被简洁地写成列矩阵

/	我	＼
	问
	U
V	V	）

EnE* + ElEl E\\E*\ - El EnEl + ElE* y i(E\\E*±- EE)

EnE* + ElEl E\\E*\ - El EnEl + ElE* y i(E\\E*±- EE)

称为Stokes向量，尽管它没有与固有向量相同的权利和特权。例如，Stokes参数在这里不是独立的

12 = q2 + u2 + v2

斯托克斯的论文比麦克斯韦著名的电磁光理论发表早了十几年，比波印廷的作品发表早了32年。甚至在光波完全建立在一个充分的理论基础之前，关于光波的性质就已经知道了很多。

现在我们必须证明斯托克斯参数决定椭圆度参数。在接下来的内容中，字段是真实的。式(7.3)中场的实部可以用角和余弦的恒等式展开，并写成矩阵形式为

An cos fin -an sinaj_ cos -a±sincoswt sinwt

在一个坐标系中，场的分量是

E' = a cos wt, E'±= b sin wt， (7.27)

场画出一个右旋椭圆，小轴b，长轴a(如果a> b)，这是从求解式(7.27)cos wt和sinwt，然后平方和相加。从原始坐标系到初始坐标系的变换为(图7.2)

E«\ = (cos y sin y \ / E«E±J y - sin y cos y / \ E'±

a cosyb siny \ i coswt -a sinyb cosyjysinwt

等式的相等性。(7.26)和(7.28)要求a«cos = a cos y， (7.29)

将这些方程的左边平方并相加，使结果等于右边的平方和:

a«+ a\ = a2 + b2 = I. (7.33)

其中0 < n < n/4且tann = b/a。现在将Eq.(7.29)乘以Eq. (7.30)， Eq.(7.31)乘以Eq.(7.32)，将结果相加，并使用角和的正弦和余弦恒等式:

U = 2a«a±cos S = (b2 - a2) sin2y = - a2 cos2nsin2y。(7.35)

现在是平方方程。(7.32)和(7.30)取其差，平方式。式(7.29)和式(7.31)，取其差，最后取结果的差:

A \ - ajj = (b2 - a2) cos2y， (7.36)

的收益率

Q = a2 - a\ = a2 cos2n cos2y。(7.37)最后，将等式相乘，得到V。式(7.29)和(7.32)，(7.30)和(7.31)，相加得到ana±sin S = ab， (7.38)

由式(7.34)得到的

如果我们对左圆极化波进行相同的步骤，I、Q和U不变，而V变了

对于左圆偏振光和右圆偏振光，我们不需要单独的一组方程，我们可以让n在(-n/4, n/4)范围内将它们组合起来，其中负角对应左圆偏振光，正角对应右圆偏振光。概括:

I = A2, Q = A2 cos2ncos2y, U = -A2 cos2nsin2y, V = A2 sin2n， (7.41)

其中0 < y < n和-n /4 < n < n/4。因为tan2y不能唯一地决定y，我们需要额外的信息:如果U < 0,0 < y < n/2，而如果U > 0, n/2 < y < n。从式(7.41)可以得出，I和V不依赖于坐标系(即y)， Q和U依赖于坐标系，但它们的平方和不依赖于坐标系。

平面波式(7.4)的恒相面和恒幅面在范围上是无限的。因此这个波的电场占据了所有的空间，当然，这在物理上是不现实的。要将上述分析应用于横向有限的实际梁，其特性必须具有横向均匀性。斯托克斯参数[式(7.24)]是通过思想实验得到的，这些实验很容易陈述，但在实践中并不容易做到。然而，一旦我们知道了这些参数的形式，我们就可以设计出可行的方法，用现成的线性缓速器和偏振滤波器来测量它们(见本章末尾的问题7.36)。

7.1.4非偏振光和部分偏振光

由式(7.2)或式(7.3)所描述的电波必然是完全极化的，因为它的振动椭圆从开始到时间结束都具有单调的规律(实际上，这个时间间隔不需要跨越永恒，只是比波的周期长得多)。微波辐射或者无线电天线可能非常符合这种描述，因为天线是一个相干物体，它的各个部分相对固定(在波长的尺度上)，由或多或少的时间谐波电流驱动。制造一个不辐射完全极化波的微波或无线电天线需要一些独创性。然而，波长短得多的辐射通常来自大量彼此或多或少独立发射的微小天线(分子)阵列，因此我们不会期望来自这些来源的辐射具有相同程度的规律性。不规则性的极端例子是无偏振光，而不规则性的极端例子是完全偏振光，这两种理想化在自然界中从未严格实现过。但是什么是非偏振光呢?

也许定义这种光的最简单的方法是操作上的，受制于前面关于理想线性和圆形偏振器的警告。我们可以设计什么样的实验测试来确定一个光束是否是非极化的?假设我们通过一个理想的线性偏振器传输它，并发现不管它的传输轴的方向如何，传输的辐照度是相同的。这意味着电场没有首选方向，因为如果有，辐照度就会变化。根据我们对斯托克斯参数的操作定义，该光束的Q = U = 0。但是等等!圆偏振光束也会产生同样的结果。所以我们现在要确定光束是否表现出偏向性。首先将光束通过一个理想的左圆偏振器，然后通过一个右圆偏振器。如果两个透射的辐照度相等，则V = 0，光束的电场对左旋不偏向右旋。 Thus our operational definition of unpolarized light is that for which Q = U = V = 0. The Stokes parameters of partially polarized light also do not satisfy Eq. (7.25) but Q, U, V are not all zero.

通过将式(7.3)扩展到具有(真实)电场分量的准单色辐射，我们可以在这些骨架上添加更多的理论血肉

\ \ E (t) = a \ \ (t)因为{$ | | (t) + wt),埃尔(t) = a±(t)因为{tf±(t) + wt), (7.43)

其中振幅和相位现在随时间变化，但比cos wt慢得多。在此限制下，电场式(7.43)及其相关磁场大致满足式(7.5)。式(7.43)对应的瞬时Poynting向量为

其大小(在一个常数因子内)为

|S| = (a| cos2 -&H + a\ cos2 -i)cos2 wt

+(a| sin2 - + al sin2) sin2 wt (7.45)

-2 (a| cos-1| sin+ al cos-1 sin -i) sin wt cos wt，其中振幅和相位可能取决于时间(不明确，以保持符号整洁)。要确定式(7.45)的时间平均值，需要计算该形式的积分

- / f(t) cos2 wt dt， - / g(t) sin2 wt dt， - / h(t) sinwt cos wt dt。(7.46)

tj tj tj tj 0

我们只需要考虑第一个积分因为它为其他两个积分提供了模式。将积分范围分成N个相等的区间

(/ cos2 wt) = - f(t) cos2 wt dt = - Y / /(t) cos2 wt dt。(7.47)

tj0 i= 1jti

由积分学的中值定理

I f(t) cos2 wt dt = f(fi) / cos2 wt dt, ti Jti

其中U < U < U + At。根据准单色光的定义，我们可以选择At»1/uj，使得f(t)在这个时间间隔内近似为常数[称为值/(¿¿)]，因此余弦平方的积分近似为At/2，时间平均值近似为

同样的,

(ffsin2 cut)»gjtj)， (h sin cut cos cut)«0。(7.50)

从方程式。(7.45)，(7.49)，(7.50)因此，准单色光的时间平均辐照度为

I = (|S|) = (a\ + a\) = (E«E| + E±E*L)。(7.51)

和前面一样，省略了所有公因数。由于斯托克斯参数是辐照度的和和差，因此这种光的其他三个参数由类似的表达式给出:

Q = (E|| E\ - E±El) = (ajj - a2±)，(7.52)

U = (En E*±+)= (2ap a±cos S)， (7.53)

V =(¿EEl - E^E^)) = (2apa±sin S). (7.54)

准单色光束的一个例子是经过普通滤光片(相对于偏振滤光片)的准直阳光，滤光片是一种只在一个频带上传输光的装置。这种透射光的光谱宽度可能很窄，但其正交场分量的幅值和相位随时间波动，与周期比大，与探测器响应时间比小。

根据式(7.42)，椭偏参数仅依赖于斯托克斯参数的比值，这反过来意味着它们仅依赖于振幅a|和相位差S = -假设这些振幅和相位在时间上波动，但是同步的，也就是说，它们是相关的，振幅和相位差的比值在时间上是常数。然后由等式得出。(7.51)-(7.54)表明12 = Q2 + U2 + V2，因此尽管有波动，光是完全偏振的。相关性是理解偏振光所必需的。完全相关对应于完全偏振光，与非偏振光不相关，与部分偏振光偏相关。

我们可以将式(7.43)形象化如下。在几个周期的时间间隔内，电场矢量勾勒出一个或多或少确定的振动椭圆，但随着时间的推移，振动椭圆发生变化。如果在探测器的响应时间内描摹出所有振动椭圆，则光是非偏振的。

7.1.5极化程度

任何具有Stokes参数I, Q, U, V的光束都可以被认为是两个光束的非相干叠加，一个是非偏振的，一个是完全偏振的:

在哪里

Ip = Q2 + U2 + V2。因为Ip < I，所以(但请参阅问题7.27)

Q2 + u2 + v2 < i2，

对于完全偏振光，等式成立。我们将光束的(椭圆)偏振度定义为偏振部分的辐照度与总辐照度的比率:

通常乘以100并表示为百分比(< 100%)。

我们可以进一步想象，这束光是三束光的叠加，一束非偏振，一束线偏振，一束圆偏振:

Iu 0

在哪里

/ip = VQ2 + u2， /cp = \v\。这自然导致定义线偏振度hp = VQ2 + U2 I I

和圆极化的程度

Ic cp I

一个有符号的量:正值对应右圆极化，负值对应左圆极化。

为了确定光束的线偏振度，在其中插入一个理想的线偏振器，并测量透射光的辐照度。假设偏光器的传动轴与en轴成一个角度£(在0和n之间)。沿这条轴的透射振幅为

其中下标I表示入射场的分量。因此，这个透射场的分量是

E±t = E||i sin£cos£+ En cos2£，(7.64)

elt = E||i sin2£+ Eni sin£cos£。(7.65)

由这些方程和斯托克斯参数的定义可以得出透射辐照度为

它的最大值和最小值出现在tan2£=- ^。(7.67)

式(7.67)的两个解之间以n/2分隔。在不丧失一般性的情况下，我们可以将Ui和Qi设为正，在这种情况下，最大值出现在余弦为负，正弦为正时，而最小值出现在余弦为正，正弦为负时:

/max = ^ (Ii - Qi cos 2£+ U{sin20， (7.68))

其中£是Eq.(7.67)的解，其余弦为负。减去这两个方程，把它们相加，然后取它们的比值:

/max ~ /"min _ COS 2£+ Uj sin 2£T 4- T■T

根据式(7.67)我们可以写出

Qi = -Acos2£，Ui = Asin2£，(7.71)

在哪里

这就产生了

继续阅读:t7 T IJi

这篇文章有用吗?

0 0