天空的颜色和亮度的变化
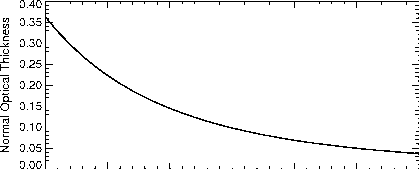
选择性散射分子的必要但不充分是一个蓝色的天空。大气中也必须光学薄,至少对于大多数天顶的角度。黑暗的空间作为背景是理所当然的而且是必要的,莱昂纳多认可。图8.2显示了正常标准大气散射光学厚度与波长。
400 450 500 550 600
波长(nm)
图8.2:正常标准大气散射光学厚度。从Penndorf (1957)。
400 450 500 550 600
波长(nm)
图8.2:正常标准大气散射光学厚度。从Penndorf (1957)。
从二束近似(Eq。(5.66)]与g = 0(分子散射)向下扩散的辐照度D ^头顶的天窗在表面
D 1, F0是事件辐照度和Tn是正常的光大气的厚度。Tn C这个接近1
方程(8.1)和(8.2)是一个黑色的下垫面(零反射率)。另一个极端,一个白色的下垫面(1)的反射率?我们可以通过解决Eq。回答这个(5.49)=向下和向上的辐照度的表面。但这是更好的为我们的灵魂(即。,我们的物理直觉)如果我们想这一定是情商约两倍。(8.2)因为空气被两个近似等于来源:直接和反射太阳光。从图8.2可以得出这条件情商的有效性。(8.2)是满意的。因此天窗大气分子的光谱应该的太阳光谱调制的瑞利散射法,实际上是头顶的天空(图8.1)。什么另一个极端,地平线的天空?要回答这个使我们考虑空气光。
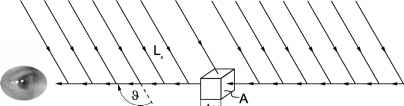
唯一真正区分空气光和天窗是空气光的背景可以是有限的对象在一个有限的距离,而天窗的背景是几乎空无一人,无限的空间。因为空气光,光散射的分子和粒子沿着视线从观察者对象,甚至是一个本质上的黑色物体发光。考虑一个水平统一制服的视线受到阳光的照射(图8.3)。表示由L0太阳的光辉照亮了视线。太阳辐照度的方向
Ax x
7777777777777777777777777777777777777777777
图8.3:一个观察者看着远处的黑色物体然而收到一些散射的光,因为所有的分子和粒子沿着视线。
L0Qs,认为立体角对应着太阳。假设地面反射的可以忽略不计。光分散向观察者单位立体角的分子和粒子体积小AAx距离x因此L0Qs (3 axap (e),(3)散射系数和p (e)的概率是单位立体角方向散射的e。除以一个,这是垂直于视线,获取贡献AAx的光辉。这是光辉散落在x向观察者,需要乘以透光度exp (- (x)获得这个光辉的一部分由观察者接收。总辐射的散射结果一切都沿着视线观察者和一个黑色的对象之间的距离d的积分在t = [3 d光学厚度沿路径d和两个几何因素集中到一个单一因子G = Qsp (&)。潜在的Eq。(8.3)是假设光散射的视线不是又分散在这个方向,这是一个好的假设如果光学厚度方向外侧视线很小(它是清晰的气氛而不是雾)。
只有在限制t ^ 0 L = 0和一个黑色的物体是黑色的。对于t c 1, L«L0Gt。在纯粹的分子的气氛中t随波长根据瑞利定律,因此遥远的黑色对象被认为是蓝色的。随着t增加那么L但不是比例:路径越长,散射的数量越大,而且衰减就越大。L的极限值([L0G d > 1),源的辐射光谱,照明的视线不管(波长的依赖关系。这个结果应该结束废话的白色地平线的天空绝无错误的信号散射的“大颗粒”。
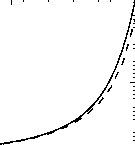
虽然分子光学厚度在地球大气层的可见小沿径向路径,路径不再是如此接近或沿着地平线。光学
角(度)
图8.4:纯大气分子散射光学厚度与规模高度8公里地球上相对于正常的光学厚度范围的天顶角度接近地平线。实线是统一的气氛近似;的虚线是成倍地减少散射系数。
厚度沿任意路径积分:
道路的表面制作一个常数天顶角©与大气的垂直方向散射的指数递减密度,Eq。(8.4), R是地球的半径,H分子数密度(即规模高度。,数密度减少的速度指数随高度),和海平面的散射系数。径向(正常)路径(©= 0)Eq(8.5)可以集成获得
因此正常的大气光学厚度的数密度散射减少指数随高度是一样的,统一的有限厚度H的氛围。
尽管情商。(8.5)不能综合分析任意天顶角,制服,有限的大气近似
非常好的到地平线(©= n / 2),见图8.4。考虑到分子数密度的指数降低收益率较低的光学厚度最多10%。平坦地球是一个有着无限R, Eq。(8.7)的收益率预期的关系
切向(层)的光学厚度(©= n / 22)从情商。(8.7)是好的近似
因为2 r / H > 1。为R = 6400公里和H = 8公里,Tt = 40 t„。
暗物体的亮度和颜色的变化随着距离被称为空中透视达芬奇的作品。通过它,我们无意识地估计距离未知大小的对象,比如山脉。空中透视与天空的颜色和亮度的变化与天顶角。虽然光学厚度沿着地平线路径也不是无限的,它是足够大(无花果。8.2和8.4)GL0是一个很好的近似的光辉地平线的天空。为各向同性散射,几乎满足分子(见7.3秒。),G是大约10 ~ 5,立体角的比例认为太阳的立体角方向(4 n)。因此地平线的天空不是那么明亮的阳光直射。
与5.2节中描述的牛奶实验,观察当看什么地平线的天空不是用散射光(多)。白色的牛奶和地平线的天空有其起源在多次散射,但以不同的方式体现。牛奶是白色的,因为它是弱吸收和光学厚,因此所有组件的事件白光将分散到观察者即使紫色和蓝色组件遍历一个较短的平均路径的牛奶比橙色和红色组件。白色层光已逃脱了被用分散,尽管多个散射是为什么这个灯是白色的(严格来说,源的频谱)。更多的光在短波长比在一个极端长波最终分散向观察者,在情商就证明了这一点。(8.3)。但是长波长光的大概率被传送到观察者而不被分散的视线,就是明证exp(3 ^)在Eq。(8.3)。足够长的光路,这两个流程的补偿,导致地平线光辉的来源。
手里拿着Eq。(8.3)我们可以尝试估计比地平线光辉的顶点(开销)的光辉。如果我们把入射光直接近地平线(切线)辐射大约是开销
Lt = LoQsP (90°) {1 - exp (tt)}«Lo ^ sp (90°) (8.10)
和天顶光辉大约是
Ln = Lo ^ sp (0°) {1 - exp (Tn)}«Lo ^ sp (0°) Tn, (8.11)
P是分子散射相函数和Lo是大气外的光辉。所有我们需要的是两个散射相位函数的比值的方向,
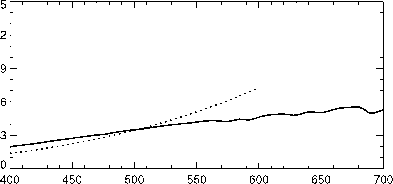
图8.5:测量比地平线(实线)的辐射和太阳辐射直接开销高在天空晴朗的日子在州立大学,宾夕法尼亚州。虚线是比简单的纯理论预测的分子的气氛。
波长(nm)
图8.5:测量比地平线(实线)的辐射和太阳辐射直接开销高在天空晴朗的日子在州立大学,宾夕法尼亚州。虚线是比简单的纯理论预测的分子的气氛。
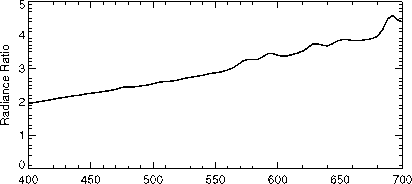
图8.6:光谱辐射的测量比氧化镁(分别)粉被日光光谱辐射的地平线的天空在晴朗的天在州立大学,宾夕法尼亚州。
波长(nm)
图8.6:光谱辐射的测量比氧化镁(分别)粉被日光光谱辐射的地平线的天空在晴朗的天在州立大学,宾夕法尼亚州。
我们从情商。(7.117)。结果是惹恼,SJ2)
尽管衰减的阳光照亮方程式的视线是被忽视的。(8.10)和(8.11),当衰减包含情商。(8.12)是不变的。还p(0°)并不意味着

500 550 600
波长(nm)
图8.7:光谱的头顶的天窗二束理论分子大气光学厚度(实线),这个厚度(虚线),10倍和40乘以这个厚度(虚线)。
500 550 600
波长(nm)
图8.7:光谱的头顶的天窗二束理论分子大气光学厚度(实线),这个厚度(虚线),10倍和40乘以这个厚度(虚线)。
太阳直接开销和视线直接朝向太阳,而是太阳高挂在天空,散射角,小于10 - 20°。情商的有效性的证据。(8.12)显示在图8.5中,测量的比率光芒的地平线,头顶的天空,太阳高挂天空,晴朗的日子。协议与情商比率测量与计算。(8.12)使用普通光学厚度图8.2是出奇的好。此外,长波长的分歧是预期的方向:正常的光学厚度几乎总是比纯粹的大气分子甚至在一个非常干净的环境。
通过大气光学厚度沿着地平线路径基本上是无限的即使在晴空。这条道路的照明是阳光的来源。一个大型的光学厚度积雨云本质上也是无限的,照明也阳光的来源。然而,最亮的光芒积雨云较大,大约四倍,比清晰的地平线的天空。这是显示在图8.6中,测量光谱辐射的比值的氧化镁粉,模拟一个厚厚的云,被日光(即。的光辉,阳光直射和天窗)地平线。
尽管情商。(8.12)是严格有效的只有小«1)正常的光学厚度,它确实表明随着光学厚度梯度(角)的天窗光辉应该减少。事实上,这就是观察:天空是阴暗的天更近均匀明亮。此外,Eq。(8.12)在大气中也表明,作为一个提升,因此rn上面所有的海拔降低,天窗应该增加的梯度;这可以从飞机上观察到。
它遵循从情商的情节。(8.1)在图5.13和蓝天的分子光谱光学厚度并非不可避免。光学厚度小于2.2,天窗辐照度相对于太阳辐照度随光学厚度增加而增大。因为分子大气光学厚度的增加与减少波长在可见光谱小于0.36(图8.2),天窗辐照度增加而减小波长。但对于光学厚度大于2.2,天窗辐照度随光学厚度增加而减小。可见最小的分子光学厚度约为0.04(700海里)。因此如果大气厚约50倍天窗辐照度会降低减少波长。图8.7显示了计算光谱天顶黑色地面上空的大气分子与当前正常的光学厚度以及假设大气10厚和40倍。我们需要避免的是意外:如果地球大气层厚得多天空不仅会亮,它的颜色会与现在有很大不同。
通过展示,蓝天不是不可避免的,我们希望给你认为不可想象的。我们强调,白色地平线的天空不是“大颗粒”的结果,而是出现在一个纯粹的分子的气氛。现在,我们要把这个在其头部和断言,“大颗粒”不仅没有必要白地平线的天空,他们可以使它更蓝了。
方程(8.3)的空气光具有相同形式的大气分子和粒子填充,因为散射系数和光学厚度是附加的。足够大的总光学厚度沿着地平线,地平线光辉
p是分子的加权平均相位函数()和粒子(p):
了解方程式的可观察到的后果。(8.13)和(8.14)考虑一些极限情况。假设两个散射向观察者和总散射是由粒子(ftppp > / 3 mpm和/ 3 p > 3米):
如果颗粒大,角散射是独立的波长散射角度感兴趣的tf,空中光频谱是白色的(即。源L0)。这里没有惊喜。
现在假设散射向观察者和总散射是由分子(3 mpm > 3购买力平价和3 m > 3 p):
源的光辉,因为分子阶段功能是好的近似独立的波长。方程(8.14)还预测一个白色的地平线如果足够小的粒子散射的分子散射波长的依赖一样。
如果分子占据总散射而主导散射粒子向观察者(3 m > 3 p和ppp > 3 mpm)
这里地平线光辉逆相关分子散射系数,因此空气光是红色的。这是一个变化的主题上遥远的红色云下一部分要讨论的颜色在日出日落。粒子分布在整个视线扮演相同的角色,本地化的云。
的交谈当我们考虑前面的极限情况,即总散射由粒子但散射向观察者由分子(3 p > 3 m和3 mpm > 3 ppp),我们获得一个令人惊讶的结果:
对于这个示例,地平线空气光是蓝色的。要理解这一点也许contra-intuitive结果我们回到纯粹的大气分子的例子,地平线的天空是白色的,即使选择性散射。散射的阳光向观察者倾向于短的光波长的可见光谱。如果这光传播没有衰减,空中光将蓝色。但不可能分子散射光线向观察者也没有散射的光的视线。这种选择性衰减的光分散向观察者倾向于长波长的光谱。足够长光程选择性散射向观察者正是平衡选择性散射出视线。
现在我们可以更好地理解为什么大颗粒,与预期的相反,使比它原本是地平线的天空更蓝。鉴于假设潜在的Eq。(8.18)我们可以把空气光光辉
因子3 mpm wavelength-dependent散射向观察者和沿着视线到处都是相同的。是一个衰减函数的积分;积分的指数项的概率是光散射x向观察者不会分散在遍历这个距离。虽然光散落在视线上的所有点有助于光辉,大部分的贡献来自于散射在距离小于3 / (3 m + 3 p),这大约是3/3P如果3 p > 3 m。然而,在这样的距离,分子散射不大大脸红了透射光(即。1,exp {3 mx}«x < 3/3p)。因此,色彩平衡不是由衰减恢复,因为它是一个纯粹的分子的气氛。
在他的著名的书光的本质和颜色在露天,Marcel Minnaert指出,“这一天有科学家并不认为蓝色的天空是明确解决的问题……发生在非常特殊的日子里,也许甚至一年一次,天空是漂亮的蓝色到地平线。仔细观察这些天应该记录和描述……根据散射理论,这种现象是不可能的:等层厚度,空气应该出现白色的。”Yet the "theory of scattering" [Eq. (8.18)] does show why the sky can be beautifully blue right down to the horizon, although Minnaert was correct in saying that this is "exceptional." The concentration of particles has to be high enough that total scattering is dominated by them, but sufficiently low that differential scattering is dominated by molecules. This is possible
继续阅读:大气的视觉范围
这篇文章有用吗?