ITCZ季风爆发的突然纬向运动

的热带辐合带(ITCZ)是地面风汇聚并上升到哈德利/的向上分支的位置吗沃克环流．潜在的释放热量在ITCZ中驱动Hadley/Walker循环。换句话说，ITCZ是Hadley/Walker循环的一部分。ITCZ的纬度位置和强度影响热带地面风的分布，进而影响海气相互作用。后者在厄尔尼诺现象中起着至关重要的作用。印度洋和西太平洋ITCZ内的对流存在季节内振荡，称为MJO振荡。当ITCZ在赤道上方时MJO最强。因此，ITCZ纬向移动的年周期决定了MJO强度的季节变化。

由于ITCZ的重要性，它的纬度位置吸引了许多著名研究者的注意，如Charney(1971)。查尼关于ITCZ的纬度位置的理论是建立在他的CISK理论(第二类条件不稳定性;查尼和埃利亚森，1964年;和Ooyama 1964)，他用它来解释热带气旋的成因。Chaney的ITCZ理论是CISK理论的纬向平均版本。根据CISK，天气尺度对流依赖于摩擦诱导的边界层辐合(即埃克曼泵浦)，因此有利于高纬度，即两极。查尼还提出了赤道热带地区的水分供应比极地地区高的观点。这两个因素的折衷使ITCZ在纬度上的位置接近赤道，但不在赤道。

查尼ITCZ理论影响很大。许多人采用或美化它(见Chao and Chen, 2004的附录)。然而，Charney的ITCZ理论及其分支被证明与Sumi(1991)、Kirtman和Schneider(1996)、Chao(2000)和Chao和Chen (2001a, 2004)的水行星(AP)实验相冲突。这些研究人员使用了具有均匀海面温度(SST)的AP模型太阳角-这消除了查尼理论中的第二个因素-并获得了赤道上方或赤道附近的ITCZ(约在北纬14°或南纬14°)，而不是极地上方的ITCZ，正如查尼ITCZ理论的第一个因素所预测的那样。c与我们的主题相关的是，赤道附近的区域(例如从4°到8°)不能或很少能被AP ITCZ所接近，这清楚地表明了多重平衡。

charney在他生命的最后几年意识到CISK理论的问题。荒川个人交流)。

以下是作者对AP模型结果的解释(来自Chao和Chen, 2004)。如果将地球自转速率Q设为零，那么具有均匀海表温度和太阳角度的AP模型将具有均匀的时间平均降水，因为在没有Q的情况下，地球上的一个位置与另一个位置是无法区分的。当使用地球的真实自转速率时，对流会找到首选的纬度。为了解释这些首选纬度，人们应该看看对流的原因，即在科里奥利参数存在的情况下，垂直不稳定性变为负值;换句话说，惯性重力波的平方频率，w2 = f2 + a2 n2 + |，变成负数，并且对流发生[Gill, 1982年Eq.(8.4.23)]。其中，N2为垂直稳定性，|f |为摩擦稳定性，a为波单元或对流单元的垂直尺度与水平尺度之比。在w2的定义中，f2被添加到与N2成比例的项中，这表明f2对对流的影响与N2相当;对于这种等价性的解释，请参见Chao和Chen (2001a)。当a很大时，就像水平尺度较小的单个云的情况一样，f2可以忽略。然而，当我们考虑ITCZ的天气尺度对流系统时，f2是不可忽略的。f对N的等价性使得赤道成为ITCZ的吸引子。因此，当N2在全球均匀时，w2在赤道处是最小值。这意味着对流，或ITCZ，应该发生在赤道-这是f对ITCZ的第一效应。在AP模型中，考虑到辐射冷却和地表的不稳定效应，对流必然发生在某处感潜热通量。对流，或更一般的ITCZ，发生在大气最不稳定的纬度，即dw2/d$ = 0，其中$是纬度。这意味着如果忽略|f |， ITCZ发生在-df2 /d$被d(a2 N2)/d$平衡的纬度。N2因边界层蒸发而减少，边界层中的切向风分量增强了边界层蒸发，而切向风分量又是由科里奥利参数(f的第二个效应)诱导的。因此极点是ITCZ的额外吸引子。

d(a2N2)/d$为f修正的地表风-蒸发反馈机制的纬度梯度(a2的作用尚待探讨)。不幸的是，得到d(a2N2)/d$的解析表达式仍然是一个非常困难的挑战，如果不是不可能的话。对于单个云的稳定性，N2等于gdln0/dz，其中0是潜在温度(或饱和大气的等效潜在温度);但对于天气尺度的云系统(或在gcm中，单个云不被模拟，积云参数化被用来表示云的集合)，N2应该是积云集合的垂直稳定性，而不是单个云的垂直稳定性。因此，N2没有已知的简单易处理的解析表达式。因此，我们必须寻求其他手段来推进调查，这一点我们将很快讨论。

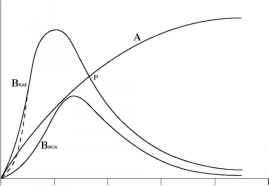
梯度df2/d$可以识别为赤道上ITCZ吸引子的强迫，d(a2N2)/d$可以识别为两极上其他吸引子的强迫。前者的梯度等于8Q2 sin$ cos$，用图5(A)中的曲线A表示;后一个梯度用图5(a)中的曲线B表示。在图中横坐标S是ITCZ的纬度。由于A曲线有已知的解析形式，不依赖于模型设计，因此很容易理解。然而，曲线B没有已知的解析形式;通过数值实验结果和理论论证，构建了该模型。曲线B取决于N2受模型设计影响的方式，特别是受模型物理设计影响的方式。由于曲线B表示对对流系统的吸引力，由于吸引子在极点通过f的第二个效应，它是零在极点-吸引子的中心。同样，曲线B依赖于f的梯度，记住它是a2n2的梯度，a2n2受f的影响，换句话说，曲线B依赖于[。 This gives Curve B a maximum at the equator. However, since the convective system is fairly sizeable,

情商30°N

图5(一个)。示意图显示作用在ITCZ上的两种类型的吸引力的强度。实心曲线和虚线曲线之间的区别在于它们在赤道的斜率。

当它的中心接近赤道时，系统的一部分在另一个半球;因此，它也受到另一极的吸引。因此，曲线B必须在赤道处为零，在那里，由于两极的吸引力相互抵消。如图5(b)所示，虚线曲线是由于f的二次效应而产生的吸引力，如果不考虑对流系统的大小。实心曲线，曲线B -是虚线曲线的运行平均值，具有热带天气系统大小的平均窗口-表示对流系统所经历的净吸引力。

曲线B对积云格式的依赖关系如图5(a)所示。Bras和Bmca分别代表采用宽松Arakawa和Schubert方案(RAS, Moorthi和Suarez, 1992)和Manabe湿润对流调节(MCA)方案时的曲线B。关于BRAS和Bmca的相对高度，首先让我们回顾一下曲线B表示f修正的地表热通量的纬度梯度。当f较大时，向天气尺度对流系统(ITCZ的组成部分)中心聚集的地面风形成较大的切向风分量，风速增大，从而增强了地表热通量。用MCA模拟的对流单元通常比用RAS模拟的对流单元要小，而且朝向对流系统中心的地面风速更快，这使得地面风没有足够的时间被科里奥利参数完全修正，从而使切向风分量完全发展。因此MCA下的曲线B小于

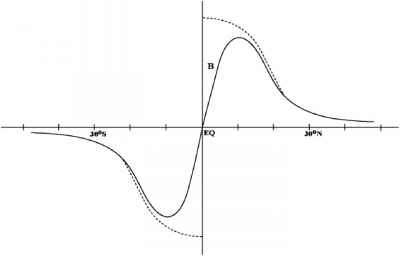
图5 (b)。示意图显示曲线B(实线)作为向两极吸引的大小的纬度运行平均值。

在RAS框架下。有关更详细的讨论，请参阅Chao和Chen(2004)。如果对RAS积云参数化方案施加条件，即边界层相对湿度必须超过临界值才能使方案运行，则该临界值由90%增加到95%，曲线B由Bras变为Bmca。在90%时，标准没有对RAS施加太多限制，但在95%时，限制足够强，使RAS表现得更像MCA。MCA要求模型的两个相邻层都饱和才能运行，因此具有相当的限制性。在图5(a)中，当曲线B从Bmca上升到Bras时，曲线a与曲线B的截距位置，即ITCZ的位置，一直保持在赤道上，直到曲线B在赤道处的斜率超过曲线a在赤道处的斜率。然后赤道不再是一个稳定的平衡位置，ITCZ跳向另一个截距p的纬度，这个跳得非常快，因为ITCZ被两条曲线之间的巨大差异拉成“自由落体”。另一方面，当曲线B从Bras下降到Bmca时，点P即ITCZ逐渐向赤道移动，直到曲线B的峰值低于曲线a，此时P消失，状态向赤道跳跃。但是，在这种情况下，两条曲线之间的差异比ITCZ从赤道跳开的情况要小得多，后者涉及到一个上升的曲线b，因此，ITCZ回到赤道的运动不是那么突然。

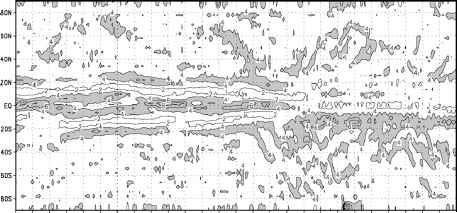
以上推论在图6(a)所示的实验中得到验证，前200天边界层相对湿度判据保持在90%，在接下来的100天，边界层相对湿度判据随时间线性变化至95%，然后保持不变以提醒实验。如图6(a)所示，实验开始时ITCZ远离赤道，然后随着RH判据的增大逐渐向赤道移动。在实验的第一阶段，模拟的ITCZ相对于赤道是不对称的，这一事实仍有待解释。图6(b)显示了一个相同实验的结果，只是90%和95%的值互换了。在这个实验中，远离赤道的移动是突然的，具有大灾难的特征。同样，在另一个实验中

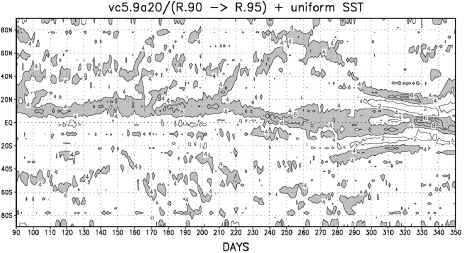
图6 (a)。利用RAS在全球和时间均匀海温(29°C)和太阳角的AP实验中的纬向平均降水速率(mm/day)。临界边界层湿度在前200天设置为90%，在接下来的100天线性变化为95%。

继续阅读:米

这篇文章有用吗?

0 0