平衡常数
本附录主要供参考。在作了一些说明之后,列出了各种化学计量平衡常数的表达式。这些平衡常数是温度、压力和盐度的函数,通过拟合实验数据得到。使用一组一致的平衡常数是绝对必要的。使用的常数应从相同介质(即天然或人工海水)的测量中得出,并转换为相同的浓度单位和相同的pH值。DOE(1994)中总结的平衡常数(人工海水,浓度单位为mol (kg-soln)-1;total pH-scale = pHT)是推荐的(见下面的讨论)。包含平衡常数的MATLAB文件(equic.m)可在我们的网页上获得:http://www.awi-bremerhaven.de/Carbon/co2book.htmr。
在列出各种平衡常数之前,先作几点说明。平衡常数的经验公式通常适用于表面压力(1atm),并经常限制在一定的温度和盐度范围内(详细信息见原始论文);因此,不要推断出S = 0(淡水)!Millero(1995)总结的计算压力对平衡常数影响的方程载于a . all节。
推荐浓度单位为mol (kg-solution)-1(短mol (kg-soln)-1或更短mol kg-1),如DOE(1994)。使用重量单位如mol (kg-soln)-1可得到与温度和压力无关的DIC和TA值。如果没有特别说明,则使用此单位。其他浓度单位(不推荐)是mol l-1(摩尔浓度)和mol (kg-H20) ^molality1)。mol 11(摩尔浓度)、mol (kg-H20)_1(摩尔浓度)和mol (kg-soln)之间的换算1 (Millero, 1995)是:
= In K*[mol (kg-H20)"1] + ln(l - 0.001005 S) (A.0.1)
K ?[mol l"1] = K*[mol (kg-soln)"1]•Psw(T,^g m~3] (A.0.2)
其中psw(T, 5)是海水密度(例如,见UNESCO(1983)或Gill(1982))。
我们还将简要讨论数学方程中使用的量的量纲(或单位)。一般来说,必须认识到两种不同类型的方程:量纲正确的方程和量纲错误的方程。方程优先以量纲正确的形式表述,即方程的形式不依赖于所使用的单位,只要相同的单位适用于方程的所有项。例如,牛顿著名的方程,将质量为m的物体的加速度a与所施加的力的和F^联系起来。
I在尺寸上是正确的,因此无论长度是用米、厘米、英尺还是码来测量都无关紧要。在量纲正确的表达式中,指数函数或对数函数的参数是无量纲的。在Arrhenius方程(Eq. 2.2.7)中就是这样:
EJRT是无量纲的,Ea和RT可以以J摩尔-1或cal摩尔-1为单位给出。在有几个相加项的方程中,如式(A.0.3),每个和必须具有相同的维数。这个性质可以用来发现给定方程中的不一致性。然而,尽管量纲正确方程具有这种优势,但第二种一般类型的方程,即量纲错误方程被广泛使用(顺便说一下,本书在这方面也不例外)。这种类型的方程只有在应用特定的单位时才会给出正确的值。这些单位必须明确地与公式一起提供,或者必须为社区所熟知(普遍接受的惯例)。
本附录中给出的平衡常数A'*的表达式在量纲上是不正确的。例如,它们产生正确的值
实验室实验中常用质量摩尔浓度代替摩尔浓度。
只有当K*以mol (kg-soln)-1为单位,K^以mol2 (kg-soln)-2为单位,T以K为单位(一个普遍接受的惯例),以此类推。相反,当K*为//mol I-1, T为°C时,它们会产生不正确的值。另一个维度错误表达式的例子是pH值的定义:
这个表达式只有在使用[H+]的特定单位(mol (kg-soln)-1)时才有意义。jjH表达式可以按照p\\:= -log([H+]/n,其中k°= 1 mol (kg-soln)-1进行修正。例如,这种方法在DOE(1994)中用于平衡常数的经验表达式。然而,我们将在本附录中明确地写出平衡常数的单位。
A.l co2:酸度常数K\和
碳酸的第一和第二酸度常数K{:= [H+][HC0J]/[C02]
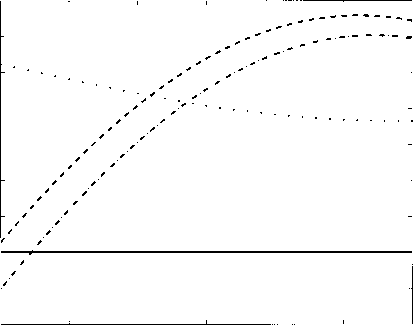
由Mehrbach et al. (1973), Hansson (1973b)确定(原始数据由Dickson和Millero(1987)改装;这些修正将被称为“Mehrbach”和“Hansson”常数),Goyet和Poisson(1989)和Roy等人(1993a)。Mehrbach等人(1973)使用天然海水,而其他所有工作人员都使用人工海水。对于不同的参数,不同的常数集似乎做得更好(参见第1.1.6节的讨论)。例如Wanninkhof et al. (1999), Johnson et al. (1999), Lee et al.(2000)。和Lueker等人(2000)证明Mehrbach常数在从DIC和TA中确定二氧化碳/ co2的分压(更准确地说逸度)时产生了更好的一致性(图A.1.1)。这三个参数的组合是非常重要的,因为它被用于全球碳循环模型。这些模型包含DIC和TA的预后方程,从中计算/C02。这反过来又决定了气体与大气的交换取决于
395 390 385 380
O 370 O
365 360 355 350
0 5 10 15 20 25 30
温度(°C)
利用不同作者给出的酸度常数(pK*和pK~2),从DIC和TA中得到。DIC (T)由TA = 2300 /¿mol kg-1和/C02 = 360 /iatm计算,使用“Mehrbach”常数。然后,利用“汉森”常数(虚线)、Goyet和Poisson (1989;虚线)和DOE (1994;虚线)。差异可达30 /tatm,并取决于温度。比较Wanninkhof et al. (1999), Johnson et al.(1999)和Lee et al.(2000)进行进一步讨论。
关于水和空气的分压差。因此,推荐使用Mehrbach常数,而不是DOE(1994)中总结的Roy常数。值得注意的是,当考虑在海洋中(即在天然海水中)进行测量时,梅尔巴赫常数可能会做得很好,因为这些常数已经在天然海水中确定了。
目前,从天然海水测量中得到的所有相关平衡常数(A'j, A'2, A'^,, A'g, A'p, A'g,…)都没有一致的集合。由于我们必须在本书中计算碳酸盐系统参数的各种组合,所以我们使用了DOE(1994)提供的基于人工海洋测量的一致常数集
水。这组常量在本附录中被称为“推荐的”。
推荐:DOE (1994)
根据Roy et al. (1993a)人工海水,pHT, mol (kg-soln)-1:
In ii J = 2.83655 - 2307.1266/T- 1.5529413 In T- (0.207608410 + 4.0484/T) y/S +0.0846834 5 - 0.00654208 S3/2 + ln(l - 0.001005 S)
检查值:在A'* = -13.4847, pK\ = 5.8563 at 5 = 35, Tc = 25°C。
In K* = -9.226508 - 3351.6106/T - 0.2005743 In T -(0.106901773 + 23.9722/T) VS +0.1130822 S - 0.00846934 S3/2 + ln(l - 0.001005 S)
检查值:K* = -20.5504。pK* = 8.9249 at S = 35, Tc = 25°C。“Mehrbach”
'Mehrbach' = Mehrbach等人(1973)的数据(天然海水),经Dickson和Millero(1987)改装;pHsws, mol (kg-soln)-1:
pK* = 3670.7/T- 62.008 + 9.7944 lnT - 0.0118 S + 0.000116 S2 pIC2 = 1394.7/T + 4.777 - 0.0184 S + 0.000118 S2。
检测值:pK* = 5.8372, pK* = 8.9554,温度S = 35, Tc = 25°C。
Mehrbach常数也由Lueker等人在总尺度上给出(2000);pHx, mol (kg-soln)-1:
pA"* = 3633.86/T - 61.2172 + 9.6777 In T - 0.011555 S + 0.0001152 S2 pK* = 471.78/T+ 25.9290 - 3.16967 lnT - 0.01781 S + 0.0001122 S2检测值:pK* = 5.8472和pK* = 8.9660 at S = 35, Tc = 25°C。
“汉森”
“Hansson”=由Dickson和Millero(1987)改装的Hansson (1973b)数据(人工海水);pHsws, mol (kg-soln)-1:
piq = 851.4/T + 3.237 - 0.0106 5 + 0.000105 S2
pK2 = -3885.4/r + 125.844 - 18.141 In T - 0.0192 5* + 0.000132 S2。
戈耶和泊松(1989)
人工海水(含氟),pHsws, mol (kg-soln)- 1,10 < S < 50, -1°C pKl = 807.18/T + 3.374 - 0.00175 S在T + 0.000095 S2, pK* = 1486.6/T + 4.491 - 0.00412 S In T + 0.000215 S2 (请注意,这些是Goyet和Poisson(1989)表4中给出的方程,而摘要中的方程来自包括Hansson (1973b)结果的组合数据集)。 A.2真碳酸的酸度常数 MH2co3 = 3-8 ~ 3-4 举例:[HCO3] = 2 mmol kg"1, [H+] = 10"8 mol (kg-soln)1, K^C03 = 10-3.8 mol kg-i(推荐值)[H2C03] = 1.3•10~7 mol (kg-soln)-1或小于C02浓度的1%。 A.3 CO2在水中的溶解度(亨利定律) 在平衡状态下,二氧化碳浓度与逸度成正比(亨利定律)。 [c02] = k0■/ c02 (a.3.6) 其中K0是亨利常数。单位:[C02] in mol (kg-soln)-1, /C02 in atm, K0 in mol (kg-soln)-1 atm-1。 图a .1.2: Roy et al.(1993)测定并在DOE(1994)中总结的碳酸第一和第二酸度常数作为温度和盐度的函数S = 35:(a) pK*, (b) pl\ *■(c)各pK*相对于DOE的差异(1994):'Mehrbach'(实线),"Hansson'(虚线),Goyet and Poisson(1989)(虚线),(d)各pK*相对于DOE的差异(1994):'Mehrbach'(实线),'Hansson'(虚线),arid Govet and Poisson(1989)(虚线)。 推荐:韦斯(1974) In A0 = 9345.17/7' - 60.2409 + 23.3585 In (T/100) 0.023517 - 0.00023656 t + 0.0047036 (t /100 检查值:K0 = -3.5617, pK0 = 1.5468 at S = 35, Tc = 25°C。 A.4水的离子积:Ii^ 反应的平衡常数k为H20 ^ H+ + OH" 称为水的离子积。 推荐:DOE (1994) +[118.67/r- 5.977 + 1.0495lnT]51/2 - 0.01615 K'w in mol2 (kg-soln)-2;pH-scale: pHT。 检查值:在A'{v = -30.434, pK^ = 13.2173 at 5 = 35, Tc = 25°C。 盐度 图a .4.4: Tc = 25°C时,水的离子积pA'w随盐度的函数 Millero (1995) pHsws, mol2 (kg-soln)“2 +(118.67/T- 5.977+ 1.0495 In T) S1/2 - 0.01615 DOE(1994)和Millero(1995)之间的恒定偏移(148.96502-148.9802 = -0.01518)是pH尺度差异的结果。 A.5硫酸氢钠离子 平衡态HS04- h++ SO2的常数,即[HS04- lnA'g = -4276.1/T + 141.328 - - 23.093 InT + (-13856 / T + 324.57 - 47.986 InT)/1/2 + (35474 / T - 771.54 + 114.723 In T)/ 2698 r3/2—7Z-I ' + 1776 r2 In (1 - 0.001005 S) T 是离子强度.A'g mol (kg-soln)-1;pH-scale:“免费”scale。检测值:In = -2.2996, pK£= 0.9987在S = 35, Tc = 25°C。总硫酸盐浓度ST是盐度的函数: 圣(摩尔(kg-soln) 1): =[就是HSO4] +[所以^ ~]= 0.02824 ^ (A.5.9) A.6氟化氢 平衡HF h++ F~的常数,即; 由Dickson和Riley(1979)给出(在DOE(1994)中转载): In A'p = 12.641 + 1.525 I1'2 在哪里 是离子强度。 °'50 5 10 15 20 25 30 温度(°C) 图a .5.5: S = 35时硫酸氢的稳定常数pK*随温度的变化。 术语ln(l + ST/K^)从“自由”氢离子浓度尺度转换为“总”(汉森)尺度。 检测值:Ap = -5.7986, pA'£= 2.5183,S = 35, Te= 25°C。海水中总氟浓度FT. er与盐度有关 Fr (inol (kg-soln) 1): =(高频)+ (F ~) = 7•10 ~ 5 ^ (A.6.11) A.7硼酸 平衡的常数 B(0H)3 + H.20 = H+ +B(OH)4,即 _ [h +][b (oh)-] vb ' [b (oh)3] " 是由 推荐:DOE (1994) (根据Dickson, 1990) 在A'b = (-8966.90 - 2890.53 S1^2 - 77.942 S + 1.728 S3^2 -0.0996 S2)± + 148.0248 + 137.1942 S1/2 + 1.62142 5 -(24.4344 + 25.085 S1/2 + 0.2474 S) In T +0.053105 Sl/2T pH-scale: pHT;单位:A'g mol (kg-soln)-1;检查值:A'g = -19.7964, pKg = 8.5975, S = 35, Tc = 25°C。 注:此方程与Rov et, al. (1993b)的测量结果非常吻合。 海水中总硼浓度BT与盐度的关系为BT(mol (kg-soln)"1):= [B(OH)3] + [B(0H)7] (A.7.14) DOE(1994,第5章,p.ll)。如系磷酸 平衡的常数 这篇文章有用吗?






