二氧化碳的水

最后更新2023年1月2日星期一|碳酸盐系统

co2动力学的一个非常重要的特征是水化步骤(从状态(I)过渡到状态(II))是一个“缓慢”的反应。被缓慢的

2根据Stumm和Morgan(1996)， 25°C时[C02]与[H2C03]的比值在350到990之间。因此，真正的H2CO3浓度小于[CO-¿]的0.3%。

我们的意思是这个反应的反应速率比其他一些快得多的反应慢。H2CO:s脱水的速率常数约为104 kg mol-1 s”1，而扩散控制反应(见下)的速率常数约为1010 kg mol-1 s”1。碳酸和碳酸氢盐(II) ^ (III)之间的反应是那种性质的，实际上是瞬时的。因此，可以假设均衡关系成立:

[H+PCO3-] = -^'H2co3 [H2C03]•(2.3.13)

无法确定水化反应是直接发生，即(I) (III)还是通过(I) ->•(II) (III)发生(Eigen et al.， 1961)。唯一可测量的量是对应于整个反应的速率常数(碳酸可以使用式(2.3.13)消除):fc+i

C02 + h20 h + + hcoj (2.3.14)

k+1:= k*+ j + k+2(在文献中通常称为kcGz) (2.3.15)

这些关系可以通过写出式(2.3.12)中三角形反应的速率定律来推导(见练习)。溶剂H20的浓度与溶质的浓度相比是如此之大，以至于可以安全地假设它是恒定的。

在低pR时，C02的水化反应(2.3.14)占优势，而在高pR时，随着0H~离子数量的增加，有利于以下羟基化反应:

(对比图2.3.5)。值得注意的是，C02和HCO7之间的化学平衡(即碳酸的第一解离常数Kj的值)不依赖于反应机理。热力学平衡是由分子的能量给出的(参见第3.5节)，因此不依赖于达到平衡的化学途径。

值得注意的是，C02的水合作用和羟基化作用(等式。(2.3.14)和(2.3.17))是基本反应。由此可见，之间的关系平衡常数速率常数可以写成(cf。

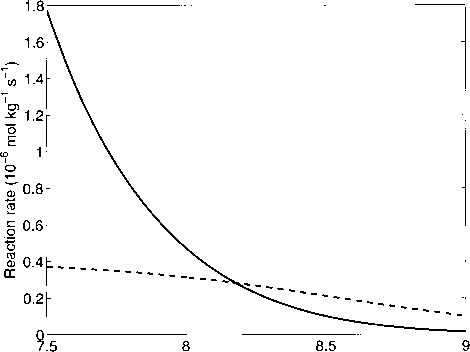
图2.3.5:(2.3.14)和(2.3.17)反应在Tc = 25℃，S = 35, TA = 2300 ftiriol kg-1时的正向反应速率k+1 [C02](实线)和k+i [C02][0H~](虚线)。pH < 8.2时，反应(2.3.14)对COo向HCOr的转化最为重要。随着pH的增加(降低[C02])，其速率比反应(2.3.17)下降更快，在较高pH时占主导地位。

1 " [co2] - r;- r;W (3-18)

其中Kyy = [II+][OH]是水的离子产物。

综上所述，描述co2在水溶液中的水化反应和速率常数的集合为:

有趣的是，这两种反应在典型表面海洋pR为8.2的海水中同样重要，这可以通过考虑反应速率来证明:

~ (4.0 × 103) (1 × 10~5) (1 × 10-5) = 4.0 × 10"7 mol kg"1 s-1

其中采用ec02 = 2 mmol kg-1, pR = 8.2, S = 35, T = 25℃时海水中[c02]和[OH-]的近似值。用于反应速率k+1和k+A的值将在下一节中详细讨论。

2.3.2速率常数k±i和k±4的温度依赖性

图2.3.6显示了在海水中测定的“慢”反应速率常数和k±4)的值及其温度依赖性，而110页的表2.3.1总结了完整的速率常数集的信息。正反应速率常数的值，k+1(图2.3.6a，实线)和k+4(图2.3.6b，虚线)，是从Johnson(1982)的工作中获得的(钻石)。Johnson在5、15、25、35℃条件下，用陈化两个月后过滤的天然海水，测量了co2水化和羟基化反应的速率常数。图2.3.6中还显示了Miller et al.(1971)在人工海水(方格)中确定的值，该值与Johnson的值一致(见下文讨论)。反向反应速率常数k_1的值(图2.3.6b，实

~ (0.037)(1 × 10”5)= 3.7 × 10”7 mol kg”

: 103/ t (k)

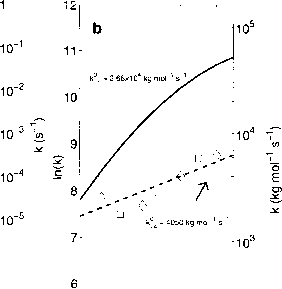
图2.3.6:慢反应的速率常数碳酸盐系统：

C02 + h20k ^ h++ HC07和C02 + OH“HCO”作为温度的函数。

图2.3.6:碳酸盐体系“慢”反应的速率常数:

C02 + h20k ^ h++ HC07和C02 + OH“HCO”作为温度的函数。

(a) k+1和(b)的实验数据来自Johnson(1982)(菱形)和Miller et al.(1971)(方形)。实线(a)和虚线(b)是拟合约翰逊数据的曲线(见正文)。(a，虚线)和k-i (b，实线)的曲线采用平衡常数计算(Eq. 2.3.18);fc®是指速率常数k在25°C时的值。

(图2.3.6a. line)和k_4。虚线)由正向反应速率和平衡常数计算，使用Eq. (2.3.IS)。

正如观察到的一些溶质之间的反应，这里是C02。溶剂是H20。速率常数的温度依赖性显示出偏离简单的“阿累尼乌斯行为”，即，h\{k) vs. 1的曲线显示出相当大的曲率(图2.3.6a)。然后，将数据拟合到如下形式的曲线上是有用的:

C02水化的速率常数A’+1在淡水(cf. Kern, 1960)和海水(Johnson, 1982;米勒等人。1971)。Johnson(1982)确定的、4、B和C的值见表2.3.1。反应的表观活化能。Ea，在这种情况下不是常数，而是温度的函数。它由ln(fc)与l/T的斜率给出，当k+1时，在海水中5°到35°C, ln(fc)与l/T的斜率从Ea = 90下降到45 kJ mol-1。这种表观活化能与淡水的值很一致(在0°和40°C之间，Ea从80下降到45 kJ mol-1, Kern (I960))。

因为只有不带电的物质(C02和H20)参与水化反应，k+1不应该取决于离子强度解的。实际上，Johnson(1982)和Miller等人(1971)都没有分别观察到盐度在3.4 - 37.1和30.7 - 39.7变化时k+1的系统性变化25°C时海水值k+1 = 0.037 s-1与淡水值k+1 = 0.040 s-1几乎相同(Knoche, 1980)。

图2.3.6b(钻石)中k+4的数据来自Johnson(1982)的工作，详见附录C.6。值得注意的是，k+4的数据比k+1的数据显示出更大的离散性。图2.3.6b中的虚线是对Johnson数据的拟合(另见表2.3.1)。使用阿伦尼乌斯方程是因为测量值与简单阿伦尼乌斯行为之间的温度依赖性的偏差似乎是非系统的，因此不支持式(2.3.21)的拟合形式。25°C海水中k+4的值大约比淡水中的值(8500 kg mol-1 s-1, Kern, 1960)小1 / 2，这可能是由于离子强度对速率常数的影响(见下文)。还注意到，由In(k)与l/T的线性回归斜率给出的~20 kJ mol-1的活化能大约比淡水中的活化能小3倍。然而，由于的测量值存在非系统的散射，这种说法不应过于严格。如果从数据集中删除5°C时k+4的测量值，则计算出的斜率将急剧增加。我们的结论是，对海水中二氧化碳羟基化反应的速率常数k+4进行进一步的实验工作是必要的，特别是由于数据的分散以及Miller等人(1971)和Johnson(1982)的结果的差异。没有试图包括盐度对k+4的影响(见表2.3.1)。

离子强度对反应速率的影响

关于离子强度和盐度对反应速率的影响的一个评论似乎是合理的。用过渡态理论可以证明

miller等人(1971)研究了17、19和22%氯度(CI)的溶液，CI被定义为在328.5233 g海水中沉淀卤素(CI-和Br-)所需的银的质量(以克为单位)，并与盐度相关5 = 1.80655 CI。

稀溶液中离子的反应速率可写成(Steinfeld et al.， 1999):

zAzBVl (2 -3.22)

其中k0为无限稀释时的反应速率，zB分别为A离子和B离子的电荷量;I = 1/2 S ctzf是离子强度，其中c是指溶液中所有离子的浓度。结果表明，电荷相似的离子反应速率随离子强度增大而增大，电荷相反的离子反应速率则随离子强度减小而减小。这种行为通常被称为“初级盐效应”，并在许多反应中观察到(另见Moore和Pearson, 1981)。溶液中电荷相似的离子的离子气氛倾向于降低离子之间的静电斥力，从而提高离子之间的碰撞率。另一方面，对于电荷相反的离子，离子大气倾向于降低离子的静电吸引力，因此导致降低碰撞率。

如果其中一个反应物是中性分子，即2 = 0。式(2.3.22)预测离子强度对反应速率没有影响。然而，离子强度对例如海水中C02 + 0H~反应的轻微影响确实被观察到(Johnson, 1982)。在较高的离子强度下，离子活度系数与公式(2.3.22)所基于的Debye-Hiickel理论存在偏差(见1.1.2节)。此外，中性分子的活度系数在较高的离子强度下受到影响。因此，式(2.3.22)不能严格地应用于诸如海水这样的溶液，因为它只适用于非常稀的溶液。

离子强度的增加也可能改变反应机理，因为离子在溶液和矿物表面的相互作用。一个例子是不同离子强度的海水中方解石的沉淀。Zuddas和Mucci(1998)提出离子强度的增加会导致沉淀机制的改变，这可能会显著改变生长中的方解石晶体表面的过程。

2.3.3扩散控制反应的速率常数

如前所述，扩散控制反应的速率常数比co2水化反应的速率常数大得多。扩散控制反应的特征时间尺度或衰减时间通常为微秒级，而C02水化反应的衰减时间为一分钟级。因此，如果考虑的时间尺度比10-b s大得多，可以安全地假设快速反应已经处于平衡状态。然而，考虑到10~6秒的时间尺度，这种近似是无效的。

扩散控制反应的速率限制步骤不是反应机制本身，即化学键的分子重排可能与高活化能有关。相反，是扩散驱动的相遇率限制了反应速率(见103页<相遇率>)。有人可能会说:一旦分子相遇，它们就会发生反应。扩散控制反应的典型活化能为8 - 16 kj mol-1 (Eigen和De Maeyer, 1963)，这导致反应速率对温度的依赖性很小(参见第2.2节)。

已知在水溶液中最快的反应之一是H+和OH的重新结合”:

k + 6
n2°±11+ +油-。	(2.3.23)

在25°C的稀溶液中测量的速率常数k_6为1.4 x 1011 kg mol-1 s-1 (Eigen, 1964)。如果使用淡水值pKyy = 14.01，则k+6的值为1.4 x 10""3 mol kg-1 s_1。H20的离解应该在很大程度上与介质的离子强度无关，因为H20是不带电的。因此，对海水使用淡水值k+6可能是安全的，而海水的k_6可以从以下公式确定:

其在25°C下的值为k_6 - 2.31 X lO10 kg mol-1 s-1(见表2.3.1)。如2.1节所述，这个大的速率常数导致反应速率(r - k X [H+] X [OH-])在典型的表面海水pR = 8.2和25°C下约为6.3 X 10”3 mol kg-1 s_1或OH”的周转时间约为1/630秒。

Diffusion-controlled反应

Eigen和Hammes(1963)写道:“双分子速率常数的最大值是由两个分子扩散在一起的速率决定的。分子a和B之间扩散控制的结合的速率常数可以写成a,s(德拜，1942)

其中NA为阿伏伽德罗数，1)4和DB为A和b的扩散系数，A为它们最接近的距离，IJ为两个分子相互作用的势能。上面的方程是针对球形分子推导出来的。如果反应发生在浓度很低的离子之间，势能V可以写成

)让步

， _ ^NAa(DA + DB){zA~Be20/cakT) exp \ - 1表示离子价电子。E0是电荷，c是介质的介电常数. ...kD值的大致范围为1011 ~ 109 M“1 s”1。

介电常数c由c = ere0给出，其中c0 = 8.8542 X jq-12 p m-i js为真空介电常数，e(。= 80为水在20℃时的相对介电常数;M = mol I-1。

(2.3.23)等快速反应的速率常数可以用电场脉冲法或温度跳变法测量(详见Kigen和De Maeyer(1963))。这些所谓的弛豫方法允许在小于10 //s的时间内有效完成反应的测量。正如已经讨论过的，化学反应的平衡常数取决于系统的温度和压力。例如，在温度跳跃实验中，一个处于平衡状态的系统的温度突然发生变化(在ca. I /.is中可以实现大约5到10 K的温度跳跃)。然后，系统将立即开始根据新的温度调整(或放松)到新的平衡状态，即反应物和生成物的浓度将发生变化。弛豫达到新平衡的速度取决于所涉及的反应的速率常数。因此，在系统弛豫过程中测量反应物和生成物的浓度提供了一种测量快速反应速率常数的方法。Manfred Eigen和他的同事在20世纪50年代和60年代发明了这些强大的技术(cf. Eigen和De Maeyer (1963);特征(1964))。

2.3.4原解和水解

为了完成对碳酸盐体系动力学的描述，我们将讨论碳酸氢盐和碳酸盐以及硼酸和硼酸之间的酸碱平衡:

HCO:

B(oh)3 + h20 ^ B(oh) j + h +。(2.3.28)

一般来说，水溶液中的酸碱平衡可以根据Eigen(1964)给出的通用反应方案来表示。我们将在这里用HCO3和CO2-作为酸及其共轭碱的例子(式(2.3.29))来检验这个方案。

质子迁移

水解

在这个酸碱体系中有两条反应途径达到平衡。第一种路径(I) (III)被称为原水解，在正向反应中酸HCO3解离并提供一个多余的氢离子，或者在反向反应中碱分子CO2-与氢离子结合。第二种途径(II) ^ (III)称为水解，在正向反应中酸HCO3与OH”结合，或在反向反应中碱分子C03~与水分子反应形成缺陷质子。两种反应路径之间的联系是由水(I) ^ (II)的中和和解离提供的。

水解反应的速率常数

Eigen和同事确定为~6 X 109 kg mol-1 s_1

离子强度为1.0(详见Eigen(1964))。假设这个值也适用于海水，并认识到k™= h™X Kyy / A ' 2，则在25°C的海水中ArS ' - ~3 X 105 s-1。我们不知道任何关于原解反应速率的数据

然而，可以有把握地假设，该反应的反应速率与测定的反应速率相似

HCOJ+H+ J7 H. 2co:j (2.3.32)

即= 4.7 X 1010 kg mol-1 s_1，离子强度为0 (cf. Eigen(1964))。同样，假设这个值也适用于海水。使用~5 × 1010千克mol"1 s-1。由= jfc»g X K*可知，在25°C海水中，Ar»* ~ 59 s”1。表2.3.1概述了上一段讨论的反应速率。

值得注意的是，平衡HCO^ - CO3- + II+的平衡时间(是011的10 ' s数量级，见下文)是reacta浓度的函数。nts，因此取决于溶液的pH值。典型地表海水pH值为8.2(总规模。pH = - log [H+])，水解反应(2.3.30)为主要反应，通过比较反应速率可以看出

= (6 × 109) (1.7 × 10”3)(1 × 10~5) ss 100 mol kg“1 s

= (5 × 101U) (3 × 10"1) (6 × 10"9) ss 0.1 mol kg^1 s"1，其中在SC02 = 2 mmol kg-1, s = 35, T = 25°C时，使用海水中[HCO3]和[CO2-]的近似值。

2.3.5硼酸-硼酸盐平衡动力学

在本节中，我们介绍了海水中硼酸-硼酸盐平衡的反应途径和速率常数。迄今为止，硼酸体系的动力学在海洋化学和化学海洋学中尚不清楚。我们从研究海水吸声的物理化学研究中获得了关于这一主题的信息(Mallo等人，1984;Waton等人，1984;详见Zeebe et al.(2001)。

继Mellen等人(1981)和Waton等人(1984)之后，硼酸-硼酸盐平衡的动力学可以用以下反应来描述:

B(oh)3 + oh - B(oh)4-。(2.3.33)

Waton et al.(1984)测定的离子强度I = 0.1时k+7的温度依赖性如图2.3.7a所示。当I在0.1到0.7之间变化时，他们观察到离子强度对k+7的影响很小。因此，Waton等人(1984)报道的k+7值和I = 0.1时的温度依赖性也可能适用于海水(I ~ 0.7)。

用Arrhenius方程拟合得到的数据为1.04 X

107 kg mol-1 s_1在25°C。需要强调的是，与许多其他酸碱平衡相反，反应(2.3.33)不是扩散控制的。速率常数比扩散控制反应的典型速率常数小三到四个数量级。这可能是由于从平面B(OH)3到四面体B(OH)4的转换所涉及的实质性结构变化(参见图3.4.34，第231页)。通过fln(fc+7)与1/T的线性回归计算，该反应的活化能为Ea = 20.8 kJ mol"1。

介绍反应平衡常数(2.3.33):

r* =k±1= [B(OH)4-] iB' k_7 [B(OH)3][OH-] '

利用硼酸的解离常数和水的离子积:

Ab = [B(OH)3] ' Aw - [H][0H]

逆反应速率常数k_7可由以下公式确定:k_7 = ^ = k+7x1{|。(2.3.34)

TfC) 15 25

16.5

15.5

14.5

TfC) 15 25

16.5

15.5

14.5

一个
K°7= 1.04 × 107 kg mof1
+8 a s	✓
“k°=3.26x10®✓-8”	Kg mol-1 s" 1kg mol-1 s"1

1 x10 '

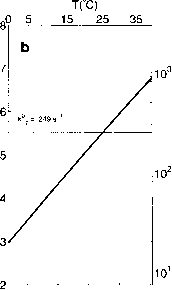
率

硼酸-硼酸盐反应常数随温度的变化:B(OH)j + OH B(OH)4和fc + 8

COl~ + B(OH)3 + H20 ^ B(OH)- + HCO”。(a) k+r和/fc+8的实验数据

都来自笏。on et al.(1984)(钻石)和Mallo et al.(1984)(正方形)。实线已安装在笏。Ons的数据(见正文)。假设k+8(虚线)的温度依赖性与k+7相等。用平衡常数计算k-% (a，虚线)和k-7 (b，实线)的曲线;k°为速率常数kt在25℃时的值。

k_7的温度依赖性如图2.3.7b所示。

在海水中，即在碳酸氢盐和碳酸盐离子存在的情况下，B(OH)3/B(OH);j”和HC03/C03~平衡之间的酸碱交换使情况复杂化。研究表明，碳酸氢盐浓度对硼的弛豫时间有显著影响，表明硼化合物与HC03和C03~离子的相互作用(见Mellen et al.(1981)和Mallo et al.(1984)及其参考文献)。硼酸-硼酸盐与碳酸氢盐-碳酸盐偶联的总体反应可写成:

fc + 8

Co2 " + b (0h)3 + h20 ^ b (0h)-+ hc03。(2.3.35)

值得注意的是，这种机制可能近似于一个更复杂的过程，其中包括中间步骤和一系列耦合反应(比较Mellen等人(1983)和Zeebe等人(2001)的讨论)。

该反应的正向速率常数被确定为k+8 = 1.5 x 107 kg mol“1 s”1，温度为20℃(Mallo et al.， 1984)。为了得到这个值，Mallo等人(1984)用淡水平衡常数拟合了他们的实验数据。利用海水常数，可以在20°C下得到= 6 x 106 kg mol-1 s_1。k+8的温度依赖性(据我们所知)迄今为止还没有研究过。这个反应的活化能很可能与另一个反应的活化能(2.3.33)相似，因为在这两种情况下，速率限制步骤都是硼化合物配位的变化。这一假设与观察到的两种反应在20℃时的速率常数相似是一致的。由此可见，k+8的温度依赖性等于k+7的温度依赖性(图2.3.7，实线和虚线)。

由平衡关系确定后向反应的速率常数。从反应(2.3.35)可以看出:

k + 8 _ [B (0 h) 4 -] [HC03 -] _智商k_8 [B (0 h) 3] [co2 -]的智商:f (*

速率常数k_8作为温度的函数如图2.3.7a(点虚线)所示。

2.3.6总结

碳酸盐岩体系动力学中涉及的反应和速率常数的描述可以概括为:这组反应如下:

B(OH)3 + OH- B(OJI)3 + ll20

K + l丙氨酸

IICO”

生态。”

其速率常数见表2.3.1。练习2.4 (*)

B(OH)，3 + OH ->■B(OH)4反应的活化能约为20 kJ mol

这与扩散控制反应的典型活化能相比如何?

考虑描述主盐效应的式(2.3.22)。画出log A;Vs. (a)带电相似的离子(b)带电相反的离子(检查sa = - 2， - 1， +1， +2和zb = - 2的情况)之间的反应的斜率(大约)是多少。-1， +1， +2)?

CO2和HCO.7之间的平衡是由反应(2.3.14)和(2.3.17)介导的。计算两种反应速率相等时的pH值:Tc = 25°C, S = 30,35和40。

推导方程式。(2.3.11)到(2.3.16)(记下式(2.3.12)中三角形反应中二氧化碳的速率定律)。

率

价值

làaplence在t.s.

讲话

常数在Tc é 2°C, S =5 3

k + 1

0.037 s - 1

lnfc+1lâ46 .98 - 6.19 x 104/T -183.01n(T)

约翰逊(1982)

2.66 × 104 kg mol-1 s-1

k_x = k+1(T)/KÏ(T,S)

计算

k + 4

4.05 × 103 kg mol-1 s-1

k+4 = A4cxV(-EJRT) a

源自约翰逊(1982)

k_ 4

1.76 x IO-4 s

k_4 = k+4(T) xk ^(T,S)/iq(T,S)

计算

LH +

5.0 x 1010千克摩尔“1秒

常数

Eigen(1964)，见正文

59.4 s”1

k”;= k * txiq (T, s)

计算

I.OH”

6.0 × 109 kg mol“1 s

常数

特征(1964)

3.06 x 105 s

k°f~ = x iqv(T,S)/iq(T, S)

计算

1.40 x 10“3 nk$ s

常数

特征(1964)

k_6

2.31 × 1010 kg mol“1 s

k_6 = k+6/ k ^(T,S)

计算

k + 7

1.04 × 107 kg mol"1 s-1

k+7 = A7exp(-E7/RT) a

源自Waton等人(1984)

k_7

249年代“1

k_7 = k+7xK^(T,S)/ k ^T,S)

计算

k + 8

6.92 × 106 kg mol“1 s

k+8 = A8exp(-E8/RT) a

Afteraflfc等人(1984)

k_ 8

3.26 x 106 kg mol-1 s

k_8 = k+sxiq(T,S)/ k *B(T,S)

计算

米

= 4.70 × 107 kg mol"1 s-1;A7 = 4.58 x ÎO10 kg mol"1 s-1;= 3.05 × 1010 kg mol"

1 s - 1;

4 =£

23.2 kJ mol"1;Kr = Es = 20.8 kJ mol"

－1

CD P

年代年代”

阿伊尔

Pj米

Co ni

O费尔

“e

S”

2.4接近平衡:碳酸盐体系

对反应动力学的数学分析的介绍和前面所给出的碳酸盐体系的速率常数的总结，为理解碳酸盐体系的不平衡性质奠定了良好的基础。本节描述了碳酸盐体系对扰动的响应和趋于平衡的弛缓过程，包括碳同位素12C、13C和14C的讨论;氧同位素见3.3.6节。值得注意的是，与已经详细研究过的碳酸盐体系的平衡行为相比(参见第1章)，碳酸盐体系的动力学性质迄今为止受到的关注较少。Lehman(1978)和Usdowski(1982)计算了二氧化碳体系建立化学平衡所需的时间。然而，他们的结果仅限于一个简化的模型，该模型假设CO2的质子化是瞬时平衡的，而H20的平衡是瞬时平衡的。使用这种近似，不能充分描述小于秒的时间尺度。此外，这两种分析都不包括硼化合物，Usdowski(1982)的工作认为硼化合物是一种化学成分淡水系统．

为了描述海水中碳酸盐体系的不平衡性质，我们使用第2.3节中给出的动力学速率常数集(参见Wolf-Gladrow和Riebesell(1997)和Zeebe等人(1999b))。这种方法使我们能够在从微秒到分钟的时间尺度上分析系统。所得结果可用于。例如，在海洋硅藻中鉴定无机碳源(同位素不平衡技术，参见Korb等人(1997))或在测量初级产量时确定同位素平衡时间。

值得注意的是，下面考虑的是一个封闭的海水系统。换句话说，为化学和同位素平衡计算的弛豫时间指的是一个不允许质量迁移或气体交换的系统。开放系统的松弛时间可能与封闭系统的松弛时间有很大的不同，特别是当涉及到同位素时(例如Broecker arid Peng, 1974;Lynch-Stieglitz等人，1995)。

2.4.1 co2的平衡时间

如第2.3.1节所述，碳酸盐体系弛豫最慢的过程是二氧化碳和其他化学物质之间的平衡

: 图2.4.8:CO2中扰动的松弛。r秒后，扰动降低到初始值(6C02°)的~ 37%。

物种。因为H+和0H~和碳酸氢盐-的重组碳酸盐平衡是非常快的，可以假设这些反应在C02平衡的时间尺度上处于平衡状态。在本节中，描述了长1 s时间尺度上碳酸盐岩系统的动力学，而所有时间尺度(包括/is)在第2.4.2节中讨论。

在下文中，使用2.1节中介绍的松弛时间r来表征系统的时间行为。在这种情况下，r指的是扰动达到其初值约37% 1 /e)的时间。例如，在更长~1秒的时间尺度上，C02(=¿C02)中扰动的速率定律可以写成(见附录C.7):

这个方程与放射性衰变方程的形式相同，其中衰变率dN/dt(每次衰变的数量)与原子数量(N)成正比:diV/di = -AN。因为相同的方程有相同的解，所以解是指数函数:

¿C02 = 6C02°exp (-t/r) (2.4.44)

其中¿C02°是t = 0时对C02的扰动。换句话说，co2中的扰动呈指数下降，r秒后达到初始值的~ 37%(图2.4.8)。

C02平衡时间随pH值变化的计算公式见附录C.7。该公式只适用于H+/OH~的酸碱平衡大于1 s的时间尺度

图2.4.9:封闭海水体系(T = 25°C, S = 35)中CO2平衡的弛豫时间r。数字表示不同的ECO2值。请注意，SC02的小值并不是海水中ECO2的典型值——这里包括这些值是因为这些值在讨论碳同位素14c和13c时很有用(见第2.5节)。

HCO7/CO3-已经建立(关于这些过程的动力学，参见第2.4.2节)。除了C02的水化作用外，hvdrox的化合作用也被考虑在内。根据式(C.7.25)， C02平衡的弛缓时间在图2.4.9中显示为pR的函数。在高pR时，高浓度的OH-导致了小的平衡时间(羟基化/去羟基化)，而在低pR时，高浓度的H+加速了平衡(水化/脱水)。在中等pH值下，反应物浓度相似，弛豫时间最大。对于典型的海面海水条件，即pR = 8.2, SC02 = 2 × 10-3 mol kg-1，弛缓时间为13.5 s。

总溶解无机碳基化合物XC02的浓度对弛豫时间的影响也如图2.4.9所示。较高的SC02值导致略小的松弛时间。对于小浓度的XC02(£10”7 mol kg-1)，弛缓时间可以近似为:

- = (*+!+ [H+r + k_4 + k+4 [OH-]*)。(2.4.45)

例如，在pR - 7, T = 25°C, S = 35时，我们有T = (0.037+(2.66 x 104)(10"7) + 1.76 x 10"4

+ (4.05 × 103)(10-13'22)/(10-7) _1 = 23.7 s。

天然海水经每公斤添加1 mg NaHCC>3处理。(大约)需要多长时间才能建立化学平衡(T = 25°C, 5 = 35)?给出一个r值(~63%平衡)和一个值为99%平衡。

为什么CO2平衡的弛豫时间(式(C.7.25))与CO2的浓度无关碳酸盐物种UC02低?

2.4.2完整的化学体系

在本节中，考虑了与碳酸盐体系弛豫有关的所有时间尺度。这些时间刻度范围从ps到minutes。完整的化学体系(包括硼)由第109页(2.3.36)-(2.3.42)的反应给出。所考虑的反应的总溶解碳、碱度和总溶解硼的定义为:

£c02 = [c02] + [hco3] + [co2 "]

TA = (HC03) + 2 (co2 -] + [B (0 H) 4] + [0 H”]- [H +] Bt = [B (OH) 3] + [B (OII) 4 -]。

请注意，PO4-和SiO(OH)g等物种对总碱度的微小贡献被忽略了。完整碳酸盐体系相应的动力学速率规律见附录C.8。

使用动力系统理论对系统进行数学分析(见例如Zeebe等人(1999b))产生了4个特征时间尺度

图2.4.10:CO2扰动导致的碳酸盐物种松弛(线性系统)(CO2-在t = 0时减少6CO2，以保持ECO2恒定，而OH-增加2 6CO2，以保持碱度恒定，另见图2.4.11)。包括硼在内的所有化学物质都被考虑在内。虚线表示各物种的平衡值，由SC02 = 2000 /imol kg"1和TA = 2437 /irnol kg"1计算(T = 25°C, 5 = 35)。

这个系统。这些时间尺度与以下平衡有关(1)C02 + H20 ^ HCO3 +H+ (2) HCO3 ^ C03~ +H+ (3) H20 ^ H+ + OH”和(4)B(OH)3 + 1120 = BiOH)”H+(见表2.4.2)。值得注意的是，所有的动力学途径，即反应(2.3.36)-(2.3.42)，都涉及到趋于平衡的弛缓过程。数学分析——这里不作详细说明——产生了化合物的时间发展。结果显示在图2.4.10和2.4.11中。

从pH 8.2和[C02] = 7.6¿umol kg-1的平衡开始，在t = 0时，C02增加了1 /imol kg"1。此外，在t = 0时，CO3-和OH”分别减少和增加6C02和2¿C02，以保持SC02和碱度恒定。结果，HCO3、CO2-和pH值在不到一微秒的时间内对这种扰动作出反应。

图2.4.11:同样如图2.4.10对数时间轴,(a)二氧化碳减少10年代的时间尺度。(b) HCO ^”和(c)二氧化碳——先是减少和增加,分别在10 - 7 s结果的时间尺度,然后对硼酸,硼酸平衡时间尺度的身手,尤其最后放松时间尺度上的均衡价值10年代。(d)重组以来哦-和H +是一个快速的过程(10 ~ 7 s)展品pH值变化对所有的时间尺度。(d)中的垂直虚线表示不同的时间尺度(10~7秒、10-4秒和10秒)。

在~ 10-4秒的时间尺度上，除C02外，所有组分都对硼酸-硼酸盐平衡反应。随后，C02转化为HCO^， H+释放(~10 s)， pH下降，最终达到平衡值8.2。计算出的C02中电子折叠时间的时间常数为13.1秒。这个值与第2.4.1节中讨论的体系计算的13.5秒值非常吻合，其中假定H+/ 0h和HCO3/CO3-的酸碱平衡已经建立。

使用对数时间轴的图2.4.11显示了与图2.4.10相同的结果。可以通过检查pH值来跟踪碳化合物的时间演变(图2.4.lid)。约10~7秒后(见

: 图2.4.12:硼化合物的弛豫。硼酸-硼酸盐平衡在大约10-4秒的时间尺度上响应扰动。

表2.4.2:碳酸盐体系的平衡和时间尺度。
过程	平衡	t”
复合	H20 ^ h + + oh "	10“7 S
P ro t y sis / H y d rolv sis	Co3 - + h + - hco j	10“7 s
硼化合物	B(0II)3 + H20 - B(OH) 4h	- 11+ 10”4秒
水合/ IIydroxylation	C02 + h20 h + + hco3	十年代

所示的时间尺度是各自平衡的特征(注意，这些平衡是通过几种动力学途径建立的，见正文)。

图2.4.lid中1号垂直虚线)pK增加是由于0H~ -f 1I+ H20(油-最初升高，因此H +被消耗)和HCO]"/CO2-平衡的重组。这种暂态(仅存在约10~ 3s，与最终的平衡状态不同)符合较低的HC03和较高的CO2-浓度(图2.4.11b和c)。硼化合物的弛豫导致IICO3、CO2-和pR在t = 10 4 s附近发生了微小的变化(图2.4.lid中垂直点虚线2)。最后，C02转化为HCO3(在10秒的时间尺度上)，所有组分放松到各自的平衡值(垂直虚线3)。对整个化学系统的概述分析可以识别所涉及的过程及其特征时间尺度(见表2.4.2)。

硼化合物浓度的时间变化如图2.4.12所示。由于硼酸-硼酸盐的平衡比扩散控制反应的平衡慢，B(OH)3和B(0H)4的浓度直到~ 10~4 s才有任何变化。随着pH值的升高，B(0H)3减少，B(0H)4增加。最后，硼化合物在C02/IIC03平衡时间尺度上松弛至其最终平衡值。

2.5接近同位素平衡:12C、13C和14c

我们现在转向封闭碳酸盐体系中碳同位素的平衡时间(对于开放体系，参见Broecker和Peng, 1974;Lynch-Stieglitz等人，1995)。尽管稳定同位素分馏4还没有详细讨论(这是第三章的主题)，在这一阶段包括碳同位素平衡的计算是非常方便的。这是因为该体系的分析类似于前几节中介绍的碳酸盐体系的化学平衡分析。不熟悉稳定同位素分馏的读者可以先看第三章。

在前面几节中，我们认为一个二氧化碳系统只包含一种碳同位素。因此，计算的弛豫时间反映了系统的化学平衡。当溶液中存在不同浓度的同位素时，较重的同位素反应速度较慢，导致碳物种之间的分馏效应。例如，C02到HC03的水化步骤(反应(2.3.36)正向)导致同位素“较轻”的HC03约为13%0。另一方面，脱水步骤(反应(2.3.36)向后)导致“更轻”的二氧化碳约为22%0 (O’leary et al.， 1992)。正向和反向反应的差等于平衡分馏介于C02和HC03之间，约为9%0 (Mook(1986)给出的平衡值在25°C时为8.97%o)。

12C、13C和14C反应的速率常数用kj2、kj3和kj4表示。由于所有相关的分馏效应最多在几个10%o的范围内，k}A和k}3与对应的k}2只有轻微的差异。文中强调，速率常数的略微不同对弛豫时间常数- 1的估计几乎没有影响

4在这里考虑的时间尺度上(分钟)，14C可以被视为一种稳定的同位素，因为14C的半衰期约为6000年。

实际上可以设置kj4 = KJS = k}2。当考虑不同的同位素时，最重要的新特征是该体系含有浓度非常不同的碳同位素物种。例如，13C原子和C原子的自然比例大约是1:99。含有不同同位素的化合物的偶联是由这些化合物与II+和OH-反应引起的。这引入了额外的时间常数。

同位素隔间

其中包括12 c。13 c。和14C组分，必须考虑9种碳物种，可分为3个隔间(参见第3.2.2节):
12co2 -•h12co:7	- 12二氧化碳”

13co2■-■ii' 'co.，	-■13 co2

14co2•—h14co:7	■“二氧化碳

室1

室2

室3

室1

室2

室3

这些隔间之间没有直接反应，因为每个同位素在反应过程中是保守的。因此，就碳同位素而言，有三个独立的体系。然而，该体系是通过H+和油进行耦合的。因此，当每个隔间的化学平衡达到时，同位素平衡也就达到了。

在开始分析系统的时间发展之前，有必要对14C做一些介绍性的说明。

放射性碳测定年代(14 c)

由于放射性碳的多种应用，在各自的调查中发生的14C的放射性可能在101至1013 dpm (g C)-1(每分钟每克碳的分解)之间。这个范围包括的自然活性，例如…大气二氧化碳和初级生产的测量(Steemann Nielsen, 1952)。大气CO的自然活性。海洋碳酸氢盐和活的植物和动物是(Mook, 1980):

W = * "iVTlnT *>/>»(±03 (2'5'46))

为了深入了解碳酸盐体系在不同环境下的行为，本节将研究不同浓度和pH值下海水中放射性碳组分的弛豫时间。计算方法类似于对稳定同位素13C的处理。由于14C的半衰期很长，在这里考虑的时间尺度上可以忽略放射性衰变引起的浓度变化。为了进行数值计算，必须将溶液中放射性碳的含量(通常用放射性来表示)转换为浓度。放射性通常以居里(Ci)或贝克勒尔(Bq)为单位。1贝克勒尔是指平均每秒发生一次衰变的放射性物质的数量。

1 Ci = 3.7 x 1010 Bq (disint。" 1)

根据溶液的给定活度(通常用//Ci kg-1表示)以及Ci和Bq的定义，可以计算出浓度。利用放射性衰变定律，推导出以下公式:

其中[c]为放射性碳的浓度(in /miol kg-1)， A为活度(/zCi kg"1)， t1/2 = 5730年(1.807 X 1011 s)为14C的半衰期(Mook, 1980)， NA = 6.022136 X 1023 mol"1为阿伏伽德罗常数。因此，初级生产(1201200±iCi)测量的典型活动对应14C([£14C02])的总浓度范围为2至20 /imol kg-1。

放松的时间

为了确定12C, 13C和14C化合物的弛豫时间，考虑以下反应:K+1

“c02 + h20 h + + h”coj (2.5.47)

VIC2 = ["CO^p+VfirCOg] (2.5.49) H20 ^ H+ + OH-;= [h +][oh ~] (2.5.50)

图2.5.13:海水中封闭二氧化碳体系(ECO2 ~ 2000 /¿mol kg-1, T = 25°C, S = 35)相对于碳同位素12C、13C和14C作为pH值函数的化学和同位素平衡松弛时间(实线)。当化学物质的浓度相似时(pH值约为7)，达到平衡的速度较慢。还显示了根据式(2.5.51)的曲线，可以用作近似值(虚线)。

计算中所用的C02与13C和12C的水化和羟基化反应速率的比值见表3.2.5，第3.2.6节。含14C的化合物的反应速率可以用式(3.2.34)和13C和12C的反应速率计算。如前所述，14C、13C和12C的速率常数略有不同，对计算出的时间常数影响很小(在这种情况下小于0.5 s， ~ 4%)。然而，在这里提到它们是为了使这幅图更完整。

该系统可以再次用动力系统的数学理论进行分析(见Zeebe等人(1999b))。当pH = 8.2、[£14C02] = 2和20 pmol kg"1时，体系的弛豫时间分别为13.849和13.848 s。因此，在这个范围内，弛豫时间实际上与14C的浓度无关。弛豫时间r随pE的变化如图2.5.13所示。在pE为7.14时，最大弛豫时间为24.4 s。对pE的依赖是由C02和HCO3转化途径不同引起的。在低pH值时，C02和H+的浓度较高，因此与HCO3和OH-的平衡(反应(2.5.47))很快实现。在较高的pH值下，HCOJ和OH-的浓度较高，因此与C02和H+的平衡(反应(2.5.48))很快实现。在所有化学物质浓度相近的pH范围内，平衡的实现较慢([H+]* % [OH"]*在pH值7左右)。

对整个系统进行分析，得到如图2.5.13所示的实体曲线。然而，它可以用一个简单的公式来近似:

- = (k+1 + [H+r + k_4 + k+4 [OH-]*)。(2.5.51)

如图2.5.13中的虚线所示。对于T = 25°C, S = 35的海水，r可写成:

t = (0.037+(2.66 x 104)(10- ph)+ 1.76 x 10

+ (4.05 X 103)(10-13-22)/(10-pH) _1

在pH = 8.2时产生r = 13.2 s(关于fc的温度依赖性，见表2.3.1)。公式(2.5.51)已在第2.4.1节中导出了小浓度SC02的C02平衡时间。事实上，式(2.5.51)也描述了这里所考虑的体系的平衡时间，这并不奇怪，因为它含有少量的14C。

综上所述，在所考虑的二氧化碳体系中建立化学和同位素平衡所需的时间约为分钟。弛豫时间实际上与溶液中放射性碳的含量无关，当浓度范围为2至20¿¿mol kg”1时(活度约为120-1200 /xCi)。

推导出放射性与浓度的换算公式(式(2.5.46))。注意，活度A与放射性原子总数N相关，关系式为A = -dN/dt = AN。

2.6扩散与反应

到目前为止，碳酸盐岩系统的动力学一直是在一个封闭、均匀的化学系统中讨论的。然而，在自然界中，我们通常必须处理异构系统。以海洋表层为例。空间浓度梯度是在海气界面通过降水/蒸发或藻类吸收营养物质而产生的。因此，该体系在浓度方面表现出非均质性。作为一种反应，化学反应和通过扩散进行的质量传递将倾向于降低这些浓度梯度。对这些过程的描述必须同时考虑反应和扩散，这导致了所谓的扩散-反应方程。

这里我们首先讨论平面上的一维扩散

继续阅读:稳定同位素分馏

这篇文章有用吗?

读者的问题

姆鲁国家公园EYOB
什么反应会产生二氧化碳和水?

3个月前
- 回复

有机物质的燃烧，如木材或天然气的燃烧，会产生二氧化碳(CO2)和水(H2O)。