IxciZi雷竞技csgo1116

其中ci是离子I在溶液中的浓度，zi是离子I在溶液中的电荷量。介质中存在的所有离子的总和，例如，对于纯NaCl溶液:

虽然NaCl是海水的主要盐成分，但海水和纯NaCl溶液的性质有很大不同。海水是不同电荷类型的电解质混合物的复杂溶液，其中必须考虑更多的离子，如Mg2+和SO4-(对于化学海水成分，参见表A.12.3，附录A)海水离子强度大约是0.7

我= ^ (Cl ~ 1 + (Na +) x 1 + x4 [Mg2 +] + [S02 ~] x4 + ...) « 0.7,

对应于a海水的盐度S ~ 35。海水离子强度可由盐度计算(DOE, 1994):

从图1.1.5可以明显看出，在30 < S < 40范围内，离子强度与S呈较好的线性函数关系，可以近似为I ~ 0.02 5。

0.85

0.85

图1.1.5海水中盐度与离子强度的关系。

盐度

图1.1.5海水中盐度与离子强度的关系。

盐度

活度系数

描述溶解在淡水和海水中的离子的化学行为的核心是它的活性。这个概念可以如下图所示(注意，这个图不是一个严格的类比)。假设有两辆汽车，其中一辆在纽约市高峰时段行驶，另一辆在夜间驶过死亡谷。在纽约的汽车会受到与街道上所有其他车辆相互作用的阻碍(对应于与溶液中存在的大量离子的相互作用)，而在死亡谷的汽车则可以自由移动(溶液被高度稀释)。有人可能会说，纽约交通中的汽车“活跃度”很低，而死亡谷中的汽车“活跃度”很高。表示溶液中离子的这种行为的化学量，实际上叫做活度。

化学种a的活性用{a}表示，与该化学种的浓度有关。[A]，由活度系数

理想情况下，活度系数为1.0。指所有溶质的浓度接近于零的无限稀释活度。需要注意的是，该定义指的是纯水中的参考状态，而海水中的pH值标度则以海水为参考状态(参见第1.3节和Wedborg等人(1999))。在简单电解质的稀溶液中，与理想行为的偏差是由远距离静电相互作用引起的。对于这些相互作用，可以近似地描述活性系数对离子强度的依赖关系

(见下文)。在海水中，情况更为复杂，因为(a)海水的离子强度较高;(b)因为存在各种不同的带不同电荷的离子。这导致了不同电荷类型的电解质混合物(如海水)中的离子配对和复合物的形成。例如，带负电荷的碳酸盐离子(CO2-)与带正电荷的Mg2+或Na+离子相结合，形成如NaCOg或MgCOg的离子对。海水中最重要的离子对平衡是(Skirrow, 1975):

Ca2+ + CO2”^ CaCOg Mg2+ + COg~ ^ MgCOg Na+ + C023~ ^ NaCOg Ca2+ + HCOg ^ CaHCOg Mg2+ + HCOg ^ MgHCOg

因此，除了由于与溶液中所有其他离子的静电相互作用而降低C03~离子的活性外，海水中的碳酸盐离子并不是“自由的”——它与带相反电荷的离子形成对。关于我们对交通类比的说明，这可能对应于纽约市交通中一辆拖着拖车的车辆。

化学计量常数(公式1.1.5和1.1.6)定义中HCOg和CO2的浓度是指总浓度，即自由离子+离子对;它们有时分别用[HCOgT]和[CO2^]表示(Skirrow, 1975)。

考虑到离子配对对活性的影响，讨论“自由”和“总”活度系数是有用的。在稀溶液中，自由活度系数和总活度系数之间没有差异，因为所有离子都被认为是“自由的”(即没有离子配对或复合物形成)。然而，在海水中，由于离子对的形成，总活度系数可能大大低于自由活度系数。

单个离子的自由活度系数，或简单电解质的单离子活度，可以使用Debye-Hiickel极限定律计算(参见，例如Stumm和Morgan, 1996):

log(7/) = -Az2 \fl I < 1(T2-3 (1.1.18))

或者戴维斯方程:

log(7/) = -Az2 [t^Jj ~ 0-2/j / < 0.5 (1.1.19)]

A = 1.82 × 106(el1)~3/"2。其中e»79为水的介电常数，T为温度(开尔文)。在25°C时，水的A约为0.5。离子的电荷表示为，I为介质的离子强度。使用公式中给出的近似。(1.1.18)和(1.1.19)，则可计算简单稀溶液的活度系数(表1.1.2)。要解决的问题是:这些近似值也可以用来计算海水中离子的总活度系数吗?

表1.1.2:Tc = 25°C稀溶液中某些离子的自由活度系数■)f。

离子强度:/ = 10"3 10"2 0.1 0.5 CI . .\a \HCO， .11'。

油”。B(0i1)7 0.96 0.90 0.77 0.69

Mg2+，S02-，Ca2+， c02 - 0.86 0.66 0.36 0.23

Po4”0.72 0.40 0.10 0.04

“利用Debye-Hiickel极限定律计算，公式(1.1.18)。”用Davies方程计算，Eq.(1.1.19)。

海水的离子强度约为0.7，仅略高于戴维斯方程所应达到的离子强度极限。因此，人们可能会想用戴维斯方程来计算海水中离子的活性。然而，如前所述，对于海水，Debye-Hiickel极限定律或Davies方程不再适用，因为它们只适用于稀释溶液和简单电解质(而不是不同电荷类型的浓缩溶液和电解质混合物)。海水中存在离子对和复杂形式，因此有必要考虑总活度系数。在包括海水在内的自然水体中，被广泛用于描述离子溶质总活度系数的模型是“离子对模型”(例如Bjerrum, 1926;Carrels and Thompson, 1962;Sillen, 1961;Millero和Schreiber, 1982)和“Pitzer化学平衡模型”(例如Pitzer, 1973;米雷罗和皮埃罗

1998)。对这些相当详细的模型的描述超出了本书的范围。最近，Millero和Pierrot(1998)发表了一个基于Pitzer模型的天然水域模型，与实测值相比，海水活度系数得到了良好的结果(表1.1.3:也与Millero相比，2001)。

16			第1章。平衡
表1.1.3:	:某些的总活度系数-ft		在Tc - 25°C和
S = 35。
离子	74(测量)”	(计算)	h 7j(戴维斯eq.)c
ci -	0.666	0.666 ^	0.69
Na +	0.668	0.664	0.69
H +	0.590	0.581	0.69
0 h -	0.255	0.263	0.69
HCO3	0.570	0.574	0.69
4 - B(哦)	0.390	0.384	0.69
Mg2 +	0.240	0.219	0.23
s02,	0.104	0.102	0.23
Ca2 +	0.203	0.214	0.23
天哪	0.039	0.040	0.23
h2po4 -	0.453	0.514	0.69
hpor	0.043	0.054	0.23
运动	0.00002	0.00002	0.04

a参考资料，见Millero and Pierrot(1998)。*Millero和Pierrot(1998)。

cFree活度系数，Davies方程，Eq.(1.1.19)。^分配值。

a参考资料，见Millero and Pierrot(1998)。*Millero和Pierrot(1998)。

cFree活度系数，Davies方程，Eq.(1.1.19)。^分配值。

在相同离子强度下，NaCl溶液与海水的基本区别是什么?

用式(1.1.17)和表A.12.3(见附录A)计算海水的离子强度。总离子强度中有多少百分比是Na+、CI-、Mg2+和SO2”离子的总和?

1.1.3热力学、混合和化学计量学平衡常数

为了描述水介质中的质子转移反应，使用了几个概念。这里我们只简要地总结与这些概念相关的不同平衡常数，也称为酸度或解离常数(回顾见Dickson, 1984)。碳酸的第二解离常数。A2，可以作为一个例子。

(1)质子转移反应的标准酸度或热力学平衡常数A’2:

完全用行为来表示:

从理论的角度来看，活动量是适当的平衡热力学.4然而，使用活性的一个严重缺点是，活性不像浓度那样容易测量(如果有的话)。在典型海水盐度下，从浓度到活度的转换需要相当费力和不确定的活度系数计算。幸运的是，平衡关系也可以用浓度来表示。

(2)海洋学中使用的一个有用的概念是基于所谓的混合常数，即浓度和活动同时发生:

其中aH在操作上是根据无限稀释公约定义的(关于这种方法的详细讨论，参见Dickson, 1984;Skirrow, 1975)。

(3)完全用浓度表示的常数是酸解离反应的经典质量作用积，也称为化学计量常数，如1.1节所述:

其中[H+]在操作上是根据恒定离子介质公约定义的。化学计量常数通常用K*表示。请注意，一些作者为了简单起见省略了星号(参见DOE(1994)和Millero(1995))。

在使用NBS缓冲液测量质子表观活度的基础上定义了一个表观常数。这些常数不再存在

4注意，浓度(而不是活性)是化学动力学中适当的量(见第2章)，因为反应速率取决于每体积碰撞分子的数量，因此取决于浓度(Lasaga, 1981)。

用于化学海洋学，因为所有常数都是用总质子尺度或海水尺度确定的(比较第1.3节)。下面由Skirrow(1975)引用的表观常数也适用于化学计量常数和混合常数。“离子对的形成”是表观常数不仅依赖于离子对的主要原因溶液的离子强度但对离子组成也有影响”(Skirrow, 1975, p. 76)。

1.1.4离子强度对pK*值的影响

在介绍了离子强度、活性和不同的酸度常数的概念之后，我们现在可以量化离子强度(以及盐度)对pK*值的影响，如前所述。

结合方程式。(1.1.20)和(1.1.22)，A'2可以表示为(注意{C02-} = 7cO2-[C02-]):

K;= K2 7hc°3"。(1.1.23)

从式(1.1.23)可以明显看出，较高离子强度的总活度系数的相对变化导致解离常数K2的变化。利用表1.1.3给出的7i值和25℃时I<2的淡水值10.33，可以估计出S = 35时海水中pK2的值(计算式(1.1.23)的负公对数):

M’2>海水- 10-33-loH0.590 x 0.039j = 8.94

接近实验测定值8.92 (DOE, 1994;表1.1.1)。

综上所述，考虑从淡水到海水的溶液，溶液中的离子数量增加，离子的相对比例发生变化，离子活性降低。由于不同离子的活度受到的影响不同，因此其活度系数之比会发生变化(参见式(1.1.23))。以上面讨论的pK2为例，CO3-的活度系数(从无限稀释时的1下降到海水中的0.039)比HC03的活度系数(从1下降到0.570)下降得更厉害。因此，海水中的pK2比淡水中的pK2更小(ii2更大)。因此，在相同pH值下，海水的CO2浓度(相对于CO2和HCO3的浓度)高于淡水(参见图1.1.4)。

1.1.5化学成分对pK*值的影响

一般来说，电解质(包括海水)的化学计量平衡常数取决于溶液的组成。幸运的是，海水的成分相当稳定。因此，pA'*'仅是P, T和s(或/)的函数。在海洋的某些区域(例如，波罗的海)，在孔隙水中或在许多实验室实验中盐的成分与标准海洋平均值不同。Ben-Yaakov和Goldhaber(1973)估算了随盐成分变化的钒酸盐含量。他们的方法使用了海水模型和计算程序，类似于bv Garrels和Thompson(1962)和Berner(1971)描述的方法。Ben-Yaakov和Goldhaber(1973)提供了灵敏度参数:

其中，AK *是K*由于组分i的相对浓度变化Acj/c-而引起的变化。根据已知的在海水中形成离子对的倾向，可以预期，镁具有最大的灵敏度参数:sA'*，Mg2+ = sfc*jMg2+ = 0.442(在19%的氯浓度下，对应的盐度为-34.3,T = 25°c)。例如，Mg2+浓度加倍，pK^将从5.86降低到5.80,pK*2将从8.93降低到8.77。盐的组成变化对平衡分压的影响将在练习1.5中进行研究。现在，建议直接从最先进的海水模型(如Millero和Roy(1997)开发的模型)计算pK*'n。

考虑温度为25°的海水。5 = 34.3, P = 1 bar, DIG = 2 mmol kg-1, TA = 2.35 mmol kg-1。计算CO2的平衡分压(提示:使用附录中给出的公式)。估算Mg2+离子自然浓度加倍时pCC>2的变化。

1.1.6平衡常数的选择

在这个阶段我们必须讨论一个领域碳酸盐化学我们觉得，就目前的状况而言，这有点令人不满意。碳酸、硼酸、水等的解离平衡常数已由不同的作者在不同的介质中测量，即天然海水和人工海水，以及在不同的pH值范围内(参见第1.3节和第13节)

使用解离常数计算碳酸盐系统不同作者给出的参数，得到的结果也不同。如果不考虑pH值尺度之间的转换，可能会产生特别大的差异。虽然有人试图就一组统一的常数和单一的pH值尺度达成一致(参见Dickson(1984)，联合国教科文组织(1987))，但这种方法迄今尚未成为标准。

与浓度计算相关的潜在问题的一个例子碳酸盐物种表1.1.4所示。让我们假设已经测量了样品的pH值和DIC，但测量时的pH刻度尚未报告。换句话说，目前尚不清楚使用的是海水尺度、总尺度还是自由pH值尺度-有关定义，请参阅第1.3节。当pH = 8.08, DIC = 2 mmol kg-1时，可以计算出三个尺度下的碳酸盐体系参数(表1.1.4)。海水和总比例尺之间的差异相当小(pC02为~ 10 /¿atm)，这两个比例尺和自由比例尺之间的差异是巨大的(pC02为> 100 /iatm)。需要强调的是，计算得出的差异是由于测量pH值时所用的比例尺尚未确定。如果测量中使用的pH值标度是已知的，计算的pH值将被转换为正确的pH值标度(对应于解离常数的标度)，那么在每种情况下都会得到完全相同的结果。但是，此场景需要使用一组常量，请参见下面。在实践中，人们可以使用任何pH值来计算-关键的一点是pH值和使用的解离常数必须一致。

表1.1.4:在测量pH值的尺度未知(pH = 8.08, DIC = 2 mmol kg"1, S = 35, Tc = 25°C)时，计算出的碳酸盐体系参数

pH值范围	pH值	pC02	二氧化碳(aq)。	HCO3	公司§”
		juatm	害怕imol公斤	害怕/摩尔公斤	/ imol公斤
海水	8.08	354	10．0	1735	255
总计	8.08	363	10.3	1739	250
免费的	8.08	478	13.6	1786	201

在所有计算中都使用了Roy等人(1993a)转换为不同pH值的常数(见第1.3节)。

在所有计算中都使用了Roy等人(1993a)转换为不同pH值的常数(见第1.3节)。

即使在相同的pH值范围内进行计算，由于使用的解离常数由不同的作者确定，也可能发生值的差异。然而，这种差异通常比上述情况要小。表1.1.5显示了由DIC和TA计算的碳酸盐物种浓度值，使用常数(全部转换为海水尺度)称为“Hov”。“Harisson”和“Mehrbach”(定义见表1.1.5的脚注)。在这个特殊的例子中，pC0.2的计算值相差30 //atm。

最近，研究证明，在从DIC和TA中测定pC02时，使用Mehrbach常数进行碳酸的解离可以获得最佳结果(Wanninkhof等人，1999;Johnson等人，1999;Lee等人，2000年;Lueker等人，2000)。因此，在这种特殊情况下可以使用梅尔巴赫常数，这是我们推荐的。然而，我们应该使用哪一组常数，例如，从pH和DIC确定pC02，或从p('()和TA确定[CO^-] ?事实上，Mehrbach常数在上面提到的重要情况下做得很好，并不意味着它们在所有情况下都是这样。正如Wanninkhof et a.1。(1999)说:“……使用Mehrbach常数的pC02(SST)和pC02(TA, DIC)之间的良好一致性并不一定意味着这些常数与其他碳系统参数的最佳一致性”。 Here is the problem: when calculating various parameters of the carbonate system using different input variables (as is done in this book, for example) one cannot use different sets of constants since this would lead to inconsistent results.

表1.1.5:采用不同作者给出的解离常数计算的碳酸盐体系参数(DIC = 2 mmol kg"1, TA = 2.35 mmol kg"1, S = 35, Tc = 25°C)。

作者	Pn慢波睡眠	pC0.2 //在m	C02(aq.) //mol kg-1	/ /摩尔公斤	Co2 " //mol kg-1
罗伊' 1	8.08	354	10．0	1735	255
Hansson4	8.10	343	9.7	1739	251
Mehrbachc	8.11	327	9.3	1742	249

Roy et al. (1993a)转换为海水尺度(Millero, 1995)。4Mehrbach等人(1973)改装的Dickson和Millero(1987)。cHansson (1973b)，由Dickson和Millero(1987)改装。

Roy et al. (1993a)转换为海水尺度(Millero, 1995)。4Mehrbach等人(1973)改装的Dickson和Millero(1987)。cHansson (1973b)，由Dickson和Millero(1987)改装。

在选择一组特定的解离常数时应记住的另一个问题是，确保所有常数都是在相同的介质中确定的，即天然或人工海水。“梅尔巴赫常数”是在天然海水中测定的，而“罗伊常数”和“汉森常数”是在人工海水中测定的。很可能这就是为什么在海洋中，即在天然海水中进行测量时，梅尔巴赫常数表现良好的原因。碳酸盐体系参数的精确计算除碳酸的解离外，还包括水的解离、硼酸、硫酸氢、氟化氢、磷酸、硅酸等。为了实现计算的内部一致性，所有使用的常数应在单一介质中确定，即在天然海水或人工海水中确定。

关于本书中给出的计算，我们决定使用DOE(1994)中总结的常数集，包括碳酸的解离常数，称为“Roy”，数值见附录。这些在人工海水中测定的常数均以总氢离子浓度(即总pH值，见第1.3节)表示，并以摩尔/千克溶液为单位。基于上述原因，这一套似乎最适合我们目前的目的。然而，我们注意到，例如梅尔巴赫常数在特定情况下可能更合适。

这里所描述的问题将来能得到解决是非常可取的。我们认为，实现这一目标的主要步骤是(a)共同体就单一pH值尺度达成协议，以及(b)高精度确定天然海水中的所有相关解离常数。

1.1.7 CaC03溶解度与海水饱和状态

海洋中碳酸钙(CaC03)的形成和溶解是全球碳循环的重要参与者，在不同时间尺度上与大气二氧化碳的控制密切相关。例如，目前在大气中积累的人为co2被认为大部分被海洋吸收，并最终通过与海洋沉积物中的CaC03反应而中和(所谓的化石燃料中和，例如Broecker和Takahashi, 1977;Sundquist, 1986;Archer et al.， 1998)。在碳酸钙形成和溶解的背景下，一个决定因素是海水中的CaC03饱和状态，这是碳酸盐离子浓度的函数。换句话说，固态和溶液之间的平衡是由海水的腐蚀性控制的。因此，海水的CaC03饱和状态是海水碳酸盐化学的一个重要方面。

本节讨论了CaC03在海水中的溶解度、海水饱和状态以及CaC03在海洋沉积物中的分布。CaC03的产生对碳酸盐系统的影响在第1.6.1节中进行了检验，而在第1.6.5节中提到了未来大气中二氧化碳增加对钙化的潜在影响。如需进一步阅读，请参见e.g. Berger et al. (1976)， Broecker and Peng (1982)， Mucci (1983)， Morse and Mackenzie(1990)。Holligan和Robertson (1993)， Millero(1996)。

绝大多数海洋碳酸钙是由分泌钙质或文石壳和骨骼的生物产生的。大洋中方解石的主要生产者是球石藻和有孔虫，而最丰富的远洋文石生物是翼足类。(关于包括珊瑚礁和其他环境在内的CaC03生产的综述，见Milliman. 1993;Milliman和Droxler, 1996)方解石和文石矿物均由(a('()，_。但矿物学不同。方解石的晶体结构是菱形的，而文石的结构是正交的(参见Hurlbut(1971)或Reeder(1983))。两种矿物的不同结构导致了不同的物理化学性质(表3.2.4，第3章)，其中溶解度是最重要的。

化学计量溶解度积定义为:A';= [Ca2+]sat x [C02"]sat'， (1.1.24)

其中，[C03~]sat是指饱和CaC03的海水溶液中平衡总(自由+络合)碳酸盐离子浓度。在一定的温度、盐度和压力下，文石和方解石的溶性分别为K* = 10~6’19和10~b’3’mol2 kg-2 (t = 25℃，5 = 35,P = 1 atin)。Mucci(1983)测定文石和方解石K*的计算公式见附录A. 10。在平衡时，溶液中Ca2+和co2浓度的乘积由等式(1.1.24)的左边给出。如果[Ca2+] X [CO2-]大于这个值，则溶液相对于CaC03是过饱和的，否则，溶液是欠饱和的。海水Ca.C03饱和状态fi表示为:

其中[Ca2+]sw和[C03]sw分别为海水中Ca2+和CO的浓度，K*为温度、盐度和压力原位条件下的溶解度积，fi > 1对应过饱和，0 < 1对应欠饱和。

在公海中，[Ca2+]的变化相当小，与盐度的变化密切相关。因此，CaC03的饱和状态主要由碳酸盐离子浓度决定。表1.1.6总结了饱和时碳酸盐离子浓度的值，[CO2-]^?对于方解石和文石作为温度和压力的函数(Mucci, 1983)。

表1.1.6:S = 35和[Ca2 +] = 10.28 mmol kg-1时的饱和碳酸盐离子浓度(cf. Broecker和Peng, 1982)。”

温度	压力	tcoru
(°C)	(atm)	(/ imol公斤)
		方解石霰石
25	1	63 - 41.6
2	1	67 - 41.9
2	250	107 - 69.4
2	500	雷竞技csgo167 - 111.7

Mucci(1983)后I\'*p的值。Millero(1995)之后的压力修正。公式见附录A. 10。

Mucci(1983)后I\'*p的值。Millero(1995)之后的压力修正。公式见附录A. 10。

碳酸钙是一种不同寻常的盐:温度越低溶解度越高!温度对溶解度的影响很小(见表1.1.6)。更重要的是，溶解度随着压力的增加而增加。这对海洋沉积物中CaC03的分布具有重要意义。假设海洋深处温度恒定，[C03~]sat随压力增大而增大，因此随海洋深度增大而增大(图1.1.6)。

原位和饱和碳酸盐离子浓度之间的交叉称为饱和层或饱和深度/层位。从表层沉降到深海的碳酸钙主要保存在饱和水层以上的过饱和水中，在饱和水层以下的不饱和水中开始溶解因此，我们可能会认为海底是一个有冰雪覆盖的山脉的景观(silen, 1967;Broecker和Peng, 1982)。海底的上层部分，如脊顶，覆盖着浅色的CaC03，而海底的CaC03则覆盖着浅色的CaC03

5这种描述是高度简化的，详见Broecker and Takahashi(1978)、Broecker and Peng(1982)或Morse and Mackenzie(1990)。

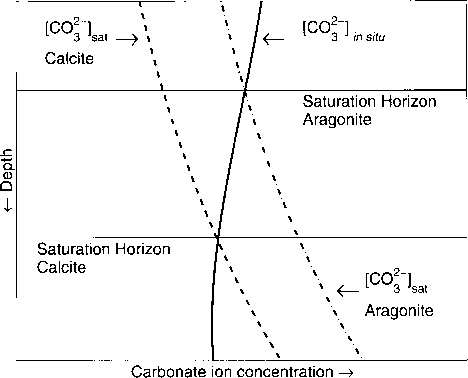
图1.1.6:海洋中方解石和文石饱和层(SH)的说明(继Broecker和Peng, 1987年之后)。随着压力的增加，方解石和文石的溶解度也随之增加([OOj~] J.方解石和文石的原位碳酸盐离子浓度(固体曲线)与方解石和文石的饱和浓度(虚线曲线)之间的交叉决定了不同矿物相的饱和水平。

图1.1.6:海洋中方解石和文石饱和层(SH)的说明(继Broecker和Peng, 1987年之后)。随着压力的增加，方解石和文石的溶解度也随之增加([OOj~] J.方解石和文石的原位碳酸盐离子浓度(固体曲线)与方解石和文石的饱和浓度(虚线曲线)之间的交叉决定了不同矿物相的饱和水平。

山谷中大多不含Ca和C03，覆盖着颜色较深的粘土矿物。

图1.1.7显示了北太平洋和北大西洋海水的方解石和文石饱和状态。表层海水相对于方解石和文石的过饱和程度分别约为6倍和4倍。过饱和随着深度的增加而减小，直到越过0=1这条线。文石的交叉发生在较浅的深度，因为文石比方解石更容易溶解。此外，北太平洋的饱和状态小于北大西洋。下面将讨论这些区域差异。

所观察到的深度溶解速率迅速增加

图1.1.7:海水饱和状态fi与方解石(a)和文石(b)的深度函数关系Q由公式(1.1.25)和来自北太平洋和北大西洋的DIC-TA剖面计算。虚线将过饱和区域(f2 > 1)与欠饱和区域(Q < 1)分开。数据来自WOCE P14N部分，Stn. 70 (F. Millero和Ch. Winn)和WOCE A05部分，Stn. 84， (F. Millero和S. Fiol)，http://cdiac.esd.ornl.gov/oceans/CDIACmap.html．

图1.1.7:海水饱和状态fi与方解石(a)和文石(b)的深度函数关系Q由公式(1.1.25)和来自北太平洋和北大西洋的DIC-TA剖面计算。虚线将过饱和区域(f2 > 1)与欠饱和区域(Q < 1)分开。数据来自WOCE P14N部分，Stn. 70 (F. Millero和Ch. Winn)和WOCE A05部分，Stn. 84， (F. Millero和S. Fiol)，http://cdiac.esd.ornl.gov/oceans/CDIACmap.html．

在沉积物中被称为溶跃层。溶跃层一词源于希腊语中表示溶液和倾斜的词——类似于温斜:见Berger(1968)。溶跃层因此分离了保存较差和保存较好的CaC03组合。由于文石的溶解度高于方解石，所以文石溶跃层通常比方解石溶跃层深度低。文石溶跃层在太平洋可浅至500米，在大西洋可浅至3公里。方解石溶跃层在太平洋和印度洋约4公里处发现，在大西洋4至5公里处发现。太平洋和大西洋溶跃层深度差异的原因是太平洋深水区碳酸盐离子浓度低于大西洋深水区(co2含量较高)。也就是说，太平洋深水的腐蚀性更强(图1.1.7)。这主要是海洋环流和生物活动相互作用的结果:太平洋的深水比大西洋的深水“更古老”，因此从有机物的再矿化中吸收了更多的二氧化碳，从而降低了其碳酸盐离子含量。一个水团的年龄在这里指的是从它最后一次接触大气层以来所经过的时间。

沉积物中几乎不含碳酸钙的深度称为碳酸钙补偿深度(CCD)。通常在左斜斜与CCD之间存在一个过渡带，在该过渡带中，沉积物中的碳酸钙含量随着深度的增加而逐渐降低。过渡区可以大到几百米，这与('a('())的供应率有关。即表层海洋的产量和CaCO的动力学;!深海溶解(Broecker and Peng, 1982;莫尔斯和麦肯齐，1990;Millero。1996)。

我们将在接下来的章节中回到碳酸钙的生产和溶解。稳定的同位素分馏海洋碳酸钙中碳、氧和硼的含量将在第三章中讨论。

继续阅读:[boh4

这篇文章有用吗?

0 0