动力学

在第一章。的性质碳酸盐系统热力学平衡进行了研究。演示了如何利用这些特性来了解由人为co2入侵海洋或形成CaC03等过程引起的海水化学变化。碳酸盐体系的平衡性质适用于这些过程的描述，因为所涉及的特征时间和长度尺度是月到年，米到公里。然而，在较短的时间尺度上，必须考虑碳酸盐体系的不平衡。在第2.4节中将说明，建立化学平衡所需的时间约为一分钟。因此，比这更快的过程不能被平衡概念充分描述。一个例子是化学物质在长度尺度上的运输或供应，其中化学转化和扩散是10~3 m的主要机制。例如，在海洋-大气界面的扩散边界层内(空气-海洋气体交换)或在较大的海洋浮游生物的微环境内。

本章介绍了化学动力学的一些基本特征及其数学描述(第2.1节)。然后总结了碳酸盐岩体系速率常数的数值及其温度依赖性(第2.3节)。详细描述了碳酸盐岩体系的动力学(第2.4节)，包括对系统弛豫走向平衡所涉及的时间尺度的分析。在此背景下，还考虑了稳定的碳同位素12C、13C和14C(第2.5节)。最后，讨论了平面几何和球面几何中的扩散反应方程(第2.6节)。

这是不可能讨论动力学的所有方面碳酸盐化学以及它们在这本书中的应用。如需进一步了解海洋和大气之间的二氧化碳交换、CaC03沉淀/溶解动力学以及生物体内C02动力学的生化和生理方面，请参见例如:Emerson(1995)、Wanninkhof(1996)、Mucci等人(1989)、Wollast(1990)、Morse和Mackenzie(1990)、Forster等人(1969)。

2.1动力学的基本概念

化学动力学研究化学性质随时间的变化。不同于化学平衡，在化学平衡中，根据定义，反应物的浓度不随时间变化，化学动力学描述了反应过程中浓度的变化过程。化学动力学还在分子水平上研究从一种化学物种到另一种化学物种的转变细节。有趣的是，即使在化学平衡状态下，反应也随时都在发生——其独特的性质是正向反应和反向反应的速率相等。在这个意义上，热力学平衡可以被认为是化学动力学的一个特殊情况，其中系统已接近稳态。然而，这里很重要的一点是，在化学动力学中浓度是适当的量，而在热力学中活度是基本的量(参见第一章)。在动力学中使用浓度是因为反应速率取决于每体积碰撞分子的数量，因此也取决于浓度(Lasaga, 1981)。

在化学反应中，化学物质a可能与物质B反应生成C

例如，质子和氢氧离子结合形成水:

描述反应时间发展的核心是反应速率，我们将其记为r。对于(2.1.1)反应，a的消耗速率由a对时间的导数给出:

h++ OH" -►H20或C02的羟基化反应:C02 + OH" - > HCO3。

注意，负号表示反应速率为正。r的单位是浓度/时间。例如mol kg- 1s -1。通常，反应速率是反应物浓度的函数。在简单或基本反应的情况下，反应速率与个别浓度的代数幂的乘积成正比，例如:

r = a [a]1 [B]1 = k [a][B]。(2.1.3)

比例常数k称为速率系数或速率常数。式(2.1.3)在数学上表达了反应A + B -»C'中A的消耗速率与A和B的浓度成正比。这可以通过考虑反应发生的体积来说明。如果A和13的浓度高，A和B分子相遇并最终发生反应的概率就高，而当浓度低时则相反。

速率常数k的单位取决于反应的顺序(见下文)。在考虑的例子(式(2.1.3))中，k的单位是kg mol-1 s-1。这是因为右边的单位必须等于左边的单位(mol kg- 1s -1)由于[A] X [B]的单位是摩尔2千克-2，所以k的单位必须是千克摩尔-1 s-1，从而得到摩尔千克-1 s-1的总单位。另一方面，根据下面的速率定律，k的单位是s"1。

为了说明化学反应的速率，我们考虑式(2.1.3)，其中a = C02, B = 0H~。采用典型浓度[C02] = [OH-] = 1 × 1CT5 mol kg-1, pR = 8.2, 25℃，速率常数为~ 4000 kg mol-1 s-1时，反应速率为4 × f0-7 mol kg-1 s-1。因此，在f秒内，4%的二氧化碳和OH-发生化学反应，换句话说:二氧化碳和OH-的周转时间约为25秒。与H+和OH-的重组反应(H+ + OH- - >■II20)相比，这是一个非常慢的反应速率，其速率常数k为10nkg mol- 1s -1的数量级。在pll = 8.2和25℃时，反应速率为r = k x [11+] x[油

= 1011 × 6.3 × 10-9 × 1 × 10-5 = 6.3 × 10~3 mol kg"1 s-1

也就是说，在1千克海水中，6.3 × 10-3摩尔OH"在1秒内发生化学反应。这个量等于630倍的OH-的总浓度OH-的周转时间是1 /630秒。

当考虑可逆反应时，正向和反向反应的速率常数是描述动力学的必要条件:

如果速率定律为:

M = _*+[A] + k_[B]则平衡常数K*为:

因为在平衡时d[A]/df = 0。式(2.1.4)是反应平衡常数(通常用大写K*表示)与速率常数(用小写&'s表示)之间的基本关系。

由于反应速率与[A]1和[B]1(1 + 1=2)的乘积成正比，故将(2.1.1)反应称为两个不同物种之间的总体二级反应。但是，对于A和B这两种反应物，(2.1.1)反应都是一级反应。一般来说，根据速率定律roc [A]m[B]n，反应的总阶为m + n

在反应物A中为二级，在反应物B中为一级，总级数为3。该反应的速率定律可以写成:

r = _1 djA] =®= (2.1.5)

在这个例子中，假定反应的顺序可以从反应的化学计量学直接推断出来。不幸的是，这只适用于简单或基本的反应。任何反应，即使是单分子或双分子的反应都不能假定为先验的基元。例如，反应Br2 + H2 ^ 2HBr的速率表达式为r =

k [H2][Br2]1

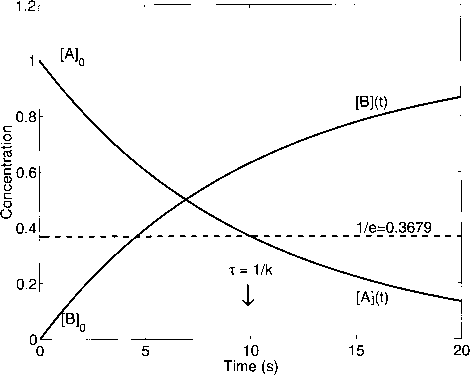
图2.1.1:反应A -»•B中A和B浓度的变化。速率常数k = 0.1 s-1的倒数是反应的特征时间尺度或衰减时间r(见正文)。

(Moore和Pearson. 1981)，因为该反应涉及一系列复杂的步骤。一般来说，反应级数是一个实验确定的量，也可以取非整数值。然而，对于一些反应，它如下:

n1Al + n2A2 +…+ nNAN - > rn^ij + m2B2 +…+ mMBM，则速率定律为:r = HAirfA^-tA^H。

当从理论上和实验上研究化学动力学时，化学物质浓度随时间的变化是非常有趣的。这些变化的数学描述是基于微分方程的解。(2.1.3)及(2.1.5)。以简单反应k为例

对此，利率定律如下:

A要解的微分方程为:

这是一个众所周知的数学方程，出现在很多问题中，比如放射性衰变，光吸收和更多。它说的是一个量的变化与这个量本身的值成正比。指定A和B浓度的初始条件，即[A]0和[B]0，解为(见习题):

[B](i) = [B]0 + [A]0 {1 - exp(-kt)}。

[A]和[B]在初始条件[A]0 = 1和[B]0 = 0(任意单位)下的时间发展如图2.1.1所示;速率常数是k = 0.1 s_1。A的浓度呈指数下降，而[B]的浓度呈指数增加，并在t -oo时趋近于1.0的渐近值。10s后A的浓度达到初始浓度的37% (- 1/e)左右，对应于以时间为单位的速率常数(r = 1/ k)的倒数这个所谓的衰减时间是一个非常有用的量，它描述了一个接近平衡的系统的松弛时间。

我们将在第2.4节回到反应动力学中微分方程的解，其中将讨论描述海水中碳酸盐化学动力学的动力系统的解。其他反应系统的各种例子及其数学解的配方可以在教科书中找到，如Steinfeld等人(1999)和Atkins(1998)。

解释式(2.1.5)中出现的因子1/2。练习2.2 (**)

(2.1.6)式的解可以通过分离变量得到:

1如果衰减是指数级的，我们也可以计算出达到平衡值99%的时间，大约是松弛时间的4.6 - ln(O.Ol)倍。

2.2速率常数的温度依赖性

在许多化学反应中，反应速率随着系统温度的升高而急剧增加。这种行为主要是由于分子的平均能量较高，导致每个时间间隔的反应次数较多。在生物系统的代谢率中也观察到类似的行为，因为温度也会影响酶催化反应。然而，大多数生物系统都有最佳温度，超过该温度酶将不起作用(£40°C)。这是因为高温使酶失活，最终使所有蛋白质在120°C以上变性(例如Beck等，1991年)。温度和酶途径速率之间的关系用所谓的Q10因子表示(见下文)。

在非酶化学反应中，反应速率是反应物浓度和速率常数的函数。由于浓度与温度无关，对温度的依赖关系用速率常数表示。温度和速率常数之间的关系通常可以用阿伦尼乌斯方程拟合:

其中A被称为指数前因子或阿伦尼乌斯因子，i?= 8.3145 J mol-1 K_1为气体常数，T为绝对温度(开尔文)，Ea为活化能(见下文)。

速率常数随温度的增加是Ea的函数。这可以通过比较2点时速率常数的值来证明不同的温度，例如在15°C和25°C。速率常数在/和T2处的比值为:

75 100

图2.2.2:示意图

阿伦尼乌斯的插图

图2.2.2:示意图

阿伦尼乌斯的插图

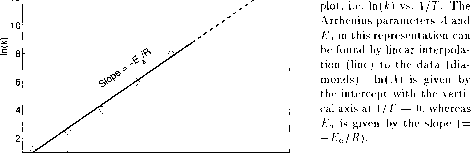
若活化能Ea为70 kJ mol-1，则比值约为3。换句话说，速率常数在15°C和25°C之间增加了3倍。如上所述，生物系统中酶促反应速率的相应增加用Q10因子表示，Q10因子表示温度每升高10°C的增加速率。因此在这个例子中Q10大约是3。

表明In(k)与1/T之间存在线性关系，由此可确定Arrhenius参数a和活化能Ea(图2.2.2)。

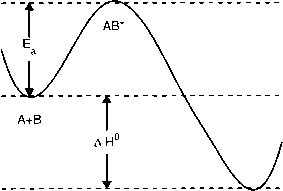
启动反应需要活化能。为了从反应物中形成产物，不仅需要反应分子相互碰撞，而且总动能要足以克服活化能的势垒。图2.2.3说明了反应A + B -►c的情况，由于反应焓AH0为负，反应是放热的，即在整个反应过程中，热量被释放到周围环境。然而，为了形成活化的络合物或过渡态AB*，首先必须提供活化能Ea(参见第三章第3.1.3节)。例如，气体分子的平均动能来自于每个分子以其特定速度运动的结果。在一定的温度下，分子表现出一定的速度分布，称为麦克斯韦-玻尔兹曼分布。有ln(k) = ln(a) - EJRT

CD c路

反应坐标

图2.2.3:反应a + B -►c的能量图解。随着反应沿反应坐标进行，最初必须提供活化能Ea以形成过渡态AB*。整个反应是放热的因为反应焓AH是负的。

大量分子的速度(绝对值)接近某一平均速度，有的比平均速度高，有的比平均速度小。只有那些具有足够能量克服Ea的分子才有可能发生反应(图2.2.4)。由于分子的平均动能随温度而增加，现在很清楚为什么反应速率随温度而增加，因为有更多的分子有足够的能量来反应。

关于酶催化反应，有趣的是，酶的关键功能是降低过渡态的能垒。因此，更多的分子被允许超越能量势垒，从而加速反应。即使只有微量的酶，也能使化学反应加快几个数量级。如果没有活跃在生物体绝大多数代谢途径中的酶，化学反应就会发生得太慢，无法维持生命。

速率常数的温度依赖性已被测量:k =

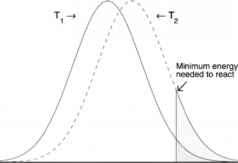
图2.2.4:不同温度下每个分子的能量含量示意图在较高的温度Th时，比在较低的温度Ti时(深色阴影区)，更多的分子具有进行反应所必需的能量(浅色阴影区)。这导致了反应速率的增加。

每分子能量

图2.2.4:不同温度下每个分子的能量含量示意图在较高的温度Th时，比在较低的温度Ti时(深色阴影区)，更多的分子具有进行反应所必需的能量(浅色阴影区)。这导致了反应速率的增加。

每分子能量

(5.0, 6.8, 8.6, 10.7, 12.5) x 106公斤摩尔“1”1在T =(4、6、20、25、31)°C。用阿伦尼乌斯方程拟合数据，确定反应的指前因子和活化能。

2.3碳酸盐体系的反应和速率常数

碳酸盐岩体系的动力学速率常数在动力学中的作用与热力学中的解离常数类似。因此，速率常数对于定量描述碳酸盐体系的反应动力学是非常重要的。本节的目的是提供文献中报告的速率常数及其讨论的摘要。相对于对海水中碳酸盐体系解离常数的广泛研究(见附录A)，迄今为止对海水中动力学速率常数的研究很少。其中一些常数是有争议的(见第2.3.2节和附录C.6)，硼酸-硼酸平衡的速率常数在海洋化学和化学海洋学中是广泛未知的。因此，当前部分包括工作知识的发展，而不仅仅是良好的工作知识。速率常数的值是本章后面几节讨论的基本量。

如第一章所述，碳酸盐体系的热力学平衡可以用以下关系式来描述:

二氧化碳	f 1 i20	- h++ hco3	(2.3.8)
二氧化碳- - - - - -	+ 2 +	- ii ('07	(2.3.9)
	1 i20	- h + + oh "	(2.3.10)
B (OH) 3	f水	= b (oh)7 + h +。	(2.3.11)

利用质量作用定律，可以得到平衡状态下每种化学物质浓度的信息。不幸的是，平衡(2.3.8)-(2.3.11)没有提供关于建立平衡所涉及的反应或反应机制的信息。与平衡(2.3.8)-(2.3.11)相关的反应机理和速率常数将在以下章节中逐步介绍。

2.3.1二氧化碳的水化作用

首先，我们将讨论二氧化碳水合作用(详见Kern(1960)和Edsall(1969))。反应方案可表示为式(2.3.12)(cf. Eigen et al.， 1961)。请注意，与二氧化碳相比，碳酸H2C03总是以非常小的浓度出现。因此状态(II)几乎没有被占用

继续阅读:二氧化碳的水

这篇文章有用吗?

0 0