循环的机械论观点

我们能在多大程度上解释观测到的大气环流的主要特征，其基础是由太阳强迫中的纬度梯度驱动的大气的简单流体动力学表示?这里的重点是“简单”。实际上，地球表面是非常不均匀的:有巨大的山脉扰乱了流动，海洋和大陆之间有很大的对比(例如，温度和表面粗糙度)。但是，为了简单起见，我们将忽略表面条件的这种变化。我们还忽略了季节和日变化，并假设太阳下点(图5.3)在一年中在两个热带地区之间移动，但赤道处的太阳输入最大。因此，我们将考虑纵向均匀的旋转行星(在其他方面与地球类似)上的大气对纬度梯度加热的响应。我们将看到，观测到的环流的大体特征确实可以在这个基础上得到理解;稍后，在第8.5节中，将简要讨论这种方法引入的缺点。

因此，我们问轴对称大气如何响应轴对称强迫，赤道的太阳加热比两极更强。似乎可以合理地假设响应(即诱导循环)将是类似的轴对称。事实上，这一假设最终为我们提供了热带环流的定性合理描述，但很明显，它在热带外大气中是不成立的，在那里，流体动力的不稳定性破坏了对称性。

8.2.1.热带哈德利环流

如果地球不是旋转，是由环流驱动的极点吗赤道的温度区别很明显，暖空气在低纬度上升，冷空气在高纬度下沉，这是Hadley首先提出的，如图5.19所示。但是，如图5.20和5.21所示，实际情况并非如此。我们确实在热带看到了经向环流，但下沉运动位于纬度±30°左右的亚热带地区。事实上，下面的考虑告诉我们，一个巨大的轴对称子午细胞从赤道延伸到极点在一个快速旋转的行星上是不可能的，比如地球。

如图8.3所示，考虑一个环绕地球的空气圈，它位于大气的上层向极地流动的内部，并被平流哈德利环流．因为这种流动假设是轴对称的，也因为在上层流动中，摩擦力可以忽略不计，远高于近表面边界层，绝对角动量将被环守恒，当它移动。单位质量的绝对角动量为(回想一下我们在第6.6.1节中对径向流入实验中角动量的讨论)

A = Qr2 + ur，第一项是行星自转的贡献，第二项是相对于地球的东风u，其中r是到地球旋转轴的距离。因为r = a cos p，

A = Qa2cos2p + ua cos p. (8-1)

现在，假设u = 0在赤道(图5.20显示这是一个合理的假设在赤道对流层上部)。那么绝对角

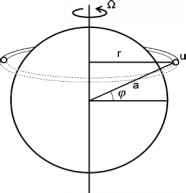
图8.3。在纬度p处以u速度向西- >向东吹的气流环的示意图。假定该气流环是由保存角动量的哈德利环流向极方向的气流平流形成的。

当然，在现实中，太阳强迫在正午前后和夜间的区域之间存在强烈的瞬时纵向变化。然而，除了非常接近地表的地方热惰性大气的温度会抑制这些波动，昼夜之间的温度变化很小。因此，忽略日变化是一个合理的近似。

赤道处的动量就是A0 = q2。当空气环向极地移动时，它保持这个值，所以当它到达纬度p时，它的绝对角动量为

A = Qa2 cos 2p + ua cos p = A0 = Qa2。

因此，环将获得一个向东的速度

问(a2 - a2 cos2p) sin2p, u (p ) = _______ 1 = Qa。(8 - 2)

请注意，当我们意识到r = a cos p时，这与我们的径向流入实验的Eq. 6-23直接类似。公式8-2意味着远离赤道的不现实的大风，纬度为(10°，20°，30°)，u(p) = (14,58,130) m s-1，当然，风在p ^ 90°时变得无穷大。基于物理上的合理性，很明显，这种轴对称循环不能以Hadley设想的方式一直延伸到极点(并在图5.19中概述);它必须在到达极点之前的某个地方终止。循环能延伸到多远(根据理论)取决于许多因素

考虑循环的上层分支，如图8.4所示。在赤道附近，f很小科里奥利效应相对较弱，角动量约束不那么严重，赤道大气的作用就好像地球在缓慢旋转。然而，当空气远离赤道时，科里奥利参数变得越来越大，在北半球，风向右转，导致气流的西风成分。在向极地的范围内哈得来环流圈，那么，我们期望找到一个强大的向西流，正如我们所做的那样(见图5.20)。这种亚热带急流是

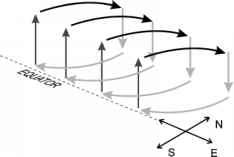
图8.4。哈德利环流示意图(只显示环流的北半球部分;赤道以南有一个镜像环流)。高空向极流诱发西风带;低空赤道气流诱发偏东气流。

这在很大程度上是由哈德利环流从赤道带来的大绝对值角动量平流所驱动的，从公式8-2和图8.4中可以明显看出这一点。气流在哈德利环流槽的副热带边缘减弱，沉入副热带高压(图7.27非常明显)，然后以低空回到赤道。在这些低水平科里奥利加速度，在北半球再次使赤道气流向右转，产生信风，在北半球向东北吹(在南半球向东南吹)(见图7.28)。这些风不像对流层上层那么强，因为它们被作用在近高空的摩擦所缓和表面流．事实上，如上所述，一定有低空西风带存在。在平衡状态下，整个大气的净摩擦阻力(严格地说，扭矩)必须为零，否则大气的总角动量就不能稳定。(固体地球的角动量会发生补偿变化，一天的长度就会漂移。)

2例如，如果地球旋转得更慢(或更快)，在其他条件相同的情况下，哈德利环流就会向极地延伸得更远(或更远)。

事实上，由于大气和下垫面之间的角动量转移，一天的长度确实有细微的变化。例如，在季节性的时间尺度上，一天的长度会有大约一毫秒的变化。一天的长度每天大约变化0.1毫秒!此外，这些变化可以归因于地球和大气之间角动量的交换。

沙漠(等距无调性地带)

图8.5。原理图Hadley环流及其相关的纬向流表面循环．

沙漠(等距无调性地带)

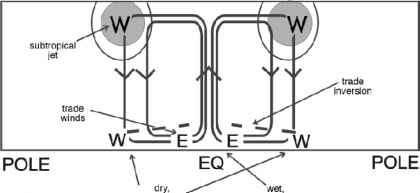
图8.5。哈德利环流及其相关的纬向流和地表环流的示意图。

因此，如图8.5所示，在我们的轴对称模型中，在向极地边缘的地面风是西风循环细胞，向东靠近赤道。这与观察到的模式相似(见图7.28，中间面板)，但不完全相同。事实上，西风带在北纬50°，南纬50°附近最大，显著地向副热带急流的极地方向移动，我们将在第8.4.2节中回到这一点。

如图8.5所示，下沉的亚热带地区是温暖的(因为绝热压缩)和干燥的(因为高空空气比地面空气干燥得多);这种下沉空气与较冷、较湿的近地表空气之间形成的边界是第四章所述的“交换逆温”信风是所在地。在高空，Hadley环流内的水平温度梯度非常弱(见图5.7和5.8)，这是非常高效的结果经向热传输通过循环。

哈德利环流实验:GFD实验室VIII重访

在第八章中揭示了哈德利循环的许多方面，其实验安排已经在图7.12中描述热的风方程。这个装置只是一个圆柱形的容器，里面装着普通的水，中心是一个装满冰的金属罐。随之而来的温度梯度(“向两极”减小)驱动罐内的运动，其性质取决于仪器的旋转速率。当缓慢旋转时，就像在这个实验中(Q < 1转-是的，每分钟只旋转一次桌子:非常慢!)，我们看到热风在流体上部以强烈的“向东”(即超旋转)流动的形式发展，这可以通过漂浮在表面的纸点和注入流体的染料来揭示，如图7.13所示。

实验中观测到的方位角电流，其形成方式与前面讨论过的哈德利环流形成的副热带急流类似，由图7.12(右)所示的经向环流形成的角动量平流维持。水在外层上升，在上层向内移动，保持角动量，从而产生强烈的“西风”流动，与寒冷的内壁摩擦，变冷并下降。高锰酸钾落入流体中的晶体(不要太多!)会落在底部，并显示底部边界层的流动情况。在图8.6中，我们看到流动在底部径向向外移动，并且处于

图8.6。GFD实验室VIII第7.3.1节研究了哈德利政权。底部流动由两条向外螺旋的紫色条纹显示反气旋(顺时针)流动，如图7.12(右)所示;黑色的纸点和绿色的染料领标记上层的流动和循环气旋(逆时针)。

向右偏转，形成与旋转台相反的向东流动;注意两条紫色的飘带向外顺时针移动(与旋转和上层流动的感觉相反)。这种底部气流直接类似于图8.4所描绘的低层大气的偏东信风和向赤道信风，并根据图7.28的观测结果绘制。

实验的定量研究(通过跟踪，例如，漂浮的纸点)表明，上层方位角流动确实保存角动量，非常准确地满足公式6-23，就像在径向流入实验中一样。用Q = 0.1 s-1(对应转速为0.95 rpm;(见表a .1，附录a .4.1)式6-23表明，如果角动量守恒的粒子从外半径t\ = 10厘米移动到内半径10厘米。然而，请注意，如果Q设置为10倍，即10转/分，那么角动量守恒将意味着速度为1m s-1，这是一个非常快的电流。在下一节中，我们将看到，如果我们提高桌子的旋转速度，就不会观察到这样快速的电流。相反，方位电流分解成旋转的运动，引起方位压力梯度，打破角动量守恒。

8.2.2.

尽管图8.5所示的简单Hadley单元模型很好地描述了热带地区，但它预测在中高纬度地区几乎没有发生。在那里，科里奥利参数大得多，旋转的强大约束占主导地位，经向流动受到阻碍。然而，我们期望(并且已经在图5.8和7.20中看到)，在中纬度地区，特别是在亚热带急流附近。因此，虽然没有经向环流，但随着温度梯度，热风平衡存在纬向流动。由于T向极方向减小，式7-24表示西风随高度增加而增加。这种没有经向运动的纬向流状态是完全有效的平衡状态。即使水平温度梯度的存在意味着水平压力梯度(压力面倾斜)，相关的力完全由作用在热风上的科里奥利力平衡，正如我们在第7章中讨论的那样。

我们推断热带以外的平均经向环流较弱，这在定性上与观测结果一致(见图5.21)，但给我们留下了两个问题:

1.向极地的热输送是平衡能量预算所必需的。在热带地区，颠倒的哈德利环流将热量向极地输送，但不会超过亚热带地区。如果没有经向环流，热量如何进一步向极地输送?

2.日常观察告诉我们，把中纬度大气看作纯粹的纬向风是非常错误的。如果这是真的，天气将是非常可预测的(而且非常无聊)。

因此，我们的轴对称模型只是部分正确。对热带以外纯纬向流的预测是完全错误的。正如我们所看到的，中纬度大气中充满了涡流，它们表现为移动的天气系统它们来自哪里?事实上，正如我们现在将通过实验室实验讨论和证明的那样，热带外大气在水动力学上是不稳定的，气流通过一种被称为斜压不稳定的机制自发地分解成涡流这些涡流很容易产生经向运动，正如我们将要看到的，影响热量的经向输送。

斜压不稳定

为了介绍我们通过斜压不稳定来分解热风的讨论，我们描述了这种现象的一个实验室实验。图7.12所示的设备与实验室VIII用于研究热风和哈德利环流的设备相同。在前一个实验中，桌子以Q < 1 rpm的速度旋转得非常慢。然而，这一次，表的旋转速度要快得多，每分钟Q ~ 10转，这代表了在中纬度地区发现的相当大的科里奥利参数。在这种较高的旋转速率下，发生了一些不同寻常的事情。而不是一个稳定的轴对称流，如图8.6所示的Hadley区，建立了一个强涡流流。热风仍然存在，但通过不稳定性分解，如图8.7所示。我们可以看到涡流的发展，在罐体的一个扇区(例如，图8.7中的A)将(相对)温暖的流体从外围扫到冷罐，同时将冷流体从罐带到另一个扇区的外围(例如，图8.7中的B)。这样就实现了径向向内的热量传输，抵消了冰融化造成的中心冷却。

对于图8.7所示的实验，我们观察到水箱周围的三个完整波长。通过重复不同Q值的实验，我们观察到，随着Q值的增加，涡流的规模减小，流动变得越来越不规则。这些涡流的产生机制与图7.20所示的大气天气系统的产生机制相同，稍后将进行讨论。

在继续之前，我们应该强调图8.7中的流动不保存角动量。事实上，如果确实如此，正如第8.2.1节末尾所估计的那样，我们将在冰桶附近观察到非常强的水平流，量级为1m s-1，而不是实验中看到的几cm s-1。当然，这正是公式8-2对大气的描述:如果空气环在从赤道到极点的轴对称运动中保持角动量，那么我们就会得到不现实的大风。角动量不是守恒的，因为存在与涡流运动相关的纬向(或者，在我们的坦克实验中，是方位)压力梯度(见第六章的问题6)。

阿尔伯特·德凡特(Albert Defant, 1884-1974)，德国气象学和海洋学教授，对大气环流理论做出了重要贡献。他是第一个将子午线作类比的人能量转移在亚热带和极地之间由大规模的涡流引起的湍流交换。

在斜压流体中，p = p (p,T)，因此沿着压力面可以有密度梯度(因此也有温度梯度)。这应该与“正压”流体[p = p (p)]形成对比，在“正压”流体中不存在这种梯度。

图8.7。上图:从侧面观察的“涡流”区斜压涡。下:从上面看。在A点，涡流将流体从外围拉向中心，在b点则相反。涡流是由容器中心冰桶的存在引起的径向温度梯度引起的热风不稳定造成的。冰桶的直径为15厘米。

图8.7。上图:从侧面观察的“涡流”区斜压涡。下:从上面看。在A点，涡流将流体从外围拉向中心，在b点则相反。涡流是由容器中心冰桶的存在引起的径向温度梯度引起的热风不稳定造成的。冰桶的直径为15厘米。

中间纬度的天气刚才描述的实验室实验中所研究的斜压不稳定过程是大气中普遍存在的中纬度气流波动的原因。从图5.22、7.4和7.20所示的观测中可以看出，这些波浪经常形成封闭的涡流，特别是在靠近水面的地方，在那里它们被称为与日常天气有关的高压和低压系统。在这一过程中，它们还影响到平衡全球能量平衡所需的向极地的热量输送(见图8.1)。在行星尺度上实现这一目标的方式如图8.8所示。涡流“搅动”大气，将冷空气带到赤道，将暖空气带到极地，从而降低了赤道与极地的温度对比。在图8.8的低空(标记为L)以西，冷空气被带入热带地区。向东，暖空气被带到极点，但由于向极点流动的空气是上升的(记住图5.8中0面的大尺度斜率)，它倾向于离开极点。因此，我们在点1附近得到了一个集中的温度梯度，在这里冷空气“推入”热空气，而在点2处，第二个不太明显的浓度是热空气撞入冷空气。因此，我们可以分别识别冷锋和暖锋，如图8.8的中心面板所示。请注意，用三角形表示“尖锐”冷锋，用半圆形表示“温和”暖锋。 In the bottom panel we present sections through cold fronts and warm fronts respectively.

时间尺度和长度尺度我们已经通过实验室实验证明，热风平衡中的电流可以，而且几乎总是会，变得水动力不稳定，产卵蜿蜒和涡流。更详细的理论分析表明，形成的涡流的横向尺度，例如，

对具有经向温度梯度的热风平衡中最初纬向急流自发产生的不稳定性的空间尺度和增长速率的详细分析表明:

1.扰动进食的就绪增长率由a = 0.31 U/Lp = 0.31 f给出——使用式(7-23)，U = -j-H

(见Gill, 1982)。插入对流层的典型数字，N = 10-2 s-1， = 2 × 10-3 s-1, f = 10-4 s-1，我们发现~ 10-5 s-1, e折叠时间尺度为1天。

2.增长最快的扰动波长为4Lp，其中Lp由式7-23给出。如果Lp = 700千米，则波长为2800千米。地球在北纬45°的周长为21,000公里，因此在任何时候大约可以有7个天气波围绕地球旋转。这与观察结果大致相符;如图5.22所示。

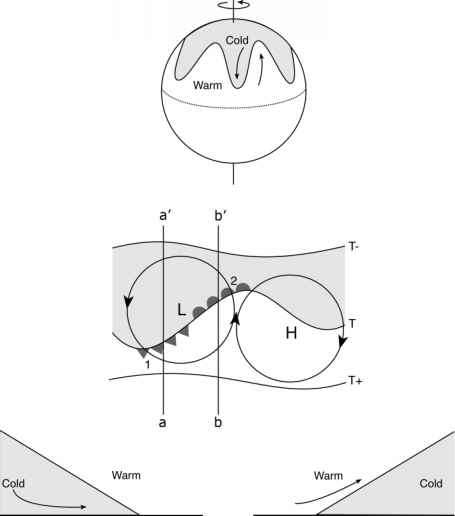
图8.8。上图:在中纬度地区，涡旋将暖空气向极地向上输送，冷空气向赤道向下输送。因此，涡旋倾向于横向“搅动”大气，降低了赤道和极点的温度对比。中图:在“L”的西边，冷空气被带入热带地区。在东方，暖空气被带到极点。所得到的冷锋(用三角形标记)和暖锋(用半圆标记)被表示出来。底部:部分穿过冷锋，一!- > a，暖锋b - > b'。

图8.8。上图:在中纬度地区，涡旋将暖空气向极地向上输送，冷空气向赤道向下输送。因此，涡旋倾向于横向“搅动”大气，降低了赤道和极点的温度对比。中图:在“L”的西边，冷空气被带入热带地区。在东方，暖空气被带到极点。所得到的冷锋(用三角形标记)和暖锋(用半圆标记)被表示出来。底部:部分穿过冷锋，一!- > a，暖锋b - > b'。

如图7.25所示的表面分析中低压系统的典型横向尺度，或在我们的槽实验中看到的染料漩涡，如图8.7)与罗斯比变形半径在第7.3.4节中讨论:

艾迪

其中Lp由式7-23给出。

扰动的时间尺度为:

其中U = du/dz H为上层气流的强度，du/dz为式7-17给出的热风，H为气流的垂直尺度。Eq. 8-4很容易解释为以速度U运动的气流流过Lp的距离所花费的时间，与Eady增长率(倒数)成正比，在Eric Eady7之后，他是斜压不稳定理论的先驱。

在斜压不稳定性实验中，我们估计变形半径约为10厘米，大致与图8.7中观测到的涡旋尺度一致(要确定尺度，请注意图中冰罐的直径为15厘米)。通过跟踪漂浮在流体表面的纸点观察到的典型流动速度约为1cm -1。因此，式8-4表示Teddy ~ 7.0 s的时间尺度，或大约一个旋转周期。与式8-3一致，涡流尺度随转速增加而减小。

将上述公式应用于f ~ 10-4 s-1、N ~ 10-2s-1(见第4.4节)、H ~ 7 km(见第3.3节)和U ~ 10 ms-1的对流层中层，我们发现Lp = NH/f ~ 700 km和Teddy ~ 700 km/10 ms-1 ~ 1 d。这些估计与观测到的天气系统的规模和增长速率大致一致。

斜压失稳机制及其能量来源尚未讨论。为了做到这一点，我们现在考虑流体的能量学和势能的释放。

继续阅读:气候的纬度变化raybet雷竞技最新

这篇文章有用吗?

0 0