信息Gbs

或图6.19局部笛卡尔几何的分量形式，

的地转平衡由式7-2所描述的力的分布如图7.1所示。的压力梯度力当然是从左边的高压系统流向右边的低压系统。平衡科里奥利力必须以相反的方向显示，因此地源平衡流必须垂直于沿定压等高线的压力梯度，如式7-3所示。对于如图7.1所示的北半球情况f> 0)，流动的意义是顺时针围绕一个高压系统，逆时针围绕一个低压系统。(这个意思在南半球是相反的。)这条规则总结在19世纪荷兰气象学家的拜斯-巴洛特定律中:

如果你在北半球背风站着，低压在你的左边

(在南半球是“左”或“右”)。

由式7-3可知地转流取决于压力梯度的大小，而不仅仅是它的方向。

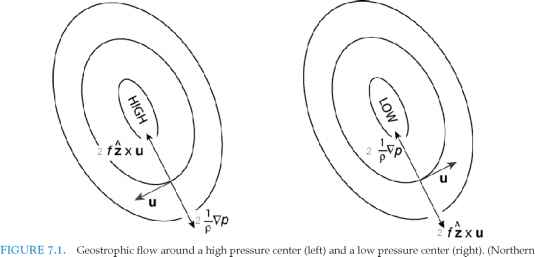
半球壳，f > 0。)科里奥利使流动“向右”偏转的作用(见图6.10)由压力梯度力的水平分量-1/pVp平衡，从高压到低压。

考虑图7.2，其中曲线显示了两条恒压等压线，p和p + Sp，由可变距离Ss分开。从Eq. 7-3, ii 1 ii 1 Sp

1g1fp 1 ^1 fps

由于Sp沿流动是常数，| ug | a (Ss)-1;等压线离得最近的地方气流最强。地转流不穿过压力等值线，因此后者的作用类似于河岸导致河流在窄处流速加快，在宽处流速减慢。这些特征在很大程度上解释了为什么气象学家传统上专注于压力图:压力场决定了风。

注意地转流的垂直分量，如式7-3所定义的，为零。这不能直接从式7-2推导出来，因为式7-2涉及到流动的水平分量。然而，考虑一下不可压缩的流体(在实验室或海洋中)，我们可以忽略p的变化。此外，虽然f在球面上变化，但它在例如1000公里或更小的尺度上几乎是恒定的然后公式7-4给出

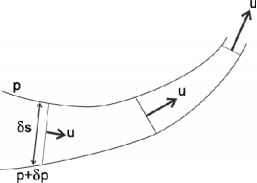
图7.2。水平面上两条压力等值线(等压线)的示意图。地转流，由式7-3定义，是沿着等压线的;等压线越靠近，强度越大。

dxdy

因此地转流是水平不发散的。与连续性式6-11的比较告诉我们dwg/dz = 0;例如，在一个平坦的底部边界上，如果wg = 0，那么到处都是wg = 0，因此地转流确实是水平的。

在可压缩流体中，例如大气，密度的变化使问题复杂化。因此，我们现在考虑在压力坐标下的地转平衡方程，在这种情况下，这种并发症不会出现。

7.1.1.地转风的压力坐标

为了将地转方程应用于大气观测，特别是高空分析(见下文)，我们需要用压力面上的高度梯度来表示它们，而不是像公式7-4中那样，用恒定高度上的压力梯度来表示。

考虑图7.3。该图描述了一个恒定高度z0和一个恒定压力p0的表面，它们相交于a，其中当然压力是pA = p0和z5常数5zq z5常数5zq

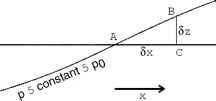
图7.3。用于将高度表面上的压力梯度转换为压力表面上的高度梯度的原理图。

^然而，对于行星尺度的运动，f的变化确实很重要，例如，将在10.2.1节中看到。

高度是za = z0。在高度恒定时，x方向的压力梯度为dp\ = pc - po dx) Sx '。

其中Sx是C和A之间的(小)距离，下标z表示“保持z恒定”。“现在，沿定压面的高度梯度为dz\ = Zb - Zo axjp ~

Sx，下标p表示保持p不变。由于zC = z0, pB = po，我们可以使用流体静力平衡方程Eq. 3写成pc - p0 = pc - Pb = _ dp = zb - z0 = zb - zc ~ dz = gP'

因此，从式7-6中，在y方向上调用类似的结果，可以得出

dX Jz V dX Jp' dp J = V dz J

在压力坐标中，式7-3变成:

其中Zp是压力坐标中的向上单位向量，Vp是压力坐标中的梯度算子。分量形式是，

G dz G dz f dy ' f dx

公式7-8相对于公式7-4的奇妙简化是P没有显式出现，因此，在从观察中评估时，我们不需要关心它的变化。就像常数z表面上的p等高线一样，常数p表面上的z等高线是地转流的流线。如果f为常数，地转风在压力坐标上是不发散的:

Yp ug = dx + dy =0。

公式7-9使我们能够定义一个流函数:

通过代入可以验证，对于任意yg = yg(x,y,p, t)，满足式7-9。将式7-10与式7-8进行比较，我们可以看到:

因此，高度等高线是地转流在压力面上的流线:地转流沿着z等高线，如图7.4所示。

关于风的大小，公式7-8暗示了什么?在图5.13中，我们看到500 mbar压力面在经向距离L = 5000 km上沿高度Az = 800 m向下倾斜;那么地转平衡意味着风速u = g/f Az/L = ff x 5^«15ms-1。

因此，作用在速度为~15ms_1的纬向风上的科里奥利力具有足够的大小来平衡与极有关的向极的压力梯度力赤道的温度梯度。这正是我们所观察到的;见图5.20所示中层流强度。地转平衡因此“连接”了图5.13和图5.20。

现在让我们看一些天气图，如图5.22和7.4所示，看看地转平衡在起作用。

7.1.2.高潮和低谷;综观图表

图7.4显示了500mbar表面的高度(每60米绘制一次等高线)与观测到的风矢量(一个完整的颤振表示风速为10 ms-1)在某一时刻:确切地说，是2003年6月21日格林尼治标准时间12点，与图5.22所示的半球地图时间相同。请注意

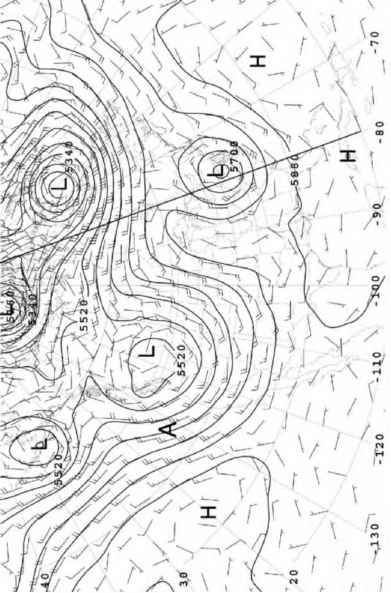
图7.4。500毫巴的风位势高度2003年6月21日格林尼治标准时间12点。[纬度和经度(以度为单位)由图左侧和底部边缘的数字标记。风从箭袋吹开:一个满箭袋表示速度为10毫秒-1，一个半箭袋表示速度为5毫秒-1。地球势高度每60米绘制一次轮廓。高压和低压中心标记为H和l，标记为A的位置用于检查地转平衡。图7.21所示的80°W从20°N延伸到70°N的经向剖面的位置为粗黑线，图7.5、7.20和7.25也标出了这一剖面。

图7.4。2003年6月21日格林尼治标准时间12时的500毫巴风和地球势高度场。[纬度和经度(以度为单位)由图左侧和底部边缘的数字标记。风从箭袋吹开:一个满箭袋表示速度为10毫秒-1，一个半箭袋表示速度为5毫秒-1。地球势高度每60米绘制一次轮廓。高压和低压中心标记为H和l，标记为A的位置用于检查地转平衡。图7.21所示的80°W从20°N延伸到70°N的经向剖面的位置为粗黑线，图7.5、7.20和7.25也标出了这一剖面。

风沿着高度等高线吹，而且等高线越靠近，风就越强。在这个高度，远离地面的摩擦作用，风接近地转风。

例如，考虑图7.4中“A”的左侧“脚”所标记的点，在北纬43°，西经133°。风沿着高度等高线以25 ms-1的速度吹向SSE。我们估计500毫巴高度的地表在250公里内以60米的速度向下倾斜(注意

纬度1°相当于距离111千米，等高线间距为60米)，地转关系式(Eq. 7-7)则表示风速g雷竞技csgo/f Az/L = 981 x " = 24 ms-1，与之接近

观察到。事实上，大气高层的风非常接近地转平衡。

在图7.5中，我们绘制了图7.4所示天气模式的Ro(计算为|u-Vu|/fu|)。在大部分区域大约是0.1，所以气流是

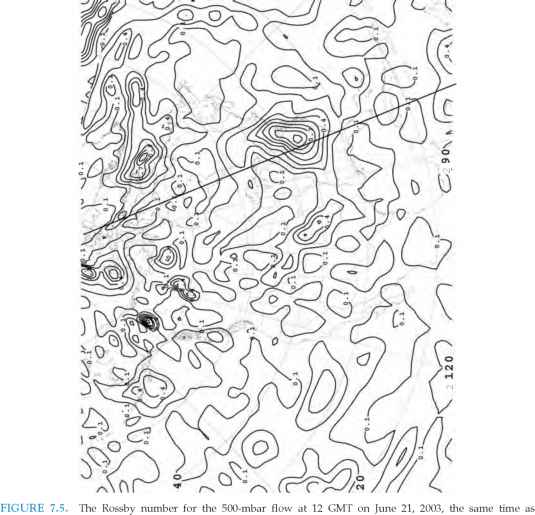
图7.4。等高线间距为0.1。注意，在大部分地区Ro ~ 0.1，但在强气旋中可接近1，如中心在80°W, 40°N的低气压。

在地转平衡中达到很好的近似。然而，在流动强、流动曲率大的强低压系统中，R0可以趋于统一，例如在中心在80°W, 40°n以上的低压系统中，科里奥利项和平流项彼此具有可比性，科里奥利力、内力和压力梯度力之间存在三方平衡。这种平衡称为梯度风平衡(见第7.1.3节)。

7.1.3.径向流入实验中的平衡流动

此时，有必要回到第6.6.1节中描述的径向流入实验GFD Lab III，并假设流体包裹在螺旋进入排水孔时的轴向角动量守恒，计算Rossby数(见图6.6)。式6-23所示的罗斯比数为:

Ro = *VL = i(r2 - i\ (7-12))

r1是容器的外半径。图7.6(右)将其绘制为r/r1的函数。

基于跟踪漂浮在流体表面的颗粒(见图6.6)以及理论预测(公式7-12)观测到的Ro值绘制在图7.6中。我们看到了广泛的一致性，但在小r和高Ro时，观测结果偏离了理论曲线，这可能是因为很难跟踪漩涡高速核心中的粒子(注意图6.6中明显的小半径粒子的模糊)。

由式7-12和图7.6可知，r = r1处R0 = 0，半径为r1/V3 = 0.58r1处R0 = 1，随着r进一步减小R0值迅速增大。因此，在外部区域(小R0)，方位流在地物理上是平衡的，径向压力梯度力平衡了式6-21中的科里奥利力。在内部区域(高R0)，式6-21中的v^/r项平衡径向压力梯度;这就是所谓的循环平衡。在中间区域(其中R0 ~ 1)，式6-21中的三个项都起作用;这就是所谓的梯度风平衡，其中地转平衡和环转平衡是极限情况。如前文所述，在图7.4所示的气候图中，在R0 ~ 1(图7.5)的低压区域，可以看到梯度风平衡。

图7.6。左图:R0数作为无量纲半径(r/r1)的函数绘制，通过跟踪三次径向流入实验(每次以不同的转速，此处引用的单位为每分钟转数[rpm])计算得到。右:基于公式7-12的理论预测。

图7.7。来自GFD实验室0的染料分布:在左边，我们看到染料(红色和绿色)被搅拌到非旋转流体中，其中湍流是三维的;在右边，我们看到染料图案得到的a旋转流体其中湍流发生在垂直于旋转轴的平面上，因此是二维的。

图7.7。来自GFD实验室0的染料分布:在左边，我们看到染料(红色和绿色)被搅拌到非旋转流体中，其中湍流是三维的;在右边我们看到在旋转流体中得到的染料图案，其中湍流发生在垂直于旋转轴的平面上，因此是二维的。

继续阅读:泰勒普罗德曼定理

这篇文章有用吗?

0 0