信息Ntz
假设球,直到被抓住,以一个恒定的向前速度(水平分量)为15米s-1,确定球的横向偏转从直线由于科里奥利效应.[忽略摩擦和任何风或其他空气动力学效应。]
5.想象协和式飞机正以u的速度沿着纬度圈从纽约飞往伦敦。由于科里奥利效应产生的偏转力是向南的。通过稍微降低左翼,飞行员(或者更方便的是机上的计算机)可以平衡这种偏转。画一个力的图-重力,垂直于翅膀的升力,科里奥利力-并用它来推断倾斜角, y,飞机从水平方向平衡所需的科里奥利力为tan y■
其中Q是地球自转,纬度v,重力g。如果u = 600 m s-1,插入典型数字来计算角度。你能用大气环流作什么类比?[提示:参考Eq. 7-8。]
考虑圆形几何中以恒定角速度q绕垂直轴旋转的系统中的水平流动,从式6-29开始,表明该几何中方位角流动的运动方程为,在旋转框架中(忽略摩擦,假设二维流动)。
Dvg Dvg Dvg
Dt Dt dr
(vr, vg)为速度在(r, g) =(径向,方位角)方向上的分量(见图6.8)。[提示:在柱坐标下写出式6-29(见附录A.2.3),注意vr = Dr/Dt;vg = rDg/Dt,梯度算子V = (d/dr,1/r 3/36)]
假设流动是轴对称的(即所有变量都与6无关)。对于这种流动,角动量(相对于惯性系)是守恒的。这意味着,由于单位质量的角动量是
DA _ DA DA = o ~Dt = It + Vr ~3r =。
证明式6-45和式6-47对于轴对称流动是相互一致的。
当水从盆里或浴缸里流下来时,通常会形成漩涡。人们常说,这个旋涡在北半球是逆时针的,在南半球是顺时针的。通过下面的实验来验证这句话。
将一个盆子或浴缸(最好是后者——越大越好)灌满至少10厘米深的水;静置一两分钟,然后沥干水分。当一个漩涡形成时,14尽可能地估计它的角速度、方向和半径(使用小浮子,如铅笔屑,帮助你看到流动)。因此
14可能不会形成清晰的漩涡(中心为“空心”,如图6.7所示)。只要有一个可识别的旋转运动然而,你将能够继续;如果没有,试着重复这个实验。
计算涡旋单位质量的角动量。
现在,假设在你打开排水管的那一刻,没有任何运动(相对于旋转的地球)。如果只有地球自转的垂直分量重要,计算由于地球自转在浴缸或盆的周长引起的角动量密度。[你的浴缸或盆几乎肯定不是圆形的,但假设它是圆形的,其有效半径R使你的浴缸或盆的面积为nR2,以确定m。]
(c)由于角动量应该是守恒的,那么如果在拔塞子的瞬间确实没有任何运动,那么排空涡中单位质量的最大角动量应该与初始时刻周长处的角动量相同(因为周长处角动量最大)。比较你的答案并评论地球自转对排水沟漩涡的重要性。因此,请评论(b)中提到的说法的有效性。
(d)鉴于你对(c)的回答,你对Perrot的实验GFD实验室VI有什么看法?
密度均匀的流体的尺寸、无粘性(F = 0)流动:
这里D/Dt = D/Dt + ud/dx + vd/dy,连续性方程是du dv
dxdy
(a)通过消去两个动量方程之间的压力梯度项,利用连续性方程,证明量(dv/dx - du/dy + f)随运动守恒,从而
D_ / dv_ du \ = 0 Dt\ dx dy +f J =。
(b)确信zv xu dv dx du dy
(见附录a .2.2),即dv/dx - du/dy是一个矢量的垂直分量,称为涡度,vxu,速度场的旋度。
dv/dx - du/dy + f被称为“绝对”涡量,由“相对”涡量(由于相对于旋转行星的运动)和“行星”涡量f组成,由于行星本身的旋转。
通过计算“循环”——u在图6.22所示的x, y平面上矩形元素的线积分,可得:
环流_平均正常面积封闭涡度分量
由此推导出,如果流体元件在固体中旋转,
-
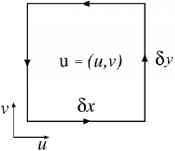
- 图6.22。循环积分示意图。
那么平均涡度等于旋转角速度的两倍。
(d)如果飓风的切向速度变化为v = 106/r ms-1,其中r为半径,计算半径为300 km的内圆和半径为500 km的外圆之间的平均涡量。用单位表达你的答案行星涡度f在北纬20度处的值内圈内的平均涡度是多少?
这一页故意留白
继续阅读:信息Gbs
这篇文章有用吗?
