R

式7-24表示热的风压力坐标中的关系。通过类比式7-8，正如压力面上的高度轮廓作为流线地转流，则由式7-24可知，压力面上的温度等值线充当热风切变的流线。我们顺便指出，在高度坐标中可以得到类似于Eq. 7-24的关系(参见本章末尾的问题9)，但由于Eq. 7-4中的p因子，它就不那么优雅了。热风也可以用势温来表示(见第10题，也在本章末尾)。

经向温度梯度与垂直风的关系

在实际操作中，流体锥在底部摩擦所引起的摩擦会使底部的电流趋近于零。然而，热风切变仍然存在气旋流一直上升到表面。

10在分层流体中，浮力频率(第4.4节)由N2 = -g/p dp/dz或N2 ~ g"/H给出，其中g = g^p/p, Ap是垂直尺度H上密度的典型变化。

式7-24所示的切变在纬向平均气候学中很容易看到(见图5.7和图5.20)。由于温度向极地方向降低，北半球dT/dy < 0，南半球dT/dy> 0;因此f -1öT/öy都< 0。

然后，Eq. 7-24告诉我们du/dp < 0:因此，随着高度的增加(压力减小)，两个半球的风必须越来越东(西风)(如图7.19所示)，这就是我们在图5.20中观察到的情况。

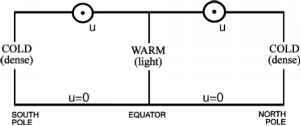
图7.19。在赤道到极点的温度梯度下，在两个半球观测到的西风的热风平衡示意图。(见式7-24，图5.7和图5.20。)

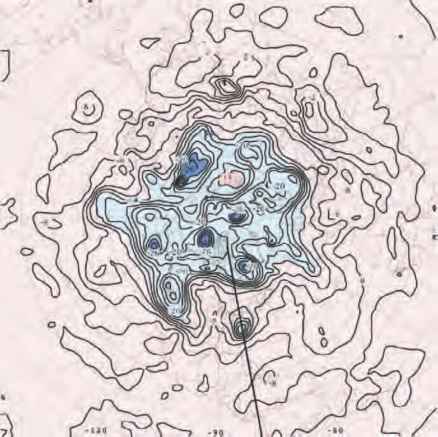
图7.20。2003年6月21日格林尼治标准时间12时500毫巴地表的温度T，与图7.4同期。等高线间距为2℃。粗黑线标出了图7.21所示的80°W从20°N延伸到70°N的经向剖面的位置，一个明显的温度对比区域将暖空气(粉红色)和冷空气(蓝色)分开。北极最冷的温度可低至零下32摄氏度。

图7.20。2003年6月21日格林尼治标准时间12时500毫巴地表的温度T，与图7.4同期。等高线间距为2℃。粗黑线标出了图7.21所示的80°W从20°N延伸到70°N的经向剖面的位置，一个明显的温度对比区域将暖空气(粉红色)和冷空气(蓝色)分开。北极最冷的温度可低至零下32摄氏度。

大气在任何时刻都在大尺度上接近热风平衡。例如，图7.20显示了2003年6月21日格林尼治标准时间12点500mbar面上的T，与图7.4所示的500mbar高度场的曲线时间相同。记住，通过式7-24,T等高线是地转剪切的流线，挖/dp。注意强经向梯度在中纬度与强蜿蜒曲折的急流。这些梯度在图7.21中也很明显，在图7.20中，温度T和纬向风u在80°W穿过大气的垂直横截面，同时从20°N延伸到70°N。纵坐标是压强。注意，根据公式7-24，当T面向上向极点倾斜时，风随着高度的增加而增加，而当T面向下倾斜时，风随着高度的减少而减少。的垂直风切变在T面呈陡坡的区域，强度非常强;垂直风切变在T面几乎水平的地方非常弱。还要注意图7.4中标记的与80°W, 40°N的强低气压相关的异常冷空气。

综上所述，式7-24定量和定性地解释了观测到的大气中水平温度梯度和垂直风切变之间的联系。正如我们将在第九章中看到的，热风的类似表达也适用于海洋。

沿80 W风向和温度的瞬时剖面

图7.21。2003年6月21日，格林尼治标准时间12点，纬向风u(颜色刻度，绿色表示远离我们，棕色表示向我们，每5毫秒-1一次薄等高线)和温度T(每5°C一次厚等高线)穿过80°W的大气，从20°N延伸到70°N，如图7.20和7.4所示。注意在dT/dy < 0的区域du/dp < 0，反之亦然。

图7.21。2003年6月21日，格林尼治标准时间12点，纬向风u(颜色刻度，绿色表示远离我们，棕色表示向我们，每5毫秒-1一次薄等高线)和温度T(每5°C一次厚等高线)穿过80°W的大气，从20°N延伸到70°N，如图7.20和7.4所示。注意在dT/dy < 0的区域du/dp < 0，反之亦然。

7.4.亚地转流埃克曼层

在回到我们在第8章中讨论的大气环流之前，我们必须进一步发展一个动力学的思想。尽管自由大气和海洋中的大尺度流动接近地转风平衡和热风平衡，但在流体在固体边界上摩擦或风直接驱动海洋的边界层中，我们观察到由于公式6-29中摩擦项的存在而明显偏离地转风平衡。

的动量平衡如果流动足够慢(Ro << 1)且摩擦力F足够小，则可以忽略式6-43中的F和Du/Dt。摩擦效应在大气和海洋内部确实很小，但在边界层中却变得很重要。在大气底部一公里左右的地方，表面的粗糙度产生了湍流，它将较低边界的阻力传递给了上面的自由大气。在海洋顶部100米左右的地方，风会产生乱流，把风的动量带到海洋内部。F变得重要的层叫做埃克曼层，埃克曼是以瑞典著名的海洋学家埃克曼命名的。埃克曼研究海洋中的风漂移，我们将在第十章详细讨论。

如果再次假设罗斯比数很小，但F现在不可忽略，则动量平衡的水平分量(式6-43)为:

为了可视化这些平衡，请考虑图7.22。让我们从u开始:单位质量的科里奥利力，- fzxu，必须在气流的右边，如图所示。如果单位质量的摩擦力F作为“阻力”，它将与主流气流相反。这两个力的和是

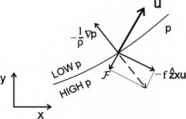
图7.22。公式7-25中的力的平衡:虚线是矢量和F-fz x u，由-1/pVp平衡。

由虚线箭头描绘。这必须通过压力梯度力单位质量，如图所示。因此压力梯度不再垂直于风矢量，或者说，风不再沿着等压线方向。尽管流的左侧仍有低压的趋势，但现在有一个(摩擦诱导的)压力梯度向下(向低压方向)的成分。

由此可见，在F存在的情况下，流动速度为亚地转(小于地转)，因此科里奥利力(其大小与速度成正比)不足以平衡压力梯度力。因此，压力梯度力“获胜”，导致从高压到低压的地转成分。气流沿压力梯度轻微“下降”。

明确地转和地转成分中的水平流uh是有用的，如下所示:

其中uag为地转流，即实际水平流与地转值ug的偏离，如式7-3所示。利用式7-25、式7-26和地转关系式7-2，我们可以看到:

继续阅读:了解观测到的环流

这篇文章有用吗?

0 0