地表风应力Nm2

Lcr.jlturtc

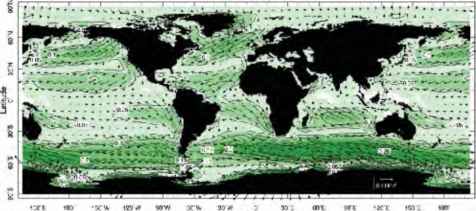
图10.2。海洋年平均风应力。绿色阴影和轮廓表示压力的大小。应力值为0.1 ~ 0.2 Nm-2中纬度西风带，在南半球尤其强烈。箭头是长度为0.1 Nm-2的矢量。注意，应力矢量在图7.27所示的高低压中心周围循环，如果应力所依赖的地表风具有强烈的地转成分，那么人们就可以预期到这一点。

Lcr.jlturtc

图10.2。海洋年平均风应力。绿色阴影和轮廓表示压力的大小。中纬度西风带以下的应力值为0.1 ~ 0.2 Nm-2，南半球的应力尤其强。箭头是长度为0.1 Nm-2的矢量。注意，应力矢量在图7.27所示的高低压中心周围循环，如果应力所依赖的地表风具有强烈的地转成分，那么人们就可以预期到这一点。

10.1.1.力量和运输的平衡埃克曼层

如果罗斯比数很小，我们可以忽略水平动量方程9-7中的D/Dt项，将它们简化为科里奥利力、水平压力梯度和施加的风应力强迫之间的三方平衡。这就是公式7-25，其中F被解释为由于风作用于海洋而施加的物体力。首先，我们需要用风应力(Twind)表示F。

如图10.3所示，应力随深度的变化而变化，作用在一个海洋体上。这里感兴趣的应力分量，tx (z)，是作用在深度z处的力的x分量，每单位水平面积在下面的层上。注意t的单位是Nm-2。在z层的厚度为Sz的平板在其上表面受到每单位水平面积tx (z + Sz)的力，但它下面的层也受到每单位水平面积tx (z)的力。因此，该层感受到的单位水平面积的净力为tx(z + Sz) - tx(z)。由于平板的厚度为Sz，所以它每单位水平面积的体积为Sz;如果板的密度是均匀的，那么

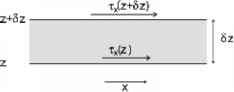
图10.3。假定施加在深度为Sz的流体元素板上的应力随深度而减小。

每单位水平面积的质量pref Sz。因此，平板感受到的单位质量的力Fx为

单位面积上的力，单位面积上的质量

适用于小板厚。我们可以得到Fy的类似关系，因此可以写成:

对于水平应力向量t = (tx,tv)。因此，稳态循环的动量方程变成了公式7-25

上面定义的F，为了方便，我们把它写成分量形式:

公式10-3描述了直接由风驱动的环流中的力的平衡，但它还没有告诉我们这个环流是什么。表面的应力是已知的，即图10.2所示的风应力，Twind，但我们不知道表面下应力的垂直分布。风应力将通过局限于海洋近表层的湍流、风搅动运动向下传递。风强迫的直接影响随深度而衰减(相当快，在几十米左右，取决于风力强度)，因此当深度z = -5时，应力已经消失，t = 0，如图10.4所示。如第7章所述，这是Ekman层。

方便的是，我们可以绕过需要知道t的详细垂直分布，通过对层进行垂直积分来关注层的传输属性。如第7.4节所述，我们将流分为地转和地转两部分。由式10-2给出F，式7-25的地转成分为

将Eq. 10-4乘以pf，从t = Twind的表面到深度z = -5，其中t = 0(见图10.4)，对整个层进行积分，得到:

继续阅读:首选dX f dy f

这篇文章有用吗?

0 0