热风方程

我们在5.2节中看到等压面从赤道向下倾斜到极点。此外，这些斜率随着高度的增加而增加，如图5.13所示原理图，图5.14。因此，根据地转关系，式7-8地转流将随着高度的增加而增加，如图5.20所示。而根据T-P, dug/dz = 0。这是怎么呢

的Taylor-Proudman定理属于一种缓慢、稳定、无摩擦的正压流体，其中p = p(p)。但是在大气中海洋,密度确实在压力表面上有所变化，因此T-P并不严格适用，必须修改以允许密度变化。

让我们再次考虑旋转容器中的水，但现在假设水的密度变化如下:

Pref，其中prff是一个恒定的参考密度，a，称为密度异常，

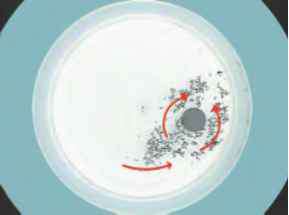
图7.11。图7.10所示实验中流体表面的纸点。在图7.9所示的示意图的实验确认中，这些点围绕着一个淹没的障碍物移动，但没有移动到上面。

密度的变化是关于这个参考。8吗

现在，利用方程3-3的流体静力关系，计算方程7-4的d/dz(将p替换为分母中出现的pref)，我们得到:

du符号(见附录)

如果p在水平方向上变化，那么地转流会在垂直方向上变化。用温度来表示事物，从而推导出一种联系(称为温度)热的风方程)之间的电流和热场，我们可以使用我们的简化状态方程的水，方程4-4，假设水的密度与温度T呈线性关系。则式7-17为:

式中a为热膨胀系数。这是将地转流的垂直切变与水平温度梯度联系起来的热风关系的简单形式。它只告诉我们流体静力平衡和地转平衡，公式3-3和公式7-4，但它以不同的方式表达这些平衡。

我们看到dug/dz和T之间的关系与ug和p之间的关系完全类似(比较公式7-18和7-3)。所以如果我们有水平的温度梯度地转流就会随高度而变化。西风随着高度的增加而增加，因为通过热风关系，西风与向极方向有关温度下降．我们现在在实验室里继续研究热风，在实验室里，我们把一个冰桶放在一个旋转的水箱的中心，代表冷极。

7.3.1.GFD实验室VIII:热风关系

得到由驱动的稳定的轴对称循环是很简单的

8通常情况下，在旋转水槽实验中，海水的密度也一样(见9.1.3节)，其参考值的变化只有百分之几。因此a/pref确实很小。

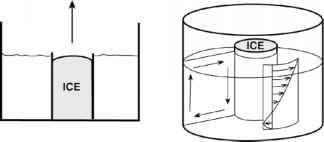
图7.12。我们把一个圆柱形的罐子放在一个转盘上，转盘的中心是一个罐子，在罐子里装满水到10厘米左右的深度，然后非常缓慢地旋转转盘(1转或更少)。在实现固体旋转后，我们用冰/水装满罐子。中间的冰罐引起了径向温度梯度。一个热风切变与它平衡发展，可以用染料可视化，如图所示。实验时间为5分钟左右，以便循环发展。通过温度计监测径向温度梯度，通过跟踪漂浮在表面的纸点测量电流。

图7.12。我们把一个圆柱形的罐子放在一个转盘上，转盘的中心是一个罐子，在罐子里装满水到10厘米左右的深度，然后非常缓慢地旋转转盘(1转或更少)。在实现固体旋转后，我们用冰/水装满罐子。中间的冰罐引起了径向温度梯度。一个热风切变与它平衡发展，可以用染料可视化，如图所示。实验时间为5分钟左右，以便循环发展。通过温度计监测径向温度梯度，通过跟踪漂浮在表面的纸点测量电流。

图7.13。在热风平衡的方位角电流作用下，染料条纹倾斜成螺旋状，中心的冰桶保持径向温度梯度。

本实验室水箱内的径向温度梯度，为研究热风关系提供了理想的机会。

该装置如图7.12所示，如图7.13所示。圆柱形容器的中心是一个冰桶，它非常缓慢地逆时针旋转。冷侧可以冷却邻近的水，并产生径向温度梯度。纸点洒在表面上的运动与旋转桌子的运动具有相同的意义，但比旋转桌子更快——我们产生了西风(向东)流!我们注入一些染料。染料条纹不是垂直的，而是在一个方位方向上倾斜，由随着高度而增强的电流携带，其方向与旋转工作台的方向相同(见图7.13中的照片和图7.14中的示意图)。泰勒柱被西风吹倒了。

对于柱形几何中的不可压缩流体(见附录A.2.3)，热风关系的方位角分量，方程7-18为:

其中vg为方位电流(参见图6.8)，f已被2Q取代。由于T从冷中心向外移动时增加(dT/dr > 0)，那么对于正Q, dvg/dz> 0。由于vg在罐底受到摩擦力的限制是较弱的，因此我们期望在顶部看到vg > 0，在最大密度梯度半径处流动最强。图7.13中可见的染料条纹清楚地显示了热风切变，特别是在冷罐附近，那里的密度梯度很强。

我们注意到内外壁之间距离L的温差AT(每10厘米为1°C)，以及纸点相对于容器表面的速度(通常为1厘米s-1)。的

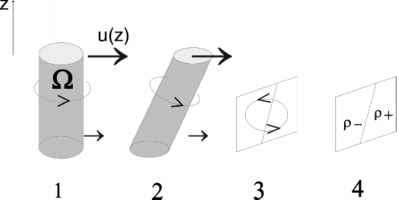
图7.14。显示热能物理含量的示意图风方程写成式7-20:旋转矢量2Q[1]相关的自旋被垂直剪切(du/dz)[2]倾斜。横切面的循环发展[3]，从稳定的垂直梯度产生水平密度梯度。作用在倾斜密度面上的重力平衡了与倾斜泰勒柱[4]相关的倾覆力矩。

图7.14。示热风方程物理内容的示意图，形式为Eq. 7-20:与旋转矢量2Q[1]相关的自旋被垂直切变(du/dz)[2]倾斜。横切面的循环发展[3]，从稳定的垂直梯度产生水平密度梯度。作用在倾斜密度面上的重力平衡了与倾斜泰勒柱[4]相关的倾覆力矩。

水箱以1转/分的速度转动，水深H ~ 10厘米。由上述热风方程，我们估计出ag AT -i ug ~——H ~ 1cms 1，

a = 2 × 10-4 K-1，大致如我们所观察到的。

本实验将在第8.2.1节中进一步讨论，作为一个简单的热带模拟哈德利环流大气的。

7.3.2.热风方程和泰勒-普罗德曼定理

T-P定理和热风方程之间的联系可以通过注意等式7-17和7-18是我们现在推导的热风方程的更一般陈述的简化形式来更好地理解。

取Vx (Eq. 7-13)，但现在放宽正压流体的假设，我们得到[注意到Eq. 7-13左侧项的变换与Eq. 7-14的推导相同，并且Vx (1/pVp) = 1/p2Vp xVp = 1/p2Vp xVp]:

继续阅读:R

这篇文章有用吗?

0 0