角动量变化与地球自转
大气质量的分布及其变化的运动已为人所知相当长一段时间。纬向环流的基本结构,即西风带中纬度地区有风而且东风在低纬度和高纬度地区,在19世纪得到了很好的评价,经向环流也是如此,其特点是直接哈德利环流热带地区上升的空气和进一步向极地下降的空气。当确定中纬度的平均单元是间接的时,更多的结构被注意到套圈细胞,都是间接的。纬向平均运动和涡旋运动都负责向子午输送动量。利用探空仪网络,对这些大型环流系统的年际和年际信号进行了综合;Peixoto和Oort(1992)对此作了总结,尽管他们只处理了轴向分量大气角动量.从各种业务气象序列和再分析中也得到了类似的结果。
值得注意的是,大气的整体大气角动量(AAM)发生了显著的变化,特别是随着季节的变化。在北半球冬季和夏季之间,AAM的相对变化为两倍,冬季半球急流水平的强烈冬季风尤其强烈。而西风,由于两半球副热带和中纬度近200 hPa急流的极大值携带了大部分轴向AAM,因此年际、季节和季节内尺度的变化分布有所不同。对于ISV, Rosen和Salstein(1983)指出,它们更均匀地分布在半球的低纬度地区。
早期出现了一个重要的问题,即AAM的变化如何发生得如此迅速和显著。从物理上讲,系统中的角动量只能通过施加在该元素上的力矩来改变,因此对陆地AAM扭矩的搜索导致了两种特殊的机制:一种是来自对地形的法向压力,另一种是来自沿边界的切向摩擦。我们将在本章后面讨论这些力矩及其含义。特别是对于ISV,已经对这种时间尺度上的角动量-扭矩进行了详细的研究,并与其他元素相关。Lau et al.(1989)和Kang and Lau(1990)考虑了已知的isv如何影响全球角动量的因素,其贡献确实在对流层上部达到峰值,他们将这种变化与加热、动力学和对流的影响联系起来,特别是在热带太平洋上空,伴随着角动量在海洋边界的摩擦力矩转移。随着角动量以地球自转的形式从大气转移到固体地球,理解其旋转变异性的概念以及如何测量它是很重要的。
如上所述,连接所谓的地球和天体参考系的地球自转,只是地球的均匀每日旋转加上一些非常微小的变化。与三维世界中的任何旋转一样,地球的旋转可以用三维矢量表示。(注意,在ra-D空间中旋转向量的张量维数是n(n - 1)/2。)因此,地球自转与空间均匀旋转的偏离可以方便地分为两部分:(i)沿平均旋转z轴的(1-D)轴向分量的大小,它穿过平均南北两极的表面,决定了日长变化(ALOD);和(ii) x-y平面上的(二维)赤道分量,给出地球上看到的旋转轴的方向,称为极运动。
SLR和VLBI,以及最近的GPS,一直是测量地球自转的主要技术。如Gross et al. (1998a)所述,我们在这里使用的数据集是这些技术的最佳组合。亚毫弧秒精度(1毫弧秒,或mas,如果投影到地球表面,大约相当于3厘米)现在在准日常测量中通常可以实现。
8.2.1日长变化与轴向角动量
如上所述,地球自转的变化是地球物理流体角动量变化的结果。其中,AAM是大气环流系统中一个基本而重要的量;除了与大气层内部的交换外,其总量也在不断变化,因此角动量被转移到固体地球和从固体地球转移出去,改变了(固体)地球的旋转。让我们首先关注(1-D)轴分量-平衡的大气一侧的AAMz和大地一侧的ALOD,其中z轴是连接平均南北极的轴。(完整LOD变化的现代视角可以在,例如,Chao, 2003中找到。)蒙克和麦克唐纳(1960)的重要工作中明确提出了计算AAM(或地球物理流体中由于质量传输引起的任何角动量)的公式,后来巴恩斯等人(1983)和尤班克斯(1993)将其更新为越来越合适的地球参数。
一般来说,地球物理流体的质量在运动时产生角动量变化,角动量变化由两部分组成——一部分是由于该质量相对于地球的实际运动,另一部分是由于质量重新分配导致的惯性张量变化(与行星一起参与其固体旋转)。对于AAM的轴向z分量,我们有,大约:
AAMz的运动项(或“风项”)=-
Cwg我
AAMz的质量项(或“压力项”)
从物理上看,(8.1a)类似于伐木工人在水面上“奔跑”(并保持平衡)时,漂浮在水上的圆木所发生的情况;(8.1b)类似于旋转滑冰运动员的现象——当滑冰运动员将手臂靠近身体时,她的旋转速度会加快,而当她将手臂靠近身体时,她的旋转速度会减慢。
方程中u和p分别为(纬向)西风场和地面压力场;a、w、g分别为地球的平均半径、平均转速、平均重力加速度;Q是
(0, A) =(纬度,经度),其中dQ = cos 0 d0 dA是曲面元素。dp可以通过流体静力关系dp = -pg dh转换为垂直距离元素dh,其中p为空气密度。(8.1a)和(8.1b)前面的乘法系数说明了一些微妙但重要的影响,包括地球的弹性屈服表面负荷.C为地幔平均轴向转动惯量;在C中,地核被排除在外,因为在ISV时间尺度上,地核不参与地幔的旋转变化几乎是正确的(例如,Barnes et al., 1983)。换句话说,我们假设在这样的时间尺度上,核幔耦合强度为零,这些时间尺度比十年尺度短得多,而与核幔耦合相关的时间尺度更长。请注意,为了简单起见,我们已经将AAM术语与地球参数标准化,因此它们是相对于平均太阳日长度86,400秒的无量纲“激发”单位。AAMZ导致的LOD变化为:
AAMZ (sum of 8.1a + 8.1b) = -ALOD /LOD。(8.2)
注意,AAMZ的增加减慢了行星的旋转速度,导致LOD增加。在绝对单位中,1毫秒(ms)的ALOD变化相当于地球方向上的15毫弧秒(mas)或地球表面上的~ 45厘米,在这段时间内所对应的旋转角度和距离,这反过来对应于5.95 x 1025kgm2s-1的AAM转移。
当然,并非所有LOD的变化都来自AAMZ(例如,Chao, 2003)。在ALOD数据中,特定时期的潮汐信号并不符合关系(8.2),因为它们是外部月球和太阳扭矩以及由此产生的内部相互作用的结果(这本身就是一组非常复杂的现象)。例如,ALOD中的长周期潮汐信号(如两周和每月的潮汐)来自固体地球潮汐变形,海洋潮汐在较小程度上是造成日和半日ALOD的主要原因。对于季节性(每年+半年)信号,尽管它们的大多数与AAM有关。相当一部分来自潮汐和非大气质量输送。海洋角动量和陆地水文角动量是后者的例子,它们各自有类似于(8.1)的表达式。LOD也有一个大的,缓慢的(十年)波动,主要是由核心角动量变化造成的,以及由于“潮汐制动”导致的LOD的长期增加,月球通过潮汐能量耗散减慢了地球的旋转,而两个天体之间的距离增加了——这是自19世纪乔治达尔文以来长期讨论的现象(例如,Cartwright, 1999);这里也不讨论这些问题。
需要指出的是,AAM质量项的评估受到一个与海洋行为有关的重要不确定性的影响,即反转气压计(IB)假设。IB假设规定,世界海洋的高度会随着上覆大气压力的变化而瞬间均衡地调整。动态地说,净效应是海洋只是在整个海洋区域上均匀地抹去了大气压力的变化。理想状态是对现实的一个很好的近似,特别是在超过十天左右的时间尺度上,例如ISV, IB效应导致显著降低
大气角动量和l.o.d(去掉平均值)
大气角动量和l.o.d(去掉平均值)
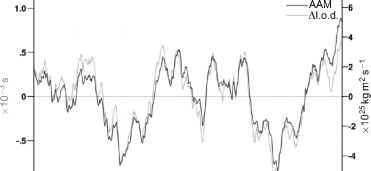
图8.1。由NCEP-NCAR计算的大气AAMZ轴向角动量(黑色)。再分析,与LOD(灰色)相比,从一个组合大地测量解,在等效单位2年。大气激励AAMZ是假设海洋具有IB效应的风项和压力项之和。平均值已被删除。注意这两个系列非常一致;这些差异表明非大气对ALOD的贡献。除了季节性特征,一个非常突出的ISV是值得注意的。
2000
2001
图8.1。由NCEP-NCAR计算的大气AAMZ轴向角动量(黑色)。再分析,与LOD(灰色)相比,从一个组合大地测量解,在等效单位2年。大气激励AAMZ是假设海洋具有IB效应的风项和压力项之和。平均值已被删除。注意这两个系列非常一致;这些差异表明非大气对ALOD的贡献。除了季节性特征,一个非常突出的ISV是值得注意的。
在质量(压力)项的可变性的ALOD,并就此而言,极地运动,时变重力,和geocenter运动。
关于AAMZALOD关系的第一个详细结果是Hide等人(1980)和Langley等人(1981)的结果。这两个量之间的线性关系后来被Rosen和Salstein(1983)以及随后20年的一些后续调查所证实,这些调查基于逐步改进的AAM估计和LOD观测,令人欣慰的是,这导致了它们之间的相关性不断提高(例如,Eubanks, 1993;迪基,1993)。从年际、季节内到短至几天的大范围时间尺度上观察到线性关系(Rosen et al., 1990;Dickey等人,1992),接近现代LOD数据的极限分辨率。
因此,一旦获得高质量的高时间分辨率数据,在几天到几年的时间尺度范围内,纬向大气环流系统与ALOD之间的密切关系就变得非常明显(图8.1)。这是由于以下事实:(i)在所有贡献来源中,数天至年际的ALOD以AAMZ为主;(ii)纬向m风场决定的运动项对AAMZ的贡献(8.1a);(iii)纬向m风是大气环流场的主要特征;(iv)质量项(8.1b)贡献相对较小,因此其对“IB与非IB”的不确定性只是次要影响。然而,类似的密切关系很难在其他大地观测资料中建立起来,例如极地运动、时变重力或地心运动——事实证明,这些对应的关系更加难以捉摸,后来只有通过更好的观测、分析和改进大气模型才能实现。
今天,AAMZ在天气预报中心,如美国国家环境预报中心(NCEP)和欧洲中期天气预报中心(ECMWF),通常以6小时为间隔,使用各自的大气分析结果,按照(8.1)进行常规计算。质量项以两种方式计算:有IB假设和没有IB假设。这些数据集可从国际地球自转和参考系统服务的全球地球物理流体中心大气特别局获得(Salstein et al., 1993,2001;Chao等人,2000)。图8.1给出了一个例子,显示了ALOD和AAMZ之间的2年跨度非常一致,包括季节特征和明显强烈的同期季节内变化。再一次,小的差异表明存在非aam对ALOD的贡献,假设数据集中有小的误差。事实上,这些剩余的信号与海洋角动量的变化有关(例如,Marcus等人,1998;Johnson et al., 1999)。
Langley等人(1981)专门研究了ALOD的近50天(ISV)振荡,使其与AAMZ的联系可能与Madden-Julian振荡(MJO;Madden和Julian, 1971, 1972)和LOD变异性的发现具有相似的时间尺度(Feissel和Gambis, 1980)。此后,对AAMZ和ALOD中的ISV进行了一系列研究,特别是Anderson和Rosen(1983)将振荡与太平洋中部的对流联系起来,Weikmann和Sardeshmukh (1994), Weickmann等人(1997)将研究范围扩大到印度洋的活动,并将角动量动力学与太平洋上的波列联系起来。事实上,即使是季节内振荡的限制热带地区有人提出质疑,认为存在独立的热带外振荡的角动量特征(Dickey等人,1991)。Lau et al.(1989)用热带ISV模态研究了AAMZ与出射长波辐射(OLR)的关系。Gutzler和Ponte(1990)研究了热带纬向风、近赤道海平面、AAMZ和ALOD之间的相干性,它们都表现出包括MJO在内的广泛的ISV。Rosen等人(1991)根据频带和地理带将AAMZ的变异性分开,并特别发现ISV主要来自热带和亚热带的行为。Itoh(1994)进一步指定亚热带为AAMZ ISV的来源区域。Hendon(1995)证实LOD的50天峰值与MJO的活跃期有关。Marcus et al.(2001)报道了AAMZ和ALOD的ISV与El Nino Southern Oscillation (ENSO)的相关性,但MJO与ENSO之间缺乏直接关系。
为了更全面的诊断分析,揭示不同频率信号强度的时间依赖性,我们可以使用时频小波谱分解时间序列。这种特殊的技术基本上显示了
频谱功率的“轮廓线”,使用给定形状的运行短波包(“小波”)在给定(短)时间段内挑选出任何给定(窄)频带内的功率(c.f., Chao和Naito, 1995)。当然,这样的频谱在频率和时间上的分辨率都是有限的,但它们可以有效地概述具有宽带频谱内容的时间序列。因此,在具有不同频率-时间特征的ISV信号的情况下,人们将能够看到它的完整演变。
为了产生ALOD时间序列的小波谱(图8.2,上面板),通过减去最小二乘拟合提前去除最强信号,即季节性项(年度和半年),以揭示其他感兴趣的信号。虽然不是这里讨论的主题,但清楚地看到的是长周期的潮汐项(主要是两周一次的My在13.66天,每月的Mm在27.55天,与月球潮汐相关的18.6年周期调制岁差周期,以及预期的半年潮汐期)。这里我们只画实部(小波变换的余弦项),以便显示波动的正负极性。值得注意的是,最强烈的ISV信号(例如,在2001-2002年左右,出现在记录的最后一部分的最强亚季节信号)所表现出的长时间的年代际尺度波动。相比之下,图8.2(下面板)(见颜色部分)显示了计算出的非季节性AAMz。仔细检查两个光谱的ISV部分,发现非常好的一致性,证实了时域比较中的明显特征(图8.1)。同样明显的是年际波段的一致性,表明年际ALOD是由与重要ENSO和QBO(准双年振荡)信号相关的AAMz(主要在u型风场)变化引起的(例如,Chao, 1989);1980-1985年和1995-2000年交替出现的迹象就是这样的例子。
8.2.2极运动激发和赤道角动量
接下来,我们将研究二维赤道x-y分量——大气一侧的aamxy(在与AAMz正交的赤道平面上)和大地测量一侧的极运动(地球的旋转摆动)。由于一些天文和地球物理过程,地球旋转轴指向的方向(靠近平均极点)会发生变化。当从太空观察这些绝对变化时,类似于旋转(和旋转)顶部的绝对变化,被称为章动(包括我们熟悉的天文岁差)。另一方面,极运动是同一旋转轴方向,但相对于坐在地球上的观察者,因此与地球参考系旋转。即使整个行星的绝对动量是守恒的,观测者也能看到极运动。类似于这种运动的是一个扔得不好的、摇摇晃晃的飞盘。这里与我们相关的重要事实是,与章动放大外部天文影响相反,极移放大了内部地球物理影响,例如地球物理流体之间的角动量交换。
与由大气纬向风场主导的z分量不同,大气动力学的x-y分量具有更微妙的相互作用,它们受到大气科学家的较少关注,尽管在理想化的大气模型中已经注意到了引起极运动的模态(Feldstein, 2003)。对应于(8.1),(归一化的,无维的)AAM的x-y分量的表达式约为(Munk and MacDonald, 1960;巴恩斯等人,1983):
AAM运动项
AAM的质量项
(C - A) gpcos9sin9eix dQ (8.3b)
式中C为(8.1)中地幔的主惯性动量,A为地幔指向赤道平面的平均惯性矩。
注意,现在运动项包括v,子午风场,以及u。对于极运动激发,压力项主导风项。这一项是由球谐波中的(次= 2,阶= 1)项产生的,该项有利于1号纬向波,以及在每个半球的两个中纬度地区具有最大振幅和相反相位的波。这种不均匀的质量分布,无论是在纬度还是经度上,都在地球的相反部分引起了质量的不平衡,这是对极运动的激励。在我们的旋转滑冰运动员的类比中,如果她以不对称的方式收缩她的两只手臂(例如,一只手臂高于另一只手臂),她会在继续旋转时摇摆。赤道和两极(北纬0°、90°和南纬90°)附近的载荷不会像这些那样产生极移纬度是(2,1)激励项的节点;因此,全球范围内强烈的ISV需要出现在中纬度地区,才能对极移产生明显的影响。
与(8.1)相反,这里轴向和赤道转动惯量之间的差,C - A,开始发挥作用。相对差(C - A)/C,约300分之一,代表地球的扁率,这反过来是地球自转的结果。它是稳定因素,保持极运动在检查和防止地球的轴比如说,经历了一次灾难性的暴跌。事实上,经过一个与地球弹性以及地核和海洋的参与/不参与有关的因素修正后,它导致了地球的共振振荡,即钱德勒摆动,自然周期为pc = 434天。作为一种阻尼振荡器,钱德勒摆动也有一个自然阻尼因子,或质量因子Qc,估计高于50(例如,Furuya和Chao, 1996)。
观测到的极移是一个相对较大的绕标称北极的旋转轴的前进运动(如果从北极上方观察,则为逆时针),其振幅为几米,主要由强迫的年度摆动和兴奋的钱德勒摆动组成。AAMxy与其激发极运动P(以弧度表示)的运动方程为:
AAMxy (sum of 8.3a + 8.3b) = P - - - P (8.4)
激发极运动,亚季节带
激发极运动,亚季节带
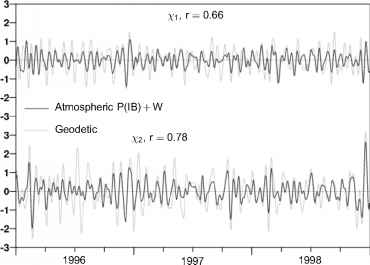
图8.3。极运动激励函数的比较:黑色是由ncap - ncar再分析系统计算的赤道AAMj7,灰色是由自由钱德勒共振大地测量观测到的极运动数据的反褶积,用于x和y分量。大气激励AAMxy是假设海洋具有IB效应的风项和压力项之和。单位为x 1(T7弧度(1弧度= 2.06 x 108mas)。在这里,该系列在ISV波段中进行滤波,并在该时间尺度上具有相对较好的相位关系。表示相关系数r。
图8.3。极运动激励函数的比较:黑色是由ncap - ncar再分析系统计算的赤道AAMj7,灰色是由自由钱德勒共振大地测量观测到的极运动数据的反褶积,用于x和y分量。大气激励AAMxy是假设海洋具有IB效应的风项和压力项之和。单位为x 1(T7弧度(1弧度= 2.06 x 108mas)。在这里,该系列在ISV波段中进行滤波,并在该时间尺度上具有相对较好的相位关系。表示相关系数r。
其中钱德勒频率uc = 2^(1 + i/2Qc)/pc,给出一个复数来考虑阻尼。在(8.3)和式(8.4)中,实部和虚部分别表示沿格林威治子午线的x分量和沿东经90°的y分量。
式(8.4)描述了一个受激的二维线性共振系统,其左边的激励函数为AAMxy。求解时,极运动P是极运动激励函数AAMxy与地球共振为自由钱德勒摆动的时间卷积。相反,(8.4)的右边运算表示观测到的极运动P从自由钱德勒摆动的反褶积。结果,通常表示为%-函数(见图8.3),然后是观测到的极运动的激发。它包括一个宽带信号(包括ISV),加上强烈的季节性(每年+半年)项,主要是由大气产生的,以及长期的长期漂移,主要是由于自1万年前最后一个冰期以来,冰盖卸载导致固体地球在冰期后反弹。因此x中的宽带信号与非季节性的AAMxy直接比较。
图8.3显示了在选定的几年中,ISV波段中这种极运动激励的比较;这里我们删除了季节性和长期术语,类似于早期的ALOD示例,因为它们在时间范围内我们目前的利益。再一次,很好的一致性是显而易见的;广义isv波段相关系数x分量高达0.66,y分量高达0.78。
Eubanks等人(1988年)首先报道了这种相关性,然后是其他一些研究。然而,可以注意到,这种一致性并不像ALOD的轴向情况那样好。这种差异与不同的物理机制有关。例如,与ALOD不同,质量(压力)项比运动(风)项的贡献更大,因此IB效应减少了有效表面压力激励,在评估AAMxy时引入了更大的不确定性。在轴向情况下,主要受到西风的强迫,大气的主要纬向环流强烈地投射到ALOD的激发上。对于大气和大地极运动信号的一致性,不考虑IB时,气象信号的振幅大于大地极运动信号的振幅,而考虑IB时,气象信号的振幅太小(如图8.3所示);因此,介于非IB效应和完全IB效应之间的某种状态似乎更接近现实。此外,非大气源被证明在贡献它们自己的x方面相对重要,特别是海洋角动量,如Ponte等人(1998),Johnson等人(1999)所证明的那样;另见Gross et al.(2003)的综述。
了解极地运动变率的气象起源是有指导意义的。激发项的方差在经常以波动低压为强烈特征的变率区域具有最大的威力,如北太平洋、北大西洋和南大洋地区(Salstein和Rosen, 1989)。虽然大气激发对极运动的影响来自于压力的变化海洋区域在ISV时间尺度上的IB效应在很大程度上减少了,在大陆上空,强半永久高压区域波动,主要在西伯利亚上空,其次在北美上空,影响极运动(Nastula和Salstein, 1999)。
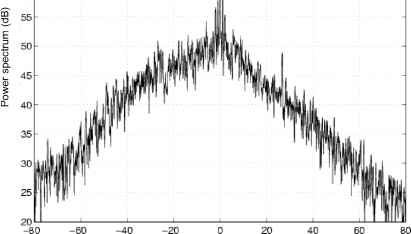
从观测到的极运动激发x的功率谱中,可以获得对ISV的进一步了解,如图8.4所示。既然在这种情况下输入时间序列是复值的,那么正频率和负频率都是有意义的——正频率指的是圆形前进分量(即与主流极运动方向相同),而负频率指的是逆行分量。在这里,我们可以看到一个宽频的红色光谱,它显示了整个宽ISV波段的正(进行)和负(逆行)频率之间非常明显的不对称。因此,AAMxy能量的相当大的分区驻留在逆行带,其周期比相反的前进方向长几天。这种不对称性已被证明源于AAMxy,因为一旦AAMxy从时间序列中减去,这种不对称性就消失了(Gross et al., 1998b)。叠加的是长周期峰值(在中心,频率约为零)、四个季节性峰值(进进+逆行为每年+半年,紧挨着中心峰值,其中最强的是进进年度)和几个孤立的潮汐峰值(例如,由于海洋潮汐,每月和每两周出现一次);所有的时间尺度都与ISV的兴趣尺度相距甚远。
频率(周期/年)
图8.4。从自由钱德勒共振对大地测量观测到的极运动进行反卷积得到的极运动激励功率谱,1976-2003。正频率是指循环前进分量,负频率是指逆行分量。请注意频谱中明显的不对称,在整个宽ISV波段中,负频率的功率要比正频率高得多。
频率(周期/年)
图8.4。从自由钱德勒共振对大地测量观测到的极运动进行反卷积得到的极运动激励功率谱,1976-2003。正频率是指循环前进分量,负频率是指逆行分量。请注意频谱中明显的不对称,在整个宽ISV波段中,负频率的功率要比正频率高得多。
8.2.3角动量和力矩
固体地球和流体包膜之间的角动量传递是由作用在流体-固体地球界面上的力产生的力矩动态完成的。力矩矢量,当然,是力和半径矢量的叉乘。角动量和扭矩之间关系的公式可以在Munk和MacDonald(1960)和Wahr(1982)中找到。基本上,在处理地球自转问题时,人们可以完全依赖角动量守恒,并将AAM的相反变化与固体地球的相反变化等同起来,而不需要事先知道实际传递角动量的实际扭矩。另一方面,人们可以努力建模和计算适当的扭矩,原则上,它应该以与角动量方法中发现的完全相同的方式影响角动量的传递(并保存总角动量)。角动量和扭矩方法是动态等效的,但它们有不同的公式,面临不同的数据可用性和不确定性问题。特别是,扭矩方法目前还不是一门“精确科学”,因为它的研究不足
o - b |
1992 |
山转矩 |
6-1 - 0 -5- |
摩擦力矩i i i i i i i i i i i |
- |
1993 |
|||
- |
1994 |
|||
厘米 |
1 - |
1995 |
||
l |
1996 |
|||
X |
X |
|||
- |
||||
- |
1999 ^ |
1999 |
||
- |
2000 |
1 I 1;11 1 ' 1:1 2000;: "v" ' " ' \ ' ' |
||
- |
2001 |
2001 """ """ """ """ """ """ """ "" v " |
||
图8.5。在与ALOD相关的轴向分量中,有两种不同的大气力矩作用在固体地球上,包括法向山力矩和切向摩擦力矩。请注意山力矩中最高频率的突出,尽管对于ISV时间尺度,山力矩和摩擦力矩具有相当的功率。
图8.5。在与ALOD相关的轴向分量中,有两种不同的大气力矩作用在固体地球上,包括法向山力矩和切向摩擦力矩。请注意山力矩中最高频率的突出,尽管对于ISV时间尺度,山力矩和摩擦力矩具有相当的功率。
了解扭矩机制,因此在其建模中存在较大的不确定性。
以大气和海洋为例,有两种主要类型的力矩,其研究可追溯到怀特(1949)和牛顿(1971)。第一种是摩擦力矩,它来自于陆地和海洋表面的风应力形式的切向力,以及海底阻力;第二种是基于对地形作用的法向力的压力力矩。在大气-陆地和洋陆边界上,压力扭矩分别称为山地扭矩和大陆扭矩。对于大气,它们是由数据同化方案中的模型计算的(例如,Madden和Speth, 1995年)。同样,影响地球自转的海洋扭矩也由Fujita等人(2002)的模型进行了审查和计算。
从根本上说,发生在比大多数一般环流模型的网格尺度更小的范围内的动作,会根据重力波阻力产生额外的扭矩。它已被调整为一个额外的扭矩,尽管它在这里考虑的时间尺度上很小。这种引力波可以看作是水平压力梯度效应的累积;然而,当在模型中描述时,它们类似于摩擦力矩。基于NCEP再分析系统,我们在图8.5中绘制了轴向情况下的两个较大扭矩,即山扭矩和摩擦扭矩。可以注意到,山地扭矩在与风暴和晴朗天气系统穿越山地地形的天气活动有关的高频上具有功率(Iskenderian和Salstein, 1998),导致了上述压力梯度。在这样快速的天气尺度上,摩擦力矩具有低时间变异性,如盛行风在这些时间尺度上,近地表的变化并不明显。时间上的功率谱(未显示)显示,在ISV时间尺度上,摩擦和山力矩的大小相当。Madden(1987)指出,来自对流区东部异常的摩擦力矩可能是40-50天时间尺度上相互作用的原因。
原则上,在流体-固体地球之间的密度异常上存在一个额外的引力力矩(de Viron等人,1999年)。质量,因此重力异常的山脉会对上面的大气质量产生一个额外的力这个力会投射到一个力矩上。火山周围的大气质量变化会产生不均匀的影响,在特定的方向上产生残余力。这种效应在轴向情况下具有非常小的量级,因此没有在图8.5中绘制。然而,对于激发极运动的赤道平面信号,与地球扁圆凸起有关的重力扭矩是重要的,因为地球扁圆率是一个很大的纬度依赖的质量异常。这种重力扭矩在相当大的程度上抵消了将赤道隆起视为地球上一座大山时获得的压力“山”扭矩(Wahr, 1982;贝尔,1994)。然而,这样的引力力矩在ISV时间尺度上有相对较小的变异性,即使在赤道极运动相关的方向上也是如此。然而,在ISV时间尺度上,净凸起扭矩主导了大气对极地运动的影响(Marcus et al., 2004)。
继续阅读:Geocenter运动
这篇文章有用吗?