保形图和保形边界

有一个方便的时空模型的表示方式,特别是在模型具有球面对称的情况下,如Oppenheimer-Snyder和弗里德曼的时空。这是通过使用保形图。我要区分两种类型的保形图,严格和保形图示意图。43[2]我们应当看到的效用。

让我们先从严格的保形图,可用于表示时空(这里用M)与精确的球形对称。©图将是一个地区的飞机,和每一个点的内部©代表整个球体的价值(即SP的价值)的m .得到一幅画的是什么,我们可能会失去一个空间维度,想象旋转该地区©一些垂直线向左(见图2.26)——线被称为一个旋转轴。然后每个点©会描绘出一个圆(S1)。这是对我们的视觉想象力足够好。但对于完整的四维时空M的照片,我们需要一个二维旋转,所以每个内部点©描绘出一个球体(S2) M。

通常,在我们的严格的保形图中,我们发现我们有一个旋转轴边界的一部分地区©。这些边界点在轴代表图作为一个破碎的铁路线将每个代表一个点(而不是一个S2)在四维时空,所以整个折线

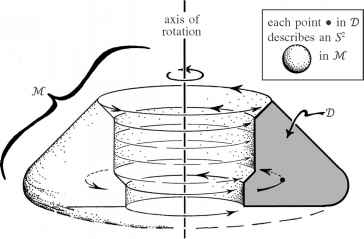
图2.26 Strict V形图用于表示时空(这里用M)与确切的球形对称。二维区域V是旋转(通过一个二维球面S2) 4空间M。

也代表一行在M .图2.27给我们的印象如何,整个时空M是二维空间的构成作为一个家庭与V对北黄海轴旋转。

转动轴转动轴

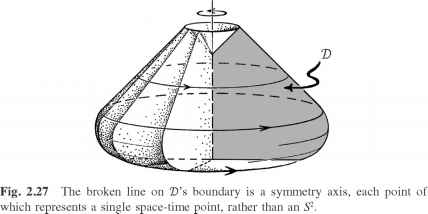
我们要想到M正形时空,而不是过于担心特定扩展,全面度量了M g。

因此,按照最后一句§2.3 M是提供一个完整的家庭(与)零锥。按照这个,D本身,是一个二维子空间的M,继承自二维保形时空结构,有自己的“时间空的锥”。这些仅仅是由一对截然不同的“零”方向每一点的D被认为是面向未来。(他们只是飞机的十字路口定义的副本与未来的零锥M D;见图2.28)。

图2.28 D的“零锥”,在45°垂直的角度,与嵌入式的十字路口M D。

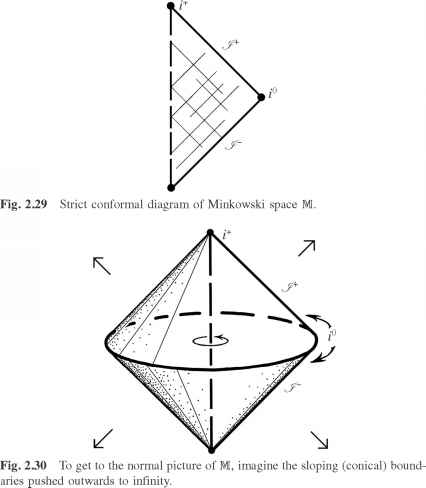
在严格的保形图中,我们尽量安排这些未来零方向D在45°面向垂直向上。说明情况,我画在图2.29中,整个的保形图闵可夫斯基空间- M,径向零线画在45°向上垂直。在图2.30中,我试图说明如何实现这种映射。我们可以看到,图2.29展示了保形图的一个重要特性:图片的仅仅是一个有限的直角三角形,尽管整个无限时空M图包含的。保形图的特征,确实是,他们使无限的时空区域被压扁了的,被环绕的一个有限的画面。∞本身也在图中表示。过去两个大胆的倾斜的边界线代表零无穷J -和未来空无穷J +,在每一个零轴转动轴旋转

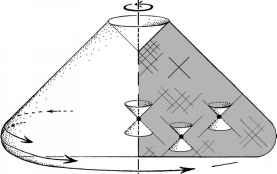
图2.28 D的“零锥”,在45°垂直的角度,与嵌入式的十字路口M D。

测地线(零直线)M获得过去的端点在J - J +未来的终点。(通常是读信雅“scri”——即“脚本我”。)[244]也有三分,我——,钱数,我+边界,分别代表过去的时间无限,spacelike无穷,和未来的时间无限,每一个类时测地线在M获得过去的终点我未来的终点我+,和每个spacelike测地线通过点i0关闭在一个循环。(我们应当看到,不久,为什么i0确实必须被视为仅仅是一个点)。

在这个节骨眼上,它可能有助于回忆艾雪版画图2.3 (c)提供一个正形整个双曲平面的照片。边界圆圈代表其无穷,形有限,在本质上是相似的方式的方式,J2 - i - i0,和我一起+代表无穷M .事实上,就像我们可以扩展双曲平面上,光滑的保形流形,超出其保形边界的欧几里得平面内代表(图2.31),我们也可以扩展M,顺利,其边界以外更大的保形流形。事实上,M形相同的时空模型的部分称为爱因斯坦宇宙£(或者“爱因斯坦缸”)。这个宇宙模型是一个三维空间(S3),完全静态的。图2.32 (a)提供了一个直观的图片这个模型(一个爱因斯坦最初引入宇宙常数为了实现,1917年;看到§2.1)和图2.32 (b)提供了一个严格的保形图代表。注意,在这个图中有两个单独的轴旋转,由两个垂直的虚线表示。这是完全一致的;我们只是认为S2的半径,而内部图中的每个点代表,尽可能缩小到零破碎线是接近。这也可以解释

图2.31扩展双曲平面上,光滑的保形流形,超出其保形边界的欧几里得平面内表示。

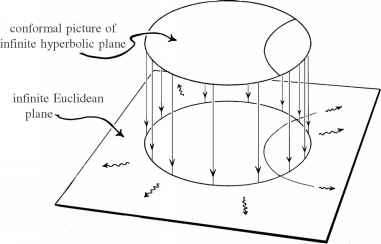
图2.31扩展双曲平面上,光滑的保形流形,超出其保形边界的欧几里得平面内表示。

curious-seeming事实空间无限的M形单点钱数,为S2的半径,它将似乎代表已经缩小为零。空间S3横截面上的时空£源自这个过程。图2.33 (a)展示了M£正形次区域的出现,事实上我们可以考虑整个歧管£组成,形,无限的空间的M \ +的每一个加入到下一个,和图2.33 (b)显示了这是如何实现的严格保形图。这将是值得这张照片的时候我们来考虑第3部分的模型。

	r .我			/ \ / \
t时间	l;J			\ /
(一)		(b)	_	«V

图2.32 (a)直观的爱因斯坦宇宙£(爱因斯坦缸);(b)、(c)严格的保形图的一样的。

图2.32 (a)直观的爱因斯坦宇宙£(爱因斯坦缸);(b)、(c)严格的保形图的一样的。

现在让我们考虑弗里德曼宇宙论在§2.1中引入的。不同情况下K > 0, K = 0 K < 0 = 0,说明在图2.34 (A)、(b)、(c),分别。奇点在这里表示为扭动的线。我引入了一个符号,一个白色边界上的点代表整个球体S2,而黑点“•”(我们已经在M)的情况下代表单点。这些白点代表双曲空间的边界范围,埃舍尔的保形变换在二维情况下使用。相应的情况下积极的宇宙学常数(> 0,

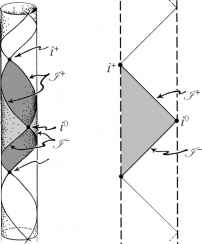
图2.33看出钱数是一个单点。(一)M£conformai次区域的出现。整个歧管£组成,可以被认为是形,无限的空间M;(b)显示了这是如何实现的严格保形图。

图2.34为三种不同的情况下,严格的保形图K > 0, K = 0 K < 0 = 0,弗里德曼的宇宙论。

K > 0我们假设空间曲率并不足以克服和产生终极re-collapse)。这些都是见图2.35 (a), (b)、(c)。这些图可以指出的一个重要特性。未来的无穷J2 * spacelike所有这些模型,最终表明,水平总是比大胆的边界线

图2.34为三种不同的情况下,严格的保形图K > 0, K = 0 K < 0 = 0,弗里德曼的宇宙论。

45°,与未来无限,发生在= 0(在情况见图2.34 (b) (c)和图2.29),在45°的边界在哪里,所以J +然后零超曲面。这是一个普遍的特征之间的关系的几何性质J +和宇宙学常数的值,它将在第3部分对我们至关重要。

图2.35为弗里德曼模型与严格的保形图> 0。(一)K > 0;(b) K = 0;K < 0。

这些弗里德曼模型> 0在他们遥远的未来都有一个行为(即J +)附近的密切接近德西特维时空,宇宙模型是完全空的物质和极其对称(作为一个闵可夫斯基四维球体的模拟)。在图2.36 (a)我已经勾勒出一个二维的版本D,只有一个空间维度代表(全德西特4空间维闵可夫斯基5次太空将是一个超曲面),我给了一个严格的保形图在图2.36 (b)。稳态模型,指在§2.2中,只是一个D的一半,见图2.36 (c)。由于“削减”需要通过D(锯齿形边界)稳态模型实际上是所谓“不完整”,在过去的方向。有普通类时测地线可以代表自由运动的大规模的粒子测量值比早些时候不扩展到一些有限的价值。这可能会被认为是一个令人担忧的缺陷模型中如果应用于未来的发展方向,因为它可以适用于未来的一些粒子或太空旅行者,[245]但是我们可以简单地说,这种粒子运动没有礼物。

继续阅读:结合无穷

这篇文章有用吗?

0 2