熵作为国家统计

但如何物理学家的“熵”的概念,因为它出现在第二定律,实际上量化这一“随机性”,这样确实能看到自我组装的蛋是相当不可能的,从而拒绝作为一个严肃的可能性?为了更明确的关于熵的概念到底是什么,这样我们可以更好的描述实际上第二定律断言,让我们考虑一个简单的例子,而不是打破鸡蛋。第二定律告诉我们,例如,如果我们把一些红漆成一锅,然后蓝漆成同样的锅,给混合搅拌,之后短时间内如此激动人心的不同地区的红色和蓝色会失去自己的个性,和最终的全部内容就会出现紫色制服的颜色。似乎没有进一步的搅拌将紫色的颜色转换回原来的红色和蓝色的区域分离,尽管time-reversibility混合的亚微观的物理过程。事实上,紫色的颜色应该最终自发产生的,即使没有激动人心的,特别是如果我们油漆一点温暖。但随着搅拌,紫色的状态是达到更快。的熵,我们发现初始状态,有明显的分离区域红色和蓝色颜料,将有一个相对较低的熵,但完全紫色颜料的锅,我们最终将会有一个相当大的熵。事实上,整个搅拌过程为我们提供了一个情况,不仅是符合热力学第二定律,但开始给我们的感觉第二定律。

让我们试着成为更精确的关于熵的概念,所以我们可以在这里更明确对正在发生的事情。系统的熵实际上是什么?基本上,这个概念是一个相当基本的一个,虽然涉及一些独特微妙的见解,主要是因为伟大的奥地利物理学家路德维希·玻尔兹曼,和这只计算不同的可能性。让事情变得简单,让我们理想化油漆桶这样只是一个例子(非常大)有限数量的不同可能性的位置每个分子的红漆或蓝色的油漆。我们认为这些分子是红球和蓝球的,这些被允许只占据离散位置,集中N3体积隔间内,我们思考我们的油漆罐作为一个巨大的细分N x Nx N体箱由这些隔间(见图1.2),在那里我假设每个舱都是被一个球,红色或蓝色(分别表示为白人和黑人,图中)。

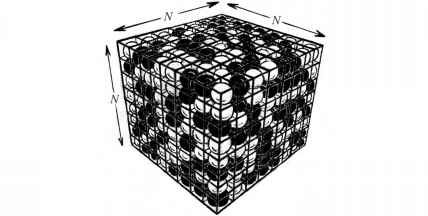
图1.2 Nx Nx N体板条箱,每个隔间包含一个红色或蓝色的球。

油漆的颜色判断在锅里的某个地方,我们做一些平均相对密度的红球蓝球考虑附近的位置。让我们通过包含该位置在一个体积远小于整个箱盒,但非常大的与个人相比体积隔间只是考虑。我假设这个箱子包含大量的隔间就认为,和属于立方阵列的框,填满整箱的方式不如原来的精制隔间(图1.3)。让我们假设每个箱子有一个边长是n倍原来的隔间,这样有n x n n = n3隔间在每个盒子。这里n,虽然仍很大,要远远小于n:

为了保持简洁,我假设N是恰当的倍数,这样

N = kn k是一个整数,让箱子的数量跨度箱每一方。现在会有k x k x k = k3的中型盒整箱。

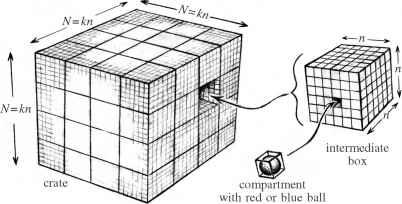
图1.3隔间组成k3的盒子,每个大小n x n n。

这个想法将会使用这些中间框为我们提供的“颜色”,我们看到在那个盒子的位置,在球本身被认为是太小,不足以单独出现。平均会有颜色或色调,可以分配给每个盒子,由“平均”的颜色红色和蓝色球盒子内。因此,如果r是红球在箱子里的数量正在考虑,和b的蓝色球(r + b = n3),色调在这个位置是被定义为r b的比例。因此,我们认为我们得到一个红颜色如果肋骨大于1和一个蓝色色调如果肋骨小于1。

让我们假设混合物看起来对我们是一个统一的紫色,如果每一个n x n n隔间的肋骨有一个值在0.999和1.001之间(r和b是相同的,十分之一的百分之一)的准确性。首先考虑,这似乎是一个相当严格的要求(适用于每一个个人n x n n舱)。但当n变得非常大,我们发现绝大多数球安排做满足这个条件!我们还应该记住,当考虑分子一罐油漆,他们的数量多得惊人,普通标准。例如,很可能是类似于一个普通的1024个分子可以油漆,所以采取N = 108不会是不合理的。同时,因为会很明显,当我们考虑颜色看起来完美的数字显示照片像素大小只有10厘米,带一个值k = 103也很合理,在这个模型中。从这里,我们发现,这些数字(N = 108 k = 103,所以N = 105)大约有1023570000000000000000000000不同的安排整个收集V2N3红色球和V2N3蓝色球给统一的紫色的外观。只有区区1046 500000 000000给的原始配置的不同安排的蓝色是完全在顶部和底部的红色完全。分布式完全随机的,因此,对于球的概率找到统一的紫色是一个虚拟的肯定,而找到所有的概率顶部的蓝色的有点像10 - 23570000000000000000000000(这个数字并不是大大改变如果我们不需要所有的顶部的蓝色球是最初,但说,只有99.9%的人在顶部)。

我们认为的“熵”之类的这些概率,或者相反,这些不同数量的安排,给相同的整体外观。实际上,直接使用这些数字会给一个非常任性的测量,由于他们的巨大差异的大小。因此它是幸运的,有良好的理论原因以这些数字的对数(自然)为一个更合适的“熵”措施。对于那些读者不太熟悉对数的概念(特别是的自然对数),让我们短语事情的以10为底的对数送往——把这里称为“log10”(而不是自然对数,使用后,我将简单地称为“日志”)。要理解log10,基本要记住是logio 1 = 0, logio 10 = 1, logio 100 = 2, logio 1000 = 3, logio 10000 = 4,等等。

即获得log10 10的力量,我们只是数0的数量。(正整数),不是一个10的力量,我们可以概括地说,组成部分(即小数点前的数量)的log10获得通过计算数字的总数,再减去1,例如(黑体组成部分类型)

logio 2 = 0.301029995 66。logio 53 = 1.724275 86960。logio 9140 = 3.960946195 73。

等,所以在每种情况下以粗体显示的数量只是一个不到数字log10被的数量。最重要的财产log10(或日志)是它将乘法运算转换为加法;那就是:

logio (ab) = logio + logio b。

(在10 a和b都是大国,这是明显的从上面,因为= 10 ^乘以b = 10 b给我们ab = 10 ^)。

上面显示的意义与使用对数熵的概念是我们希望系统的熵由两个独立的和完全独立的组件被简单地添加我们得到的各个部分的熵。我们说,从这个意义上说,熵概念是添加剂。事实上,如果第一个组件可以在P不同方式和第二部分在不同的方式,然后会有不同方式的产品PQ整个系统的组件组合在一起可以出现(因为每个P安排给第一个组件将会有完全问安排给第二个)。因此,通过定义的熵状态的任何系统的对数成正比的不同方式,国家可以,我们确保这个添加属性,对于独立系统,确实会感到满意。

然而,我已经有点模糊,到目前为止,关于我的意思的多种方式,系统的状态可以发生的。首先,当我们模型分子的位置(在一罐油漆,说),我们通常不考虑现实的离散的隔间,因为在牛顿理论,详细,有无限数量的不同可能的位置每个分子而不是有限。此外,每个分子可能是一些不对称的形状,所以它可以面向空间以不同的方式。也可能有其他类型的内部自由度,如扭曲的形状,必须相应的考虑。每一个这样的取向或变形必须被视为一个系统的不同的配置。我们可以处理所有这些点通过考虑所谓的配置空间系统,我下一个描述。

维自由度,系统的配置空间将是一个采用空间。例如,如果系统由particlespi问点,p2,…,pq(每个没有任何内部自由度),然后配置空间3 q维度。这是因为每个粒子只需要三坐标来确定它的位置,所以有3 q整体坐标,即单点P的配置空间定义的位置π,p2,…一起,pq(见图1.4)。在更复杂的情况下,哪里有内部自由度如上所述,我们将有更多的自由度对于每一次这样的粒子,但总的想法是相同的。当然,我并不期望读者能够“可视化”在如此高的空间维度。这不会是必要的。我们将得到一个好主意如果我们想象事情在二维的空间(如区域画在一张纸上)或普通三维空间的一些地区,如果我们总是记住这样的可视化将不可避免地在某些方面是有限的,其中的一些我们将很快来到。当然,我们应该永远记住,这样的空间是纯粹的抽象数学的不应被混淆的三维物理空间或四维物理时空的普通的经历。

图1.4配置空间C问点particlespi, p2,…,pq 3 q-dimensional空间。

有进一步需要澄清一点,我们的尝试熵的定义,这是什么问题我们正在努力。在我们有限的模型的情况下,我们有有限数量的不同安排红色和蓝色球。但是现在我们有无限的安排(因为粒子位置需要连续参数),这使我们考虑高维卷在配置空间,为我们提供一个适当的大小,而不是计算离散的事情。

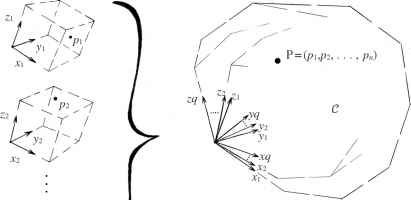
配置空间C问点粒子π,p2,。,pq 3 q-dimensional空间

了解什么是“量”的一个高维空间,这是一个好主意认为较低的维度。容积量度的二维曲面的一个地区,例如,是衡量区域的面积。在一维空间的情况下,我们想简单的长度沿曲线的一部分。在一个n维配置空间,我们会考虑一些n维模拟卷的一个普通3-volume地区。

但我们的区域配置空间测量的量,当我们关心的熵的定义吗?基本上,我们是关心的是整个地区的数量配置空间对应的集合状态的看起来一样的特定状态下考虑。当然,“看起来一样”是一个相当模糊的短语。真正的意思是,我们有一些合理详尽的宏观参数测量诸如密度分布,颜色,化学成分,但我们不会关心每个原子的精确地点等详细事项构成系统考虑。这个配置空间的分割C到区域看起来一样的在这个意义上被称为“粗粒化”C。因此,每一个点代表国家的粗粒度的地区包括,被认为是互相区别,通过宏观测量。见图1.5。

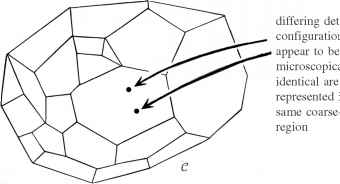
图1.5的粗粒度的C。

显微镜下相同的相同的粗粒度的地区代表不同的详细的配置

图1.5的粗粒度的C。

当然,何谓“宏观”测量,仍是相当模糊的,但我们正在寻找一些模拟的“色调”概念,我们关心在我们上方可以简化有限元模型的油漆。诚然有一些模糊性在这样一个粗粒度的概念,但它的体积是这样的地区配置空间或相反,体积的对数的粗粒度的地区,我们关心的是熵的定义。是的,这仍是一个有些模糊,但值得一提的是,健壮的熵的概念是,尽管如此,主要是由于绝对惊人的比率的粗粒度的卷,卷。

继续阅读:相空间和玻尔兹曼熵的定义

这篇文章有用吗?

+ 2 0