相空间和玻尔兹曼熵的定义

我们还没有完成熵的定义,然而,一直说到目前为止只解决了一半的问题。中我们可以看到一个不足描述到目前为止通过考虑一个稍微不同的例子。而不是让一罐红色和蓝色的油漆,我们可能会考虑一个瓶子装满水的一半,一半用橄榄油。我们可以尽可能多的搅拌,同时摇动瓶子。但几分钟后,橄榄油和水分开,我们很快就有橄榄油的上半部分底部的瓶子和水的一半。熵的增加中分离过程,不过。这里的新观点是有很强的分子间相互吸引的橄榄油使他们聚集,从而排出水。仅配置空间的概念并不足以解释熵增加在这种情况下,当我们真的需要考虑单个粒子的运动/分子,而不仅仅是他们的位置。他们的动作会是必要的对我们来说,在任何情况下,这样的未来演化状态是决定,根据牛顿定律,我们假设手术。在分子的橄榄油,引起他们强烈的互相吸引他们的速度增加(在充满活力的轨道运动彼此)当他们靠近在一起,它是“运动”相关的一部分空间提供所需的额外的体积(因此额外的熵)的情况下,橄榄油被收集在一起。

我们需要的空间,在上述配置空间C,是所谓的相空间。相空间T有两倍维度(!),C,和每个位置坐标构成粒子(或分子)必须有一个相应的“运动”坐标除了那个位置坐标(见图1.6)。我们想象这样适当的协调将是一个测量的速度(或角速度,角坐标描述方向的空间)。然而,事实证明(因为深连接形式的哈密顿理论[11]),这是动量(或角动量,在角坐标的情况下),我们将需要为了描述运动。在最熟悉的情况下,我们需要知道这个“动量”概念是质量乘以速度(§1.1中已经提到)。现在(瞬时)运动,以及位置,所有的粒子构成我们的系统编码在T .单点p的位置我们说我们的系统的状态描述p T内的位置。

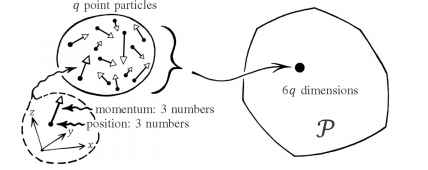
图1.6 T相空间维度为C的两倍。

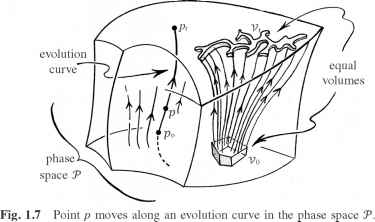
动态的法律,我们正在考虑,管理我们的系统的行为,我们不妨把它们牛顿运动定律,但我们还可以治疗更一般的情况下(如连续场的麦克斯韦电动力学;看到§2.6,§3.1,§3.2,和附录A1),也受到广大哈密顿框架(上图)。这些法律是决定性的,我们的系统在任何时候的状态完全决定了国家在其他任何时候,是否早或晚。将事情的另一种方式,我们可以描述系统的动态演化,根据这些法律作为p点沿着一条叫演化曲线相空间t演化曲线代表了整个系统的独特的进化动力学规律,从初始状态开始,我们可以通过一些特定点p0代表相空间t(见图1.7)。事实上,整个相空间T将填满(技术层状)这样的进化曲线(就像一捆稻草),在每一个点(T)将躺在一些特定的演化曲线。我们必须认为这条曲线是oriented-which意味着我们必须分配一个方向的曲线,我们可以通过将一个箭头。我们的系统的演变,根据动态法,是被一个移动的点p,旅行沿着进化曲线这种情况下从特定点p0,箭头的方向移动的点。这为我们提供了未来的进化系统的特定状态演化曲线后由p。远离p0方向相反的方向的箭头给time-reverse进化,这告诉我们出现p0所代表的国家如何从州在过去。这进化将是独一无二的,根据动态法。

相空间的一个重要特征是,由于量子力学的出现,我们发现它有一个自然的措施,这样我们可以卷在相空间,从本质上说,是无量纲数。这很重要,因为波尔兹曼熵的定义,我们必不久,相空间的卷,所以我们需要相互比较高维体积措施,尺寸可能差别很大从一个到另一个。这可能看起来很奇怪从普通古典的观点(即non-quantum)物理,因为在普通条款我们会认为曲线的长度(一维“卷”),总有一个较小的测量比表面的面积(二维“卷”),和一个面积是较小的测量比3-volume,等等。但相空间的措施卷量子理论告诉我们使用的确只是数字,在衡量单位的质量和距离给我们h = 1,普朗克常数的数量被狄拉克的版本(有时称为“减少”普朗克常数),h是原始的普朗克常数。在标准的单位,h极小值h = 1.05457。x 10-34焦耳秒,所以我们遇到的相空间的措施一般情况下往往有非常大的数值。

想到这些数字是整数(整数)给某些“粒度”相空间,这提供了量子力学的“量子”的不连续性。但在大多数普通情况下这些数字将是巨大的,所以粒度和离散性是没有注意到。异常出现的普朗克黑体谱我们将来到§2.2(见图2.6和1.2注),这是观察到的现象,马克斯·普朗克的理论分析解释说,1900年,从而推出量子革命。这里必须考虑一个平衡情况同时涉及不同数量的光子,因此相位空间不同的维度。适当的讨论这些问题超出了本书的范围,[13]但我们将回到§3.4中的量子理论的基础知识。

图1.8粗粒度的更高维度的印象。

现在我们有了一个系统的相空间的概念,我们将需要了解第二定律运作之间的关系。上面的与我们讨论的配置空间,这就要求我们提供一个粗粒度的T的两个点属于同一个粗粒度的地区将被视为“区别”对宏观参数(如温度、压力、密度、流体流动的方向和大小,颜色,化学成分,等等)。熵的定义的状态由一个点p T是现在提供的非凡的玻耳兹曼公式V是粗粒度的区域的体积含p。量k是一个小的常数(本来玻耳兹曼常数有我选择使用一个自然对数,“日志”;它是由k = klog10(日志10 = 2.302585。),k确实是玻尔兹曼常数,和k的微小值k = 3.179。x 10-23 JK-1(见图1.8)。事实上,是一致的

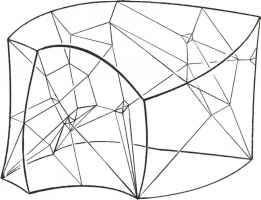
图1.8粗粒度的更高维度的印象。

5 = k V逻辑,k = 1.3805。x 10-23焦耳/ k,通常所用的定义的物理学家,今后我将回归自然对数和玻尔兹曼熵公式写成

在我们继续之前,在§1.4中,探索的合理性和意义这优雅的定义,以及它如何与第二定律,我们应该感谢一个特定的问题是很好解决的。有时人们(完全正确)指出,卑贱的熵状态不是很好衡量的“特殊性”。如果我们再次考虑蛋下降的情况,介绍了在§1.1中,我们注意到相对熵值状态时抵达蛋变得一团糟在地板上仍然是一个非常特殊的一个。特殊是因为有一些非常特殊的粒子的运动构成之间的相关性,明显的“混乱”——这样的自然,如果我们逆转,那么混乱将会显著属性,它将迅速解决使自己陷入了一个完美的完成了鸡蛋,项目本身向上,鲈鱼本身上面小心翼翼地放在桌子上。事实上,这是一个非常特殊的状态,没有特殊低于相对低熵的配置鸡蛋在桌子上。但是,“特殊”组成的国家混乱无疑在地板上,特别在特定的方式,我们称之为“低熵”。卑贱的熵是指体现专业,这是在特殊的宏观参数值。细微的粒子运动之间的相关性是不相干的,当涉及到的熵是分配给系统的状态。

我们看到,尽管一些州的相对较高的熵(如时间反演砸蛋只是考虑)可以发展低熵状态,与第二定律相矛盾,这些将是一个非常少数的可能性。可以说,这是“重点”的概念熵和热力学第二定律。玻耳兹曼熵的定义的概念的粗粒化处理此事的“特殊”要求的低熵很自然的和适当的。

另外一个观点是值得。有一个关键的数学定理称为刘维定理,断言,对于正常类型的古典动力系统被物理学家(标准哈密顿系统称为上图),相空间中的氧化保护卷。这是右边所示图1.7的一部分,我们看到,如果一个地区的签证官,体积V, T在相空间,是由进化曲线区域Vt,时间T后,然后我们发现Vt一样具有相同的体积V签证官。然而这并不违背热力学第二定律,因为粗粒度的地区不保存的进化。如果初始区域签证官恰巧是一个粗粒度的区域,然后Vt将可能是一个体积庞大的混乱传播从一个更大的粗粒度的地区,或者几个这样的地区,在稍后的时间t。

结束本节,将适当的回归的重要物质使用对数在玻耳兹曼公式,跟进§1.2中被暂时解决的一个问题。这件事会对我们特别重要之后,尤其是在§3.4。假设我们正在考虑物理在我们当地的实验室,我们希望考虑熵的定义一些结构参与实验,我们执行。我们认为是玻尔兹曼熵的定义与我们的实验吗?我们将考虑所有自由度的问题,在实验室里,并使用这些定义一些相空间内T T将相关的粗粒度的区域体积V V,给我们的玻耳兹曼熵klogV。

然而,我们可能会选择考虑我们的实验室作为一个更大系统的一部分,让我们说剩下的整个银河系内我们居住,那里有非常多的自由度。通过包括所有这些自由度,我们发现我们的相空间比以前将会非常大。此外,粗粒度的地区相关熵的计算在我们实验室现在也会非常大,因为它可以涉及所有在场的自由度在整个星系,不仅这些实验室的相关内容。然而,这是自然的,因为现在的熵值,适用于整个星系,熵参与我们的实验只是一小部分。

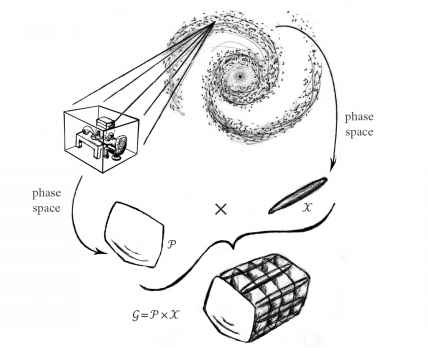
图1.9相空间被实验者认为只是一个小因素,其中包括所有的外部自由度的星系。

参数定义外部自由度(确定星系的状态,除了那些定义状态在实验室)为我们提供了一个巨大的“外部”相空间X,和将会有一个粗粒度的地区内W X特征状态的星系外部的实验室。见图1.9。相空间Q为整个星系将定义的完整的一套参数,外部(X)提供的空间和内部空间(P)提供了空间。问,数学家,P的产品spaceilA] X,写

Q = P x x,及其维度将之和维度(T)和x(因为它的坐标是(T)紧随其后的x)。图1.10展示了产品的概念空间,其中T是一个平面和x线。

图1.10的产品空间,T是一个平面和X是一条直线。

如果我们把外部自由度完全独立的内部的,然后问相关的粗粒度的地区将是产品的粗粒度的地区V ?分别在X和W(见Fig.1.11)。此外,体积元素在产品空间被产品的体积元素在每个成分的空间;因此粗粒度的区域的体积V x W Q的大众产品体积V粗粒度的地区?与体积粗粒度的地区的W W x因此,对数的“product-to-sum”属性,我们获得的玻耳兹曼熵之和的实验室中的熵和熵外部的实验室。这就告诉我们,独立的系统的熵只加在一起,表明一个熵值是可以分配给任何一个物理系统的一部分,是独立于系统的其余部分。

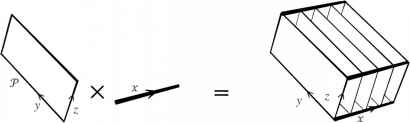
图1.10的产品空间,T是一个平面和X是一条直线。

Vx W

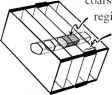
粗粒度的

粗粒度的地区V P

地区V x W问粗粒度的Orf地区W x

图1.11粗粒度的产品区域作为一个产品的粗粒度的地区因素。

T的情况考虑在这里指的是自由度相关实验室和X相关的外部星系(假定相互独立的),我们发现熵值klogV实验者将分配实验执行,如果被忽视外部自由度,将不同于klog熵值(大众)的结果,如果这些外部自由度也考虑在内,通过熵值klogW将分配给所有外部星系的自由度。这个外部部分为实验者没有作用,因此可以安全地忽略研究实验室内部第二定律的作用。然而,当在§3.4我们来考虑的熵平衡宇宙作为一个整体,而最particul是,由于黑洞的贡献,我们将发现这些问题不容忽视,并将获得的基本意义我们!

继续阅读:我们的宇宙膨胀

这篇文章有用吗?

+ 4 2