时空空保形几何锥指标

,1908年,著名的数学家之一赫尔曼闵可夫斯基——巧合被爱因斯坦在苏黎世Polytechnic-demonstrated老师,他可以封装狭义相对论的基础知识一种不同寻常的四维几何而言,爱因斯坦不甚热衷这个想法。但是后来他意识到闵可夫斯基时空的几何概念的重要性。事实上,它形成了自己的一个基本要素概括闵可夫斯基的建议提供他的广义相对论的时空弯曲的基础。

闵可夫斯基4空间整合的标准三维空间的第四个维度来描述时间的流逝。因此,这个4空间的点经常被称为事件,因为任何这样的点时间以及空间规范。真的没有什么非常革命,只是本身。但关键闵可夫斯基的主意是从革命性,他4空间的几何不自然分离成一个时间维度和(更重要的)家庭的普通的欧几里得3个空间,一个为每个给定的时间。相反,闵可夫斯基时空的一种不同的几何结构,给欧几里得奇妙古老的几何的概念。它提供了一个整体几何时空,成为一个不可分割的整体,这完全编码结构的爱因斯坦的狭义相对论。

因此,在闵可夫斯基的4-geometry,现在我们不认为时空是简单地建立起来的一系列3-surfaces,分别代表我们所认为的“空间”在不同的时间(图2.10)。解释,这些3-surfaces描述一个家庭的事件都将被同步。在狭义相对论中,“同时”的概念空间上分开的事件并没有绝对的意义。相反,“同时性”将取决于一些任意选择的观察者的速度。

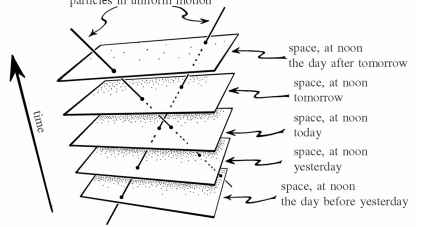
图2.10在闵可夫斯基时空。

当然,这是与普通的经验,因为我们做的似乎遥远的事件的同时性的概念是独立于我们的速度。但(根据爱因斯坦的狭义相对论)如果我们移动速度可比与光,然后事件,似乎我们同时似乎通常不会同时其他一些这样的观察者,用不同的速度。此外,速度甚至不需要非常大,如果我们关心的是遥远的事件。举个例子,如果两人漫步过去彼此相反的方向沿着一条路径,然后在仙女座星系的事件,他们将每个单独考虑与特定事件的同时,他们需要通过可能会相差几周,[225]见图2.11。

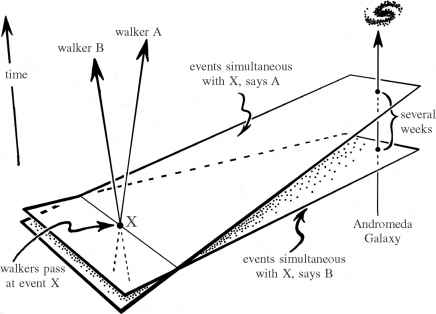
图2.11两个行人漫步过去,但他们的传递事件X是根据每个与事件同步在仙女座不同的几个星期。

根据相对论,“同时”的概念,对于遥远的事件,并不是一个绝对的事情,但取决于一些观察者指定的速度,所以时空的分割成一个家庭的同时3个空间是主观的,不同的观察者速度我们得到不同的切片。闵可夫斯基时空的实现提供一个客观的几何学,这不是依赖任意观察者的世界观,并没有改变一个观察者被另一个取代。在某种意义上,闵可夫斯基所做的是把“相对论”的狭义相对论理论,并给我们一个绝对时空活动的照片。

但对于这个公司给我们图片,我们需要一种结构4空间代替时间连续的3个空间的想法。这是什么结构?我将使用字母M表示闵可夫斯基的

4空间。闵可夫斯基最基本的几何结构分配给M是一个空锥的概念,26[2],描述了光在任何特定事件传播p M .零光锥双锥与常见的顶点在p-tells我们“光速”是在任何方向,在p(见图2.12 (a))。零锥的直观的图片是由一束光,一开始向内聚焦本身正是对事件p零锥(过去),之后,立即传播本身从p(未来空锥),在p像爆炸的闪光,所以空间描述(图2.12 (b))爆炸后成为扩大一系列同心球体。在我的图,我将倾向于画零锥与表面垂直倾斜约为45°,这是我们得到的如果我们选择空间和时间单位,光速c = 1。因此如果我们选择秒时间尺度,然后选择一个light-second(= 299 792 458米)为我们单位的距离;如果我们选择年时间尺度,那么我们选择一光年(= 9.46 x 1012公里)为我们单位的距离,等。[2.27]

图2.12 (a)零锥p在闵可夫斯基4空间;(b) 3维描述未来的锥作为扩大一系列同心球体原始p。

爱因斯坦的理论告诉我们,任何大规模的粒子的速度必须小于的光。在时空方面,这意味着这种particle-this的世界线的轨迹的事件构成了粒子在零的历史学应当被引导

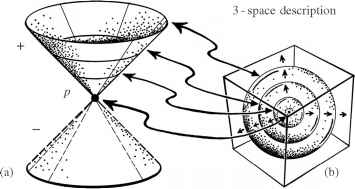
图2.12 (a)零锥p在闵可夫斯基4空间;(b) 3维描述未来的锥作为扩大一系列同心球体原始p。

锥的每个事件。见图2.13。粒子可能会加速的运动在一些地方在世界线,从它的世界线不需要直,加速度被表达,在时空方面,作为一个世界线的曲率。世界线是弯曲的,这是世界线的切向量必须位于零锥。如果是无质量的粒子,光子等[228],那么它的世界线必须躺在空锥在每个事件,因为其速度每一个事件确实是光速。

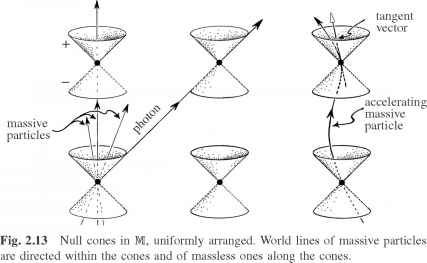
零锥也告诉我们关于因果关系,这是决定哪些事件的问题被认为是能够影响其他事件。的一个原则(特殊)相对论断言信号不得传播速度超过光速。因此,在M的几何学方面,我们说一个事件p将允许对事件因果影响问如果有一个世界线连接p, q,这是一个从p, q(平滑)路径躺在或在零锥。为此,我们需要指定一个方向的道路(附加一个“箭头”路径),统一,从过去到未来。这要求M几何被分配的时间取向,这相当于一个一致的连续单独分配表示“状态”的“过去”和“未来”的两个组件零锥。我已经将过去的组件用“-”符号和一个未来的组件与一个“+”的迹象。这是无花果所示。2.12 (a)和2.13,我过去零锥是杰出的图纸在哪里使用破碎线。正常的“因果关系”术语需要因果影响继续过去到未来的方向,即在面向世界线的切线向量点或在未来零锥。29 [2]

M的几何形状是完全统一的,每个事件都是平等与其他事件。但当我们传递给爱因斯坦的广义相对论,这种一致性通常丢失。尽管如此,我们又有一个连续赋值与时间有关的零锥,又确实,任何大规模的粒子的世界线(面向未来)切矢量位于这些未来零锥。之前,一个无质量的粒子(光子)世界线的切线向量的所有谎言零锥。在图2.14我已经描述的情况发生在广义相对论中,零锥在哪里不是现在安排在一个统一的方式。

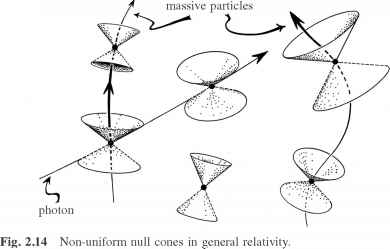
我们必须尽量把这些锥被画在某种理想的橡胶板与零锥印刷。我们可以移动橡胶板和扭曲在任何我们喜欢的方式,只要变形是顺利完成的,在零锥携带橡胶板。零锥确定事件之间的因果关系结构,这是不被任何这样的变形提供了改变锥被认为是携带的表。

有点类似的情况是由埃舍尔的描述双曲平面无花果所示。2.3 (c),在§2.1,我们可以想象埃舍尔的照片印在这样一个理想的橡胶板。我们可以选择的恶魔之一似乎是靠近边界,并移动它,通过这样一个平滑的变形表,所以它进入附近的位置以前是由一个中心。这个运动可以携带所有的恶魔进入位置之前被其他恶魔,和这样的运动描述潜在的对称双曲几何埃舍尔的照片所示。在广义相对论中,对称这种可能发生(与弗里德曼模型中描述§2.1),但这是相当特殊。然而,实施的可能性,这种胶板的变形是非常一般理论的一部分,这些被称为“解析”(或“通用坐标转换的)。我们的想法是,这种变形不改变身体状况。“一般协方差”的原则,这是爱因斯坦的广义相对论的基石,是我们制定物理定律等这样的胶板变形(解析)不改变空间的物理意义的属性和其内容。

这并不是说,所有的几何结构是丢失,唯一仍为我们空间的几何性质的可能只是它的拓扑(事实上有时被称为“胶板几何”,在这表面的茶杯是相同的戒指,等等)。但我们必须小心指定结构是必要的。廖一词经常用于这样一个空间,一些明确的有限数量的维度(我们可以引用一个歧管n维度作为n-manifold),一个歧管光滑但不一定分配任何进一步的平滑度和拓扑结构。在双曲几何的情况下,实际上是一个概念的指标分配给manifold-a数学张量的数量

(参见§2.6),通常用字母g这可能被认为是提供一个转让长度30[2]任何有限的空间中光滑曲线。任何变形的橡胶板的构成这廖会随身携带任何曲线C连接一对点p, q (p和q也由变形)和C的段的长度加入p, q交办g是被认为是不受这个影响变形(在这个意义上,g也是“携带”的变形)。

这个长度概念也意味着一个直线的概念,称为测地线,这样一个直线l被任意两点的事实特征对l p和q,相隔不远,最短的曲线(g)所提供的长度从p q是事实上的部分pq l。见图2.15。(从这个意义上说,测地线提供了“两点之间最短路线”)。我们也可以定义两条光滑曲线之间的角度(这也决定一旦给出g),这样我们可以使用普通的几何观念一旦g。然而,这种几何通常不同于熟悉的欧几里德几何学。

图2.15度规g指定长度曲线以及它们之间的角度。测地线l提供了“p和q之间的最短路线”在这个矩阵g。

埃舍尔的双曲几何的照片(图2.3 (c), Beltrami-Poincare保形变换)因此也有其直线(测地线)。这些可以理解的背景curvi长度测量曲线由g g夹角矩阵行列式值的长度curvi衡量g曲线矩阵行列式值之间的角度

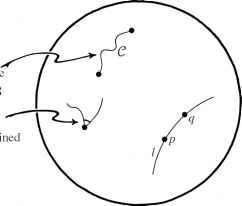
图2.15度规g指定长度曲线以及它们之间的角度。测地线l提供了“p和q之间的最短路线”在这个矩阵g。

欧几里德几何学中这个数字表示,如圆弧边界圆在直角(见图2.16)。把a和b是弧的端点通过两个给定的点p和q,双曲g-distance p和q是之间

C日志

我qbWpal这里使用的“日志”是一种自然对数(2.302585。倍的logio§1.2),“| qa |”等在后台被普通的欧几里得距离空间,和C是一个积极的常数称为pseudo-radius双曲空间。

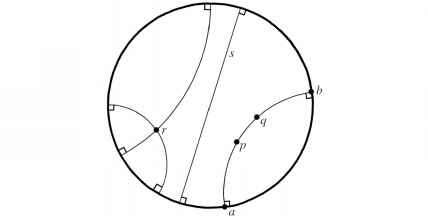
图2.16“直线”(大地测量学)的保形变换双曲几何圆形阿瑞斯会议在直角边界圆。

但而不是指定结构提供了这样一个g,你可以分配一些其他类型的几何。那种将成为我们最关心的是几何称为保形几何。这个结构提供了一个衡量两条光滑曲线之间的角度,在任何时候,他们相遇,但“距离”或“长度”的概念没有指定。正如上面提到的,角的概念实际上是由g,但g本身不是固定的角的概念。虽然保形结构不固定长度测量,它修复长度的比率措施在不同的方向在任何时候

所以它决定了无穷小的形状。我们可以重新调节上下这个长度测量在不同的点不影响保形结构(见图2.17)。我们表达这个重新调节g ^ n2 g n是一个正实数定义的每一点,随空间变化平稳。因此g和n2g给我们相同的保形结构无论积极n我们选择,但g和n2g给我们不同的度量结构(如果n ^ 1),其中n是规模变化的因素。(n的原因出现在“平方”的表达方式“n2g”是表达式的直接措施空间或时间分离,由g,源自的平方根(见注2.30)。)回到埃舍尔的图2.3 (c),我们发现双曲平面的共形结构(尽管不是其度量结构)实际上是相同的欧几里得空间内部边界圆(还不同于整个欧几里得平面)的保形结构。

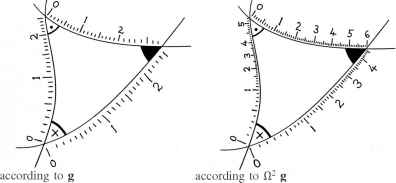
长度不同,但角度同意

图2.17共形结构不固定长度测量,但它确实解决角度通过长度之比在任何时候措施在不同的方向。长度测量可以在不同的点新向上或向下而不影响保形结构。

长度不同,但角度同意

图2.17共形结构不固定长度测量,但它确实解决角度通过长度之比在任何时候措施在不同的方向。长度测量可以在不同的点新向上或向下而不影响保形结构。

当我们来到时空几何,这些想法仍然适用,但也有明显的差异,由于“扭曲”,闵可夫斯基引入欧几里德几何的思想。这个转折是数学家所说的度规的签名。在代数方面,这仅仅是指几+符号改为-符号,它基本上告诉我们多少人一组n相互正交的方向,为一个n维空间,被认为是“时间”(零锥内)和多少“spacelike”(零外锥)。在欧几里德几何,其弯曲的版本被称为黎曼几何,我们认为所有的方向是spacelike。通常的“时空”的想法只涉及1类时的方向,在这样的一组正交,其余spacelike。我们称之为闵可夫斯基如果它是平的,洛伦兹曲线。(洛伦兹)普通类型的时空,我们正在考虑在这里,n = 4,签名是“1 + 3”4个相互正交的方向分离成1类时方向和3 spacelike的。spacelike方向之间的正交性(和之间的类时,我们有超过1)即是成直角,而spacelike和类时方向几何上看起来更像是形势描绘在图2.18中,正交方向的对称与它们之间的零方向有关。身体上,观察者方向类时认为事件是谁的世界线正交spacelike方向同步。

图2.18“正交性”的spacelike和类时方向在洛伦兹时空,在欧几里得图的零锥是直角。

在普通的欧几里得或黎曼几何,我们倾向于认为长度的空间分离,这是我们的东西

洛伦兹

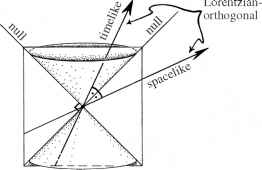
图2.18“正交性”的spacelike和类时方向在洛伦兹时空,在欧几里得图的零锥是直角。

洛伦兹或许用一把尺子来衡量。但什么是统治者,在(闵可夫斯基或洛伦兹)时空条件如何?立即地带,这不是最明显的小工具测量空间分离两个事件之间p和q,见图2.19。我们可以把p在一个边缘地带和q。我们也可以认为统治者狭窄和未加速的,这样的时空曲率影响爱因斯坦的广义相对论(洛伦兹)不相关的,并根据狭义相对论的治疗应该足够了。但根据狭义相对论理论,为了使距离测量提供的统治者给正确的p和q之间的时空分离,我们要求这些事件是同步静止座标的统治者。我们如何确保这些事件实际上是同时在统治者的静止座标?我们可以使用爱因斯坦的原始类型的论点,虽然他更多想到的是火车的统一运动,比ruler-so现在让我们短语太的事情。

统治者的历史

(或训练)

闵可夫斯基空间M

统治者的历史

(或训练)

闵可夫斯基空间M

不同时静止座标光谱中所以分离qp不是统治者的统治者的统治者统治者时间长度不同时静止座标光谱中所以分离qp不是统治者的统治者的长度

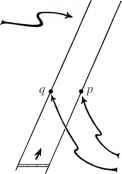
图2.19 spacelike分离点p和q M是不能直接测量的统治者是一个二维地带。

让我们参考的火车(统治者)包含事件p面前,和最终包含问。我们想象一个观察者位于前面,发出光信号从一个事件r的火车,时间,准时到达那里正是事件问,于是立即信号反射回前面,被观察者接收到的事件s。见图2.20。然后观察者法官q和p,同时在火车的静止座标,如果p发生之间的一半排放和最终接收的信号,即如果时间间隔从r p恰恰是一样的,从p s。火车的长度(即统治者)然后(才)同意p和q之间的空间间隔。

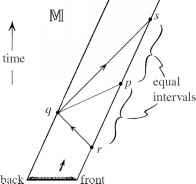
图2.20统治者(或训练)措施分离pq只有当它们同时,所以需要光信号和时钟。

我们注意到,这不仅是更复杂的比简单地放下尺子的测量空间分离的事件,但实际上是由观察者将测量时间间隔rp和ps。这些(平等)直接提供的测量时间间隔的空间间隔pq确定(在单位光速c被统一)。这说明了关于时空度规的关键事实,即它是真的有更直接的测量时间,而不是距离。而不是提供曲线的长度测量,它直接为我们提供了一个测量的时间。此外,并不是所有的曲线都分配一个时间测量:它是曲线称为因果,粒子的世界线,这些曲线被各地类时(与零锥内切线向量,通过大规模粒子)或null(与沿空锥切向量,通过无质量粒子)。什么时空度规g是指定一个时间测量的有限段因果关系曲线(时间衡量的贡献为零的任何部分曲线是null)。从这个意义上讲,“几何”的指标时空拥有真正应该叫做“测时法”,是爱尔兰著名的相对论理论家约翰·l·辛格表示。12311年是很重要的广义相对论理论的物理基础极其精确的时钟确实在自然界中存在,在基本层面上,因为整个理论取决于自然定义度量g。[232]事实上,这次测量是相当物理学的中心,有一个清楚的任何个人(稳定)大规模粒子发挥作用作为一个几乎完美的时钟。如果m是粒子的质量(假定为常数),然后我们发现它有一个剩余能量(2331 E由爱因斯坦著名的公式

E = mc2,这是相对论的基础。另一方面,几乎同样著名的formula-fundamental马克斯-普朗克的量子理论

E =高压

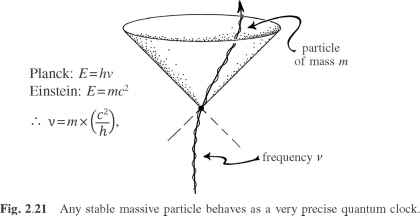
普朗克常数(h),告诉我们,这个粒子的静止能量为它定义一个特定的频率v的量子振荡(见图2.21)。换句话说,任何稳定的大规模粒子的行为作为一个非常精确的量子时钟“滴答走”的特定频率

V = m©,它的质量成正比,通过常数(基本)数量c2 / h。

事实上一个粒子的量子频率非常高,而且不能直接利用可用的时钟。时钟,可以用在实践中,我们需要一个系统包含许多粒子,组合在一起并适当地表演。但关键是,构建一个时钟我们需要质量。无质量粒子(如光子)不能用于构成一个时钟,因为他们的频率必须是零;光子会直到永恒之前其内部“时钟”变得更首次“滴答”!这一事实将在稍后对我们具有重要意义。

这一切都是按照图2.22中,我们看到不同的相同的时钟,所有在同一eventp原始,但以不同的速度运动,可以比得上但低于光速。碗状3-surfaces(双曲面、在普通几何)马克的连续的“节拍”相同的时钟。(这些3-surfaces类似球体闵可夫斯基的几何常数的表面的距离从一个固定的点)。我们注意到一个无质量的粒子,沿着光锥世界线运行以来,从未达到甚至第一碗状表面,同意以上说。

图2.22碗状3-surfaces马克连续相同的时钟“滴答”。

最后,测地线的概念,为一个类时曲线,大量粒子的世界线的物理解释在自由运动clo sychri clo sychri你好你好

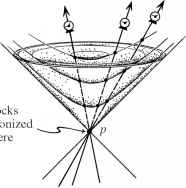
图2.22碗状3-surfaces马克连续相同的时钟“滴答”。

在重力。数学上,一个类时测地线l特点是任意两个点的事实在l p和q,相隔不远,最长的曲线(g)所提供的时间长度的感觉从p q实际上是l。见图2.23的一部分——好奇的逆转length-minimizing测地线欧几里得或黎曼空间的属性。测地线的概念也适用于零测地线,在这种情况下,“长度”为零,和null-cone时空结构单独能充分确定。这个null-cone结构实际上是相当于时空的保形结构,这将会对我们重要性。

图2.23类时测地线l特点是事实,对任意两个点p和q l,相隔不远,最长的地方从p, q曲线实际上是l的一部分。

类时测地线l类时测地线l

我\

继续阅读:黑洞和时空奇点

这篇文章有用吗?

+ 4 1