选定有机化合物的迟滞因子

材料延迟因子(Rd)

氯化1

氯仿3

四氯乙烯9

甲苯3

二氯苯14

苯乙烯31

氯苯35

(多氯联苯)可被大多数土壤有效去除。高可溶性化合物，如氯仿、苯和甲苯，即使是高有机土壤也不能有效去除。由于挥发和生物降解不一定取决于土壤类型，通过这些方法去除有机化合物往往在不同地点更加一致。表3.1列出了一些有机化合物的阻滞因子，这是根据几个文献来源估计的(Bedient et al.， 1983;Danel, 1953;罗伯茨等人，1980)。

3.1.2污染物移动

污染物随地下水的移动或迁移受前一节讨论的因素控制。这可能是池塘和其他水生系统以及利用慢速(SR)和快速渗透时需要考虑的问题土地处理概念。的地下区域如图3.1所示

国际扶轮盆地

国际扶轮盆地

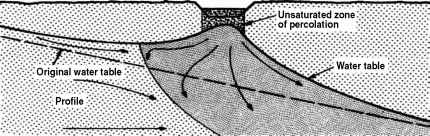
图3.1 SAT盆地的地下影响区。

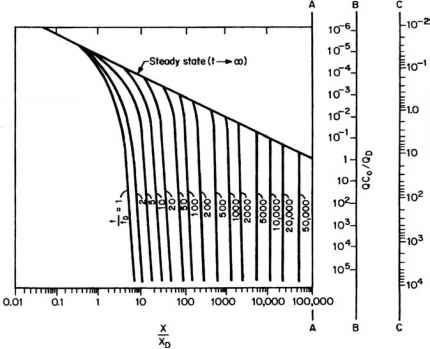
图3.2估算污染物传播的诺莫图。

对允许大量渗流的快速渗透盆地系统或处理池的影响。通常需要在源向下梯度的选定距离上确定地下水羽流中污染物的浓度。或者，可能需要确定给定浓度在给定时间发生的距离或给定浓度到达特定点的时间。图3.2是一个可用于估计下梯度羽流中心线上这些因素的诺莫图(USEPA, 1985)。上述讨论的分散和延迟因素包括在解决方案中。使用nomograph所需的资料包括:

含水层厚度， z (m)

渗流速度v (m/d)

分散性因子ax和ay (m)

延迟因子Rd为所关注的污染物

容积水流速，Q (m3/d)

污染源浓度，C0 (mg/L)

地下水背景浓度Cb (mg/L)

质量流量污染物QC0 (kg/d)

使用诺莫图需要计算三个比例因子:

Qd = (16.02)(n)(z)[Dx)(Dy)] (3.9)

这个过程最好用一个例子来说明。例3.1

测定烟柱中心线的硝酸盐浓度，600米下梯度快速渗透系统，系统启动后2年。资料:含水层厚度= 5 m;孔隙度= 0.35;渗流速度= 0.45 m/d;色散度，ax = 32 m, ay = 6 m;容积流量= 90 m3/d;渗滤液中硝酸盐浓度为20 mg/L;背景地下水中硝酸盐浓度为4 mg/L。

解决方案

1.下梯度容积流量结合了自然本底流量和SAT系统引入的额外水量。为了保守起见，假设在此计算中，烟羽起源处的硝酸盐总量等于指定的20 mg/L。然后将诺莫图测定的残留浓度添加到4 mg/L背景浓度中，以确定所关注点的总下梯度浓度。经验表明，当渗滤液通过土壤中的活性根区时，硝酸盐往往是一种保守物质，因此在这种情况下，假设阻碍因子Rd等于1。

2.确定离散系数:

Dx = (ax) (v) =(32)(0.45) = 14.4平方米/ d Dy = (ay) (v) =(6)(0.45) = 2.7平方米/ d

3.计算比例因子:

XD = DJv = 14.4/0.45 = 32 m tD = Rd (Dx) / (v) 2 = 1 (14.4) / (0.45) 2

Qd = (16.02)(n)(z)[(Dx)(Dy)]1/2

= (16.02)(0.35)(5)[(14.4)(2.7)]1/2 = 174.8 kg/d v

4.确定污染物的质量流量:

(问)(C0) = (90 m3 / d)(20毫克/升)/(1000克/公斤)= 1.8公斤/ d

5.确定nomograph的输入参数:

Xd 32

- = 10.3使用- = 10曲线tn 71 tn

Qd 174.8

6.在x/xD轴上输入值为18.8的nomograph，画一条与t/tD曲线= 10相交的垂直线。从这一点开始，在a - a轴上画一条水平线。在B-B轴上找到计算值0.01，并将其与之前确定的A-A轴上的点连接起来。将这条线延伸到C-C轴，读出关注的浓度，约为0.4 mg/L。

7.2年后，下梯度600m处硝酸盐浓度为诺莫图值与背景浓度之和，即4.4 mg/L。

必须使用适当的延迟因子对每种污染物重复计算。诺莫图也可用来估计给定浓度在给定时间内发生的距离。图上的线是很长一段时间内的“稳态”曲线，如例3.2所示，可用于评估达到平衡时的条件。

例3.2

使用例3.1中的数据，确定羽流中的地下水满足美国环境保护署(EPA)饮用水中硝酸盐的限制(10毫克/升)的下梯度距离。

解决方案

1.假设背景值为4毫克/升，则受关注点的烟羽浓度可能高达6毫克/升。在C-C轴上定位6mg /L。

2.将C-C轴上的点与B-B轴上的值0.01连接(如例3.1所确定)。把这条线延伸到A-A轴。从这一点画一条水平线与稳态线相交。将一条垂直线向下投影到x/xD轴，并读取x/xD = 60的值。

3.使用之前确定的xD值计算距离x:

3.1.3地下水堆垛

地下水堆垛示意图如图3.1所示。非饱和区渗流基本呈垂直流动，受Kv控制。如果在深部存在地下水位、阻碍层或屏障，则引入水平分量，地下水丘内的流量由Kv和Kh的组合控制。在土丘的边缘和更远的地方，流动通常是横向的，由Kh控制。

远离源的横向流动能力将决定将发生堆积的程度。可用于横向流动的区域包括地下含水层以及特定工程设计认为可接受的任何附加高度。过多的堆积会抑制SAT系统的渗透。因此，在土壤含水层处理(SAT)盆地中，地下水丘上方的毛细条纹与入渗表面的距离不应小于0.6米(2英尺)。这相当于地下水位深度约为1至2米(3至7英尺)，具体取决于土壤质地。

在许多情况下，卫星系统的渗滤液或羽流将作为基流出现在邻近的地表水中，因此可能有必要估计水源和出现点之间地下水位的位置。这样的分析将揭示在中间的地形中是否有可能产生渗水或泉水。此外，一些监管机构要求在土壤中有特定的停留时间，以保护邻近的地表水，因此可能有必要计算从源头到预期出现点的旅行时间。式3.10可用于估计水源向下任何一点的地下水位饱和厚度(美国环保局，1984年)。通常情况下，对多个位置重复计算，并将结果转换为高程并绘制在地图和剖面上，以确定潜在的问题区域:

式中h =非承压含水层在有关点(ft;米)。

h0 =源处无约束含水层饱和厚度(ft;米)。

d =从震源到关注点的横向距离(ft;米)。

Kh =土壤系统有效水平渗透性，中(ft/d)。

Qi =单位宽度的无承压含水层系统的横向流量

流量系统(ft3/d-ft;立方米/ d-m):

式中di =到渗流面或出水点的距离(ft;m). h =出水点无承压含水层饱和厚度(ft;米)。

横向流动的行进时间是水力梯度、行进距离、Kh和土壤孔隙度的函数，定义如式3.12:

tD =(Kh)(h0- h) (3'12)

式中tD =在地表水中横向流动从源头到出水点的旅行时间(ft;m). Kh =土壤系统有效水平渗透率(ft/d;m / d)。h0, hi =源、出口处无约束含水层饱和厚度，(ft;m). di =到渗流面或出水点的距离(ft;m). n =孔隙率，以十进制分数表示。

确定地下水丘的简化图形方法使用Glover(1961)开发的程序，并由Bianchi和Muckel(1970)总结。该方法适用于高于水平面、相当厚且假定有无限范围的均质含水层的方形或矩形盆地;然而，圆形盆地的行为可以通过假设面积相等的平方来充分近似。当地下水堆砌成为一个关键的工程问题时，建议使用Hantush方法进行进一步分析(Bauman, 1965)。由于地下水位倾斜或阻碍地下地层，导致“栖息”土丘或由于附近存在出口点，会出现进一步的并发症。对于这些情况，建议参考Brock(1976)、Kahn和Kirkham(1976)和USEPA(1981)的文献。简化的方法涉及图3.3、图3.4、图3.5或图3.6中几个因素的图形确定，取决于盆地是正方形还是矩形。

需要计算公式3.13到3.15中定义的W/(4at)05和Rt值:

12 =无量纲尺度因子(3.13)

式中W为补给池宽度(ft;米),

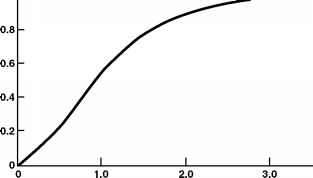
图3.3方形回灌盆地中心地下水丘形曲线。在哪里

Kh =含水层有效水平渗透率(ft/d;m / d)。

h0 =补给区中心下方含水层的原始饱和厚度(ft;m). Ys =具体的收益(使用图2.5或2.6确定)(ft3/ft3;m3 / m3)。

图3.3方形回灌盆地中心地下水丘形曲线。在哪里

Kh =含水层有效水平渗透率(ft/d;m / d)。

h0 =补给区中心下方含水层的原始饱和厚度(ft;m). Ys =土壤比产量(图2.5或2.6确定)(ft3/ft3;m3 / m3)。

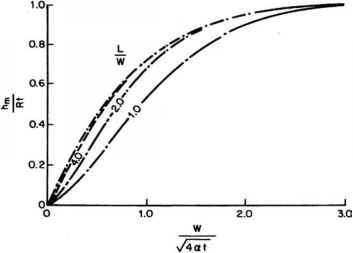
图3.4不同长宽比矩形回灌区中心地下水丘形曲线

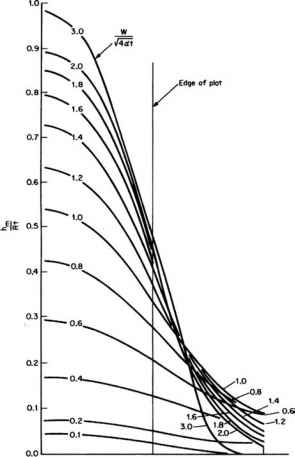
图3.5方形补给区下方地下水丘的上升和水平扩展。

图3.5方形补给区下方地下水丘的上升和水平扩展。

在哪里

R = (I)/(Ys) (ft/d;m/d)，其中I为单位面积土壤表面的入渗率或入渗水量(ft3/ft2-d;m3 / m2 / d)。t =浸润周期，d。

输入图3.3或图3.4中W/(4(at)1/2的计算值，以确定比值hm/(R)(t)的值，其中hm是土墩中心的隆起。使用之前计算的(R)(t)值来求解hm。可以使用图3.5(方形区域)和图3.6(矩形区域，其中L = 2W)

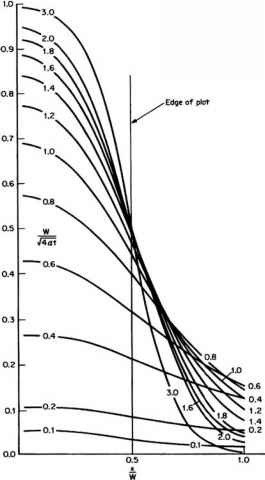
图3.6长宽两倍的矩形回灌区下方的地下水丘的上升和水平扩展。

估算距离回填区中心不同距离处土堆的深度。所涉及的过程最好用一个设计示例来说明。

例3.3

确定直径为30米的圆形SAT盆地下的地下水丘的高度和水平分布。原始含水层厚度为4 m，现场测定Kh为1.25 m/d。原地下水位顶部低于建成流域设计入渗面6 m。设计入渗速率为0.3 m/d，每循环废水施放期为3天(淹水3天，渗干10天;详情见第八章)。

解决方案

1.确定等效面积方形盆的大小:

则等效方形盆地的宽度(W)为(706.5)1/2 = 26.5 m。

2.用图2.5确定具体产量(Ys):

Kh = 1.25 m/d = 5.21 cm/hr Ys = 0.14

3.确定比例因子:

y 0.14

(4at)1/2 [(4)(35.7)(3)]1/2 0

(R)(t) = (2)(3) = 6 m利用图3.3确定因子hm/(R)(t):

hm = (0.68) R (f) = (0.68)(2)(3) = 4.08 m

5.原始地下水位低于入渗面6 m。计算得到的升高4.08 m将使丘顶距离盆地入渗面2 m以内。如前所述，这足以维持设计渗透率。如第八章所述，设计时可以考虑较短的淹水期(例如2天)，以在一定程度上减少堆垛的可能性。

6.使用图3.5确定土墩的横向扩展。使用W/(4(at)1/2的曲线和之前计算的1.28值，输入具有选定值的x/W(其中x是所关注的横向距离)的图形，并读取值hm/(R)(t)。求出从盆地中心线到土丘顶部10米的深度:

用这个值输入x/W轴，投影到W/(4at)l1/2 = 1.28，然后在hm/(R)(t)轴上读取0.58:

10米处的土墩深度为6米- 3.48米= 2.52米。同样地，在x = 13 m时，到土丘的深度为3.72 m，在x = 26 m时，到土丘的深度为5.6 m。这表明水位在大约等于两倍流域宽度的横向距离上几乎恢复到正常地下水位。将施水时间从3天改为2天，可将峰值水位降低到盆地渗透面以下约3米。

例3.3中演示的程序对单个盆地有效;然而，如第八章所述，SAT系统通常包括多个按顺序加载的盆地，通过假设整个处理区域在设计时均匀加载来进行堆丘计算是不合适的液压加载速率．在许多情况下，这将导致错误的结论，即堆积将干扰系统操作。

首先，有必要计算单个盆地下的土丘在洪水期间的上升。当水力加载在时间t停止时，假设均匀的假设流量从时间t开始，并持续到剩余周期的平衡。这两个土丘高度的代数和就近似于下一个洪水期开始前的土丘形状。由于相邻的盆地可能在同一时期被淹没，因此也有必要确定其土丘的横向范围，然后加上这些来源的任何增量，以确定有关盆地下的总土丘高度。该过程由例3.4说明。

例3.4

在操作周期结束时，确定SAT盆地下的地下水丘高度。假设这个盆是方形的，边长26.5米，是四个盆中的一个，排成一排(宽26.5米，长106米)。假设现场条件与例3.3相同。还要假设，一旦有关盆地的休止期开始，其中一个相邻盆地就开始发生洪水。运行周期为2天放水，12天休息。

解决方案

1.有关盆地下的最大上升高度与例3.3中2天淹水计算的结果相同:hm = 3.00 m。

2.未来2天洪水对邻近盆地的影响约等于例3.3中计算的26 m点的土丘隆起，或0.4 m。所有其他盆地都在影响范围之外，因此关注盆地下方的最大潜在上升为(3.00)+ (0.4)= 3.4 m。土丘实际上不会升得那么高，因为在这两天里，邻近的盆地被淹没了，第一个盆地在排水。然而，为了计算的目的，假设土丘将上升到静态地下水位以上3.4米。

3.这种“均匀”放电的R值将与例3.2中计算的R值相同，但t现在将是12天:(R)(t) = (2)(12) = 24 m/d。

4.计算一个新的W/(4at)1/2，因为“新”时间是12天:

W/(4at)1/2 = 26.5/[(4)(35.7)(12)]1/2 = 0.62

5.用图3.3确定“hm”/(R)(t) = 0.30:“hm”= (24)(0.3)= 7.2 m。这是假设在10天休息期间，土丘可能会发生的下降;然而，水位实际上不可能下降到静态地下水位以下，因此最大可能的下降将是3.4米。这表明，在下一次洪水周期开始之前，土丘就会消散。假设沉降以0.72米/天的均匀速率发生，3.4米高的土墩将在4.7天内消失。

如果地下水堆积分析表明系统运行可能受到干扰，则可以采用几种纠正方法。如第八章所述，可以调整浸水和干燥循环，或将盆组的布局重新安排为盆间干扰较少的配置。最后一种选择是减少场地排水，从物理上控制土丘的发展。

当浅层或季节性自然地下水水位可能干扰陆地或水处理系统的运作时，也可能需要排水不足来控制它们。地下排水系统有时也用于回收土地处理系统下处理过的水，用于有益的使用或排放到其他地方。

3.1.4地下排水

为了有效，排水或水回收元件必须在天然地下水位或在天然地下水位内，或刚好在某些其他流动屏障之上。当排水管可以安装在5米(16英尺)或更低的深度时，下排水管比一系列井更有效，成本更低。采用现代技术，可以通过一台机器切割然后关闭沟槽，在土工布膜中安装半柔性塑料排水管。

在某些情况下，为了控制浅层，下排水是一项必须的工程地下水的表因此，该场地可以开发用于污水处理。这种排水渠如果对地下水控制有效，也会从土地处理作业中收集经过处理的渗滤液。收集的水必须排放，所以在这种情况下使用地表水排放系统，除非水以其他方式使用或处理。在一些情况下，已经安装了排水管来控制季节性的高水位。这种类型的系统可能

液压加载机械Lw + P

雷竞技csgo11111111111

土壤表面

继续阅读:生化需氧量的去除

这篇文章有用吗?

0 0