离心力
在本节中,我们推导出的表达式离心力的身体朝着一个圆半径与角速度Q,如图3.5所示。
圆周运动的加速度
让我们首先考虑什么力量参与身体运动和匀速圆周运动。牛顿第一运动定律说,如果身体是留给自己的设备,它将保持静止或匀速直线移动。如果身体正在匀速圆周运动(例如,一个孩子骑在旋转木马,或者更多的把对我们来说,一个人站在地球旋转地球的轴每天一次),那么,身体必须加速,加速朝向旋转轴。
让我们假设在一个小时间,圣,身体穿过一个小角,所以角速度是X = /圣。身体的速度是一个常数,
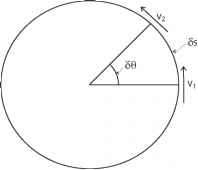
图3.5。身体朝着一个圆是不断变化的方向,所以加速。加速度是指向圆心,v2 / r级,v是身体的速度和r是圆的半径。
图3.5。身体朝着一个圆是不断变化的方向,所以加速。加速度是指向圆心,v2 / r级,v是身体的速度和r是圆的半径。
v = rX = r 50/5t,但其方向是变化的,这样,运动的方向是垂直于半径;因此,如果在最初的时间位置向量r1,那么它的速度,v1,在垂直方向上,和一个短的时间后,速度v2垂直于它的新位置向量,r2。
我们可以看到在图3.5中,半径矢量的角度已经感动的距离有关
因为速度总是垂直于半径,速度的方向必须通过相同的半径和角度
身体的加速度等于速度的变化率;使用方程3.14,我们获得
在过去的平等使用v = r86/8t的事实。也就是说,身体处于匀速圆周运动的加速度是圆的半径和向其中心和级v2, r = = X r。(3.16)
这种被称为心加速度,和相关的力导致加速度(必须有一个力)向心力和向内,向旋转轴。
部队在旋转参照系
现在让我们考虑运动从一个观察者的角度接受匀速圆周运动。考虑一个启发性的例子是在绕地球轨道卫星和空间站;当一名宇航员太空行走的空间站,她似乎是轻便,没有任何力量作用于她(图3.6)。现在事实上,宇航员地球周围正在进行圆周运动,因此加速,提供加速度是地球的重力。
一)固定或惯性坐标系

^ - b)旋转参照系中重力
离心力
图3.6。宇航员绕地球。面板视图的运动在一个静止的参照系,地球的万有引力提供向心力,使宇航员地球轨道。面板b视图的情况从宇航员的参照系,引力是完全平衡离心力和宇航员感觉轻便。
但从一个观察者的角度旋转的宇航员,宇航员是静止的,因此没有合力作用于她。现在我们知道重力是演戏,把她扔向地球,和我们说由另一个力,这个力是平衡离心力,推她出去。力完全平衡,所以宇航员出现失重;在旋转坐标系,向心引力把她扔向地球就是平衡离心力推她出去。因为向心力大小X2r,离心力也必须有这个大小,我们得出这样的结论:在旋转参照系中,似乎有一种额外的力量,离心力,以起到加速身体沿着半径,从轴向外旋转。离心力的大小是每单位质量X2r,其中r是转轴的距离。
没有离心力在惯性参考系。然而,考虑到我们生活在一个旋转的星球上,非常方便描述地球上的运动从一个旋转参照系中,地球表面是静止的,在这个框架看起来有一个离心力,试图进入太空。更幸运的是我们这些生活在地球的表面,离心力比地球引力弱得多。
继续阅读:WiNDDRivEN循环和伟大的环流
这篇文章有用吗?