生化需氧量
D 10/300
2.1.15硝化在BOD测试
在含耗氧成分的废物的BOD测试中耗氧的大致情况见图2.1。如前所述,由于硝化菌不能轻易与碳质细菌竞争,它们需要大约5天左右的时间才能发育。因此,大约5天后,曲线突然上升,由于氮氧需求量, NBOD。然而,如果在试验开始时硝化剂含量丰富,则可在短滞后后立即施加氮部分,如虚线所示。该图显示了抑制硝化的必要性,如果碳质氧需求, CBOD,是BOD测试中所需要的。
反应在硝化过程由两种自养细菌介导:亚硝化单胞菌而且硝化菌属.氨来自任何有机物质的氮含量,如蛋白质,含有约16%的氮。一旦氨从有机物中被水解,亚硝基单胞菌就会消耗它,在这个过程中也会消耗氧气
-
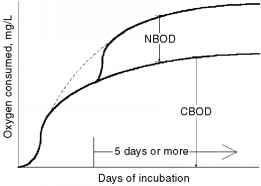
- 图2.1 CBOD和NBOD的发挥。
以下反应:
■- nh + + J^O ^——NO- + 4-H+ + e- (2.3)
:- o2 + H+ + e-^ 2-H2O (2.4)
添加方程式。(2.3)和(2.4)产生j-NH + + J-O2 ^ I-H2O + 1无效- + 3 - h + (2.5)
式(2.4)称为电子受体反应。式(2.3)为选子供体反应,即为电子受体反应提供电子。这两个反应一起为亚硝基单胞菌产生能量。
方程(2.5)中产生的NO-是另一种细菌——硝化杆菌的电子源。硝化杆菌使用亚硝酸盐后的化学反应如下:
-NO- +——H2O ^——NO- +;- h + + 1e- (2.6)
与亚硝基单胞菌一样,先前的反应一起提供了亚硝基杆菌所需的能量。联合反应的破坏铵离子, NH+,(或氨,NH3)可通过加入等式得到。(2.5)和(2.8)。这将产生
1nh4 ++ io2 ^ 1-no -+ i.h2o + 3h + (2.9)
由式(2.9)可知,1.0 mg/L NH4-N相当于4.57 mg/L溶解氧。
2.1.16生化需氧量实验室数据的数学分析
将潜伏期持续5天以上至20至30天,可获得最终碳质氧需要量。要做到这一点,应通过在培养瓶中添加适当的化学物质来抑制硝化剂。另一种获得CBOD的方法是通过数学分析。
在孵育过程中,设y为任意时刻t的累积耗氧量(摄氧量),设Lc为原始废弃物的CBOD。氧累积量的累积速率dy/dt与剩余的CBOD消耗量Lc - y成正比,因此,ddyy = y = kc(Lc - y) (2.10)
其中kc是一个比例常数,称为脱氧系数。
在前面的方程中,如果将kc和Lc的正确值代入,则方程左边应该等于方程右边;否则,剩余R将满足
在每个相等的时间间隔内,可以确定y的值。对于n个区间,y也会有n个值,每个区间对应的Rs可以是正的也可以是负的。如果将这些r加起来,结果可能是零,这可能会给人留下残差为零的印象。另一方面,如果残差是平方,总和的结果总是正的。因此,如果平方和等于零,那么残差实际上等于零是没有歧异的。
y的n个值对应于时间t的n个值其中包含一个kc值和一个Lc值。由式(2.11)可知,这些值可以通过偏微分得到。根据前面的段落,当R的平方和等于零时,可以确定残差为零。这意味着当平方和为零时,平方和的偏导数也必须为零。因此,R对kcLc和kc的和的偏导数为零。因此,为了得到kc和Lc,平方和的后一个偏导数必须等于零来强制解。刚才描述的方法被称为最小二乘法,因为使偏导数等于零等于求最小二乘。推导出相应的方程如下:
继续阅读:信息Dct
这篇文章有用吗?
