O2 hv O3P O3P750
原子氧处于基态。这种赫茨伯格解离连续体很弱,从185 nm延伸到242 nm,是地球大气中海拔低于60 km的O原子的主要来源。的吸收截面图7.4给出了O2随赫茨伯格连续统波长的函数。
核间距离(埃)
核间距离(埃)
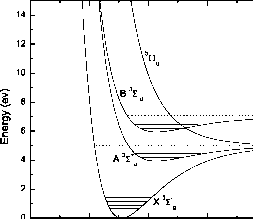
浮动。7.3.O2和振动-旋转能级的理想势能曲线,解离极限在7.047和5.080 eV。
从x到B3£-的束缚跃迁涉及到不稳定排斥态5n”、3n”、1n”和23S+的非辐射跃迁,导致预抛离。这是一个允许的强舒曼-朗格带系统,在175到200 nm之间具有尖锐的带结构,导致激发态O(1D)中的一个氧原子的解离通道。吸收截面具有详细的振动-旋转带结构。图7.4给出了横截面的平均值。在舒曼-龙格带中,主要是在60 - 90千米之间通过吸收分解O2。
从X3Sr到B3£的解离连续谱的束缚连续谱跃迁也产生了与舒曼-朗格带相同的原子氧产物。这种跃迁导致在137和175 nm之间产生强烈的舒曼-朗格解离连续体。截面峰值在142.5 nm处,如图7.4所示,在129.4 nm、133.4 nm和135.4 nm处有三个弥散带(离散态和连续介质之间的相互作用)。舒曼-朗格连续介质中的吸收是90 km以上的主要氧解离过程。
赫兹伯格和舒曼-朗格两个连续体的一小部分位于舒曼-朗格带之下。Nicolet和Kennes(1986)给出了
Schumann-Runge连续
舒曼-朗格连续体
0.24
波长(nm)
波长(nm)
0.24
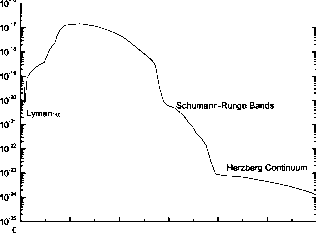
7.4浮动的。O2在273 K时的吸收截面(带结构已平均)。
赫茨伯格连续介质截面a(x) = 7.5 x 10 4xexp-50 (lnx)2],
其中x = 199/A, A单位为nm,建议在210 nm以上使用。舒曼-朗格带的横截面随波长变化很大,这是由于数千条重叠的旋转线被预解离和多普勒展宽而加宽,从而产生福格特旋转线轮廓。带截面是温度依赖的,因为温度影响基态振动和旋转能级的总体,它也影响单个旋转线的展宽。因此,很难给出用于模拟大气光化学的波长间隔的平均横截面。在波段峰值之间具有波长的光子可以深入大气层,因为其截面可以在20厘米-1或10-5纳米的区间内变化两个数量级。Murtagh(1988)使用高光谱分辨率截面,推导出17个宽光谱区间(175.4至205.8 nm)的平均截面,并以O2柱数密度(分子cm-2)为函数表。Allen和Frederick(1982)给出了17个宽光谱区间的截面温度依赖表达式,用于光化学建模研究。
在137 nm以下,太阳莱曼-a线对O2的光解起着重要作用。横截面与温度有关,并且在莱曼-a线上变化显著,几乎相差一个数量级(图7.4)。Lewis等人(1983)在温度为84、203、288和366 K时,将波长区间121.40到121.90的截面制成了表格,间隔为0.01 nm。我们记得太阳的莱曼-a通量在太阳周期中以2倍的倍数变化。
O2的光离极限为102.78 nm。光离产率在60 nm以下为1,在102.57 nm处为0.65,对应Lyman-,3。137 ~ 105之间的截面高度结构化,在10~20 ~ 10~17 cm2之间变化,而在100 nm以下存在电离连续体。对于光化学建模,在较宽的区间内获得平均截面是有用的,为此目的,Banks和Kockarts(1973)将102.57、97.7(对应于太阳C(III)双电离碳线)的吸收和光离截面以及91至8 nm的7个光谱区间制成表格。在71.9 nm以下,当第二通道在60 nm以下时,解离光离是可能的。7.6.4 O3光解作用
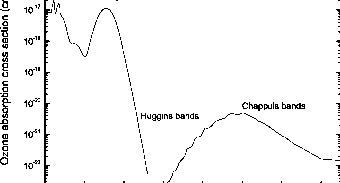
臭氧在200到300纳米波长范围内吸收较强。从300到350 nm,它吸收在相对较弱和温度依赖的哈特利带。它还吸收在Chappuis波段410和850 nm之间的可见区域。臭氧的光解阈值为1.14 ^m。臭氧是云层上方太阳紫外线和可见辐射的主要大气吸收体,因此增强因子fx(如图7.2所示)的变化与臭氧吸收截面(如图7.5所示)的变化成反比,在0.3 ~ 0.75 × m之间。在0.3℃以下,哈特利波段的强烈吸收导致对空间没有反射辐射,因此fx = 1。fx在0.6′时的最小值对应于臭氧可见Chappuis波段吸收截面的峰值。根据光子波长的不同,臭氧可光解成不同的产物(见附录B,表B.3)。
生产O(1D)的量子产率对于330 nm的>可以忽略不计,但是对于A < 306 nm的量子产率在310 nm附近迅速上升到0.9,与温度无关(喷气推进实验室2006)。
赫恩(1961)报告了在哈特利波段253.7、289.4、296.7和302.1 nm波长的绝对测量。特别是Hearn (1.147x10~17 cm2分子-1)的253.65 nm截面
O2(3如)+高压^ + + O (3 p) + e, O2(£3 -)+高压^ + + O + e (XD),
-
- 波长(urn)
7.5浮动的。臭氧从莱曼-a到可见光的吸收截面,在273 K(带结构已平均)。
国际机构的首要标准。这些结果已作为规范涵盖整个地区的相对测量的基础光谱。吸收间隔175.4至362.5 nm的截面在JPL(2006)中为273 K制成表格。同时给出了在305 ~ 320 nm之间O(1D)产率随温度变化的量子产率表达式。Bass和Paur(1981)测量了截面的温度依赖性,发现在263 ~ 350 nm区域温度依赖性显著,主要对应于Huggins带。查普伊斯带的原始测量是由Vigroux(1953)完成的,后来由Griggs(1968)验证。
7.6.5 H2 O光解
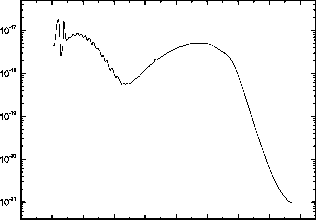
水蒸气的吸收截面如图7.6所示。水蒸气可被波长低于246纳米的光子光解离。在145 nm以下有三种可能的通道
H2O + hv - H2 + O(1D), H2O + hv - 2H + O, H2O + hv - H + OH,
-
- 110 120 130 140 150 160 170 180 190 200波长(nm)
7.6浮动的。水在296 K时的吸收截面。
其中第一和第二通道的分支比a = 0.11,第三通道的分支比a = 0.78。这些通道主要由莱曼-a光子产生。当T = 292 K时,Lyman-a区间121.48-121.64 nm上的平均吸收截面为1.55x10~17 cm~2。在145nm以上,水蒸气按照第三通道光解。根据Yoshino et al.(1996)和Parkinson and Yoshino(2003)的测量结果,296 K时H2O的吸收截面如图7.6所示。
7.6.6 CO2光解作用
在图7.7中,我们根据Lewis和Carver(1983)的高分辨率(0.005 nm)测量,显示了从Lyman-a到约0.2±的CO2的温度依赖性吸收截面。Jensen等人(1997)也证明了这种温度依赖性,他们给出了在高温(1000 K以上)下,光谱范围为0.19 ~ 0.32′的温度依赖性吸收截面。在0.200 ~ 0.206 ×之间,Karaiskou等人(2004)给出了295 K和373 K的吸收截面测量值。
根据这两个通道,CO2在0.2275℃以下光解
CO2 + hv CO + O(3P) 0.2275 >A> 0.1672′,(7.60)CO2 + hv - CO + O(1D) A < 0.1672′。(7.61)
-

- 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20波长(nm)
图7.7。对CO2在199 K、294 K和368 K的吸收截面(低温时的能带结构)进行了平均。
第一通道的量子产率统一到约0.21 pm (Okabe 1978)。最重要的区域在0.14-0.18 pm之间,对应于分子氧舒曼-朗格带和连续介质的吸收区域。
7.6.7 CH4光解
甲烷在波长小于145 nm处吸收强烈,并根据以下重要通道进行光解解
对于Lyman-a,第一通道的分支比为0.24,第二通道为0.25,第三通道为0.51。在Lyman-a以上,第三通道的分支比为一。图7.8显示了不同来源甲烷的吸收截面。37.43-91.11 nm区域的数据来自Samson等人(1989),38.0-18.0 nm区域的数据来自Lee等人(1977),在Lyman-a Brownsword等人(1997)给出的平均值为(2.0±0.1)x!0~17 cm~2,而
CH4 + hv ^ CH2 +H2, CH4 + hv ^ CH2 + 2H, CH4 + hv ^ CH3 +H。
0 10
0 10
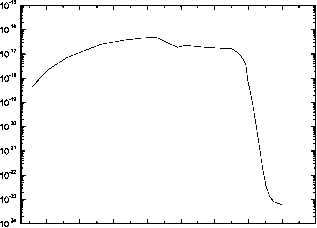
7.8浮动的。室温下CH4的吸收截面。
137-160 nm的数据来自Mount等人(1977)。Lavvas等人(2007)给出了其他截面数据、光解途径及其相应的分支比的进一步参考。
7.6.8大气光解速率
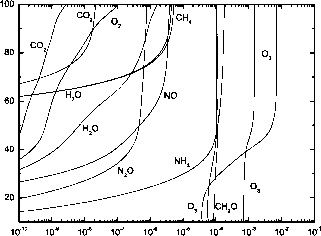
附录B表B.1至B.3给出了全球平均条件下,在大气顶部紫外线和可见光谱区域太阳辐照时大气物种总的光解离和光离率的典型值。图7.9显示了全球平均大气条件下各种分子随高度变化的光解速率。
对于前面提到的与图7.2有关的全球平均条件,给出了两个通道的臭氧光解速率随海拔的变化。第2通道在40 km以上显著,TOA光解速率为7.1 x10~3。第一个通道在40 km以下显著,TOA速率为1.5x10~3 s_1。在上层大气中,二氧化碳的第二个通道是重要的,而在平流层中,第一个通道是重要的。由于CO2截面在0.167 pm以下的温度依赖性,在TOA时第二通道的光解速率增加到7.45x10~7 s_1。如图所示,大气中70公里以上的太阳莱曼-a线和70公里以下波长大于莱曼-a的光子主要使水蒸气分离
-
- 光解速率(s1)
7.9浮动的。对于全球平均大气条件,各种重要分子的光解速率随海拔的变化。
7.7碰撞诱发反应
7.7.1反应类型
让我们考虑一个由两个原子a和B组成的双原子分子,这个分子通过碰撞被激发到更高的能态AB*。然后,分子可以通过单分子反应自发分解成其组成原子
分子AB可以通过双分子反应与第二分子或催化分子M碰撞解离成其组成原子
或者,在双分子反应中,两个原子A和B可以发生结合反应形成分子AB
组成原子与催化分子M之间的碰撞可导致三分子重组反应
涉及四个或更多分子的碰撞是非常罕见的。
7.7.2双分子反应
对于由碰撞驱动的双分子反应,我们可以根据简单碰撞理论定义分子间每单位体积每秒的双分子碰撞率zab = ZoUAUB (7.69)
在哪里
其中的单位为cm3分子-1 s-1,其中的平均分子速度由eqn给出(7.15),¿aB是碰撞分子的平均直径,如eqn(7.16)。碰撞率,Zab的分子单位为cm~3 s_1,用于碰撞分子的总体。它随\/T变化,与实验不一致。原因是分子反应的速率远小于分子碰撞的速率。为了使反应继续进行,反应物a和B必须形成过渡态AB*,其势能高于反应分子或反应物或生成物C和D
为了使反应向前进行,反应物需要活化能,Er,来形成过渡态。同样,生成物需要活化能Ep,才能形成逆向反应的过渡态。
分子A每立方厘米每秒的破坏率与反应分子的密度的乘积成正比。这就是质量作用定律,可以用数学形式写成速率方程
= -kfnAnB, (7.72)
dt,其中比例常数,kf在cm3分子中-1 s-1,是正向速率常数,与分子b的破坏方程相似。反应的正向速率常数,和反向反应的速率常数kb,通过平衡常数K联系起来,由
继续阅读:T [M
这篇文章有用吗?



