Radiationtransfer理论
3.1介绍
生产辐射的身体周围通常从本质上是黑体表面或表面热辐射的吸收大部分事件。行星大气通常是理想的黑体,除非它们包含大量的吸收分子。表面或发出的辐射大气层经历吸收和/或散射、大气的分子构成,它通过大气传输。非常大的距离辐射也稀释了辐射源周围空间增大,根据平方反比定律。吸收和发射表面的投影面积发生表面的方向辐射。因此,行星吸收太阳辐射基本上作为阀瓣和释放出热红外辐射一个球体。
从黑体发射的普朗克定律所描述的,维恩和斯蒂芬玻尔兹曼。第一个给出了光子的光谱分布,第二的位置最大发射波长和第三给的依赖对温度的辐射的总量。随着温度的增加,光子在逐步更高的能量释放。在行星大气层,因此自然排放限制所有波长的红外线而吸收可能发生从伽马射线到无线电波。热红外辐射我们需要包括吸收和发射的辐射传输方程。的我们只包括太阳辐射吸收和散射由大气分子和粒子(云、气溶胶)。
我们现在一些简单经典求解辐射传输方程的方法,这些方法形式获得的基础和理解行星大气中的辐射场。
3.2基本定义
3.2.1平方反比定律
让我们假设一个虚拟的中心的面积范围有一个无限小的身体,向四面八方辐射各向同性的。然后,发出的总辐射的一部分转移到一个元素
-
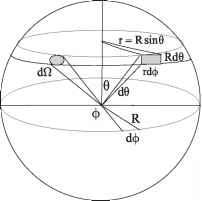
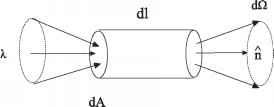
- 图3.1。辐射范围半径为R, 6天顶角,方位角度0,杜小圆半径R,立体角的元素。
面积达的dA /是一个范围。发射的辐射可以被视为组成的小的锥形束光线锥的底部有一个元素的面积大。辐射包括立体角的锥,d ^,以球面度(sr)和由dl =罪dddd ^,
0天顶角和方位角,美元在图3.1中定义。在极地坐标,极轴定义了天顶距,而赤道轴定义了方位角。球的半径为R,而小的圆球面上的元素用R。面积哒然后由哒= (rd)美元(Rd0) (3.2)
因此dA =罪R2 0美元d0d这球的总面积是c 2 n c n
因此总辐射传输的分数通过dA dA给出1 d ^, s
因此,表面的辐射范围可分为单位球面度总4 n (sr)对整个球体。
-
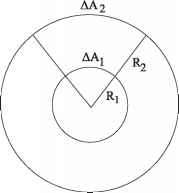
- 浮动。3.2。平方反比定律,基于一个发射中心半径范围Ri和接收R2的半径范围。为每个领域也显示面积元素。
R2虚拟的半径范围的中心让我们放置一个球面半径R1的身体散发出等效全向的辐射,向各个方向,见图3.2。然后从一个元素发出的辐射面积AA1中央球事件的元素的外部虚拟球表面积AA2, AA2 > AAi的地方。如果发射光子的数量单位面积是守恒的立体角内∠AA1 AA2,然后在一个单位面积的辐射距离R2虚拟球面的中心是根据比例稀释
3.2.2光辉
单色辐射,我\被定义为(J)发出的能量通过一个元素或转让区5 (m2)的方向定义的单位向量在一个元素的立体角d n ^ (sr)每秒(s)在一个波长间隔SA在¡m如果波长测量单位的光辉
我们包括下标波长上区别于发光元件的尺寸的区域。如果我们表示的方向垂直于无穷小元素的区域,采取平面,由单位向量k,然后元素的投影面积的方向辐射是SA (k•n)。因此,减少了投影面积的辐射方向走向地平线根据cos 0, 0是角的地方
-
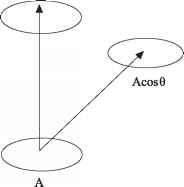
- 图3.3。发光区域的投影方向,使得正常的一个角6。
之间的垂直方向和辐射的方向,见图3.3。释放的总能量(J)或转移通过区域的元素n是方向
在一个时间间隔内圣,在光谱间隔SX,立体角内Sl。
3.2.3意味着光辉和通量
单色的意思是光辉的一个点在空间r的定义是光辉在各个方向根据平均
1 f J
老4 n J m2•s••jmx
单色的辐射通量(或辐照度)是通过一个元素发出的光辉或转移的区域,5,位于一个点平均r在四面八方,占的投影面积根据外汇(? t) = j >第九(r n t) cosddQ (3.9)
和单位W m ~ 2 m ^ ^ 1。我们可以执行上述积分使用eqn(3.1)来表达迪勒在极地坐标和设置¡j = cos 0
2 n - 1
我们注意,如果辐射各向同性然后消失的积分区域的一个元素就是转移辐射,如在一个气氛,和我们没有净通量穿过区域。如果我们有一个表面发射isotrop-ically上半球,然后积分降低h (? t) =倪\ (r, t), (3.11)
在n球面度单位。我们可能将对所有波长的单色通量获取总通量(或总辐照度,W m ~ 2)发出一个表面f (r, t) = n第九(r, t) d \。(3.12)
大气中的一个元素的总通量事件获得的体积是集成在球体周围的f (r, t) = 4 n第九(r, t) d \。(3.13)
3.2.4光度
元素的单色光度Lx,表面积发射或转移辐射,是单色通量乘以面积根据
Lx第九(r, t) = J (r n t)股价因为OdQ (3.14)
为一个元素放射出的辐射均匀或转移的区域
Lx第九(r, t) = SA J (r n t) cos0dQ (3.15)
和总光度,L,各向同性的辐射
对于一个发射球面半径为R的总表面光度
3.3黑体辐射
黑体被定义成为一个完美的发射器和吸收器。完美的黑体固体表面或完全不透明的大气层,辐射各向同性和排放是均匀的整个表面区域,表现为均匀的表面温度T (K)。与一个行星或恒星absorbing-emitting-scattering大气空间的辐射可能不是最理想的黑体辐射。
3.3.1普朗克定律
理想黑体的辐射是由普朗克函数,在波长方面
其中c是光速在真空中,h是普朗克常数和h是Boltz-mann常数。的频率(v = c / A)的形式
我们注意到普朗克函数的两种形式是相关的
这表达了事实,释放出的能量每单位面积上的老年代在相同的能量间隔相同。
3.3.2斯蒂芬玻尔兹曼定律
发出的总通量(W m - 2)黑体是由eqn(3.12)通过取代光辉普朗克函数f (T) = W BX (T)哒。(3.21)
设置hc / AkT = y和整合我们的积分等于n4/15,使简单的结果f (T) = aT4 (3.23)
被称为斯蒂芬玻尔兹曼法,其中一个是斯蒂芬玻尔兹曼常数
等于5.67 x10 J ~ 8 m ~ 2 K-4 s - 1。对于一个恒星或行星我们可以分配一个有效的黑体温度、画眉草,这样的总光度的身体
R是其半径。
-
- 35 0 5 10 15 20 25 30 40 45 50波长(| jm)
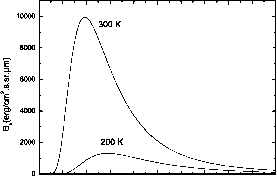
浮动。3.4。普朗克函数与波长和温度的变化。
3.3.3辐射能量密度
辐射通量守恒的连续性,可以表示为密度通量(W m ~ 2) = (J / m3) x速度(米/秒),(3.26)
在黑体光子通量成一个元素周围的球体的体积是4 aT4因此辐射密度,e
3.3.4维恩位移定律
普朗克函数与波长和温度的变化见图3.4。波长,A *¡m,对应的最大发射辐射,根据维恩黑体温度成反比定律
2898年
* = T (K)•< 3-28 >
的波长*是条件,dB \ (T) / dA = 0。随着黑体温度的增加,光子在更高的能量变得更多,因为光子能量高压= hc /。普朗克函数的峰值波长移动到更高的温度降低,我们注意从图3.4,普朗克函数在较低的温度总是低于在更高的温度。我们也注意到快速增长在普朗克函数的峰值
辐射 |
Aa - A6(/生病) |
T (K) |
能级跃迁 |
Y-rays |
1 (T6 - 1 (T4 |
10« |
核 |
x射线 |
身手_ IQ-2尤其 |
106年 |
内部电子 |
紫外线 |
0.39 10 - 2 _ |
104年 |
外部电子 |
可见 |
0.39 _ 0.75 |
103年 |
外部电子 |
似乎红外 |
0.75 _ 5 |
103年 |
分子振动 |
红外线 |
5 _ 40 |
102年 |
分子振动 |
far-infra-red |
400 _ |
10 |
分子旋转 |
微波 |
400 _ 104 |
10 - 1 |
分子旋转 |
无线电波 |
104 - 107 |
1 (T4 |
自旋反转 |
与温度。表3.1给出了类型的辐射其生产和相应的典型的黑体温度。
3.4吸收、发射和散射
大气分子吸收、发射和散射辐射。粒子云水滴或冰晶和气溶胶等(灰尘的各种化学成分包括水)在辐射转移也起着重要的作用。在散射过程中,一个光子可以改变其方向和波长。行星大气吸收和再发射波长相干,是散射粒子。散射过程中起着重要作用的转移太阳辐射通过行星大气层通过改变光子的方向。氛围可能物理深度但对于光子的物理深度除以平均自由程吸收和散射决定之前通过大气传输。
3.4.1吸收和发射
我们定义吸收的过程一个粒子(电子,原子或分子)与光子相互作用产生的光子能量转移大气中含有的热能粒子。逆过程排放。这个过程允许能量从一个大气的一部分沉积在另一部分,可能在光学方面。这能量转移层之间的气氛已经暗示系统没有关闭,所以充其量只局部热力学平衡(LTE)可以获胜。严格的热力学平衡(TE)需要关闭系统的外部环境。我们将讨论TE的概念,LTE和non-LTE在后面的部分。
吸收和发射过程的例子包括:
光致电离,或束缚自由电子转换,即光子被原子吸收导致自由电子。光子能量是由自由从它所需要的能量束缚态原子内剩下的能量要电子的动能。光致电离也可以发生在阶段,即一个电子首先兴奋地更高的束缚态电离能限制以外的碰撞激发紧随其后。自由电子可以接受光致电离的逆过程,辐射复合,通过光子的发射,其捕获原子束缚态。这个过程排放导致大气被转化为热能辐射能量。
束缚束缚电子转换碰撞去激发紧随其后。电子兴奋到更高的能级,被电离限制最高,其次是与另一个粒子碰撞的原子导致初始光子能量的转移热能的气氛。逆向过程辐射去激发,落在一个较长的束缚态电子通过一个光子的发射。
免费电子转换即自由电子吸收一个光子和改变它的轨迹相对于离子,进一步从离子。这实际上是另一个例子photon-particle所需的改变在一个电偶极子相互作用。结果是,电子加速,因为它获得了能量。这是量子力学的结果,因为传统加速电荷释放光子。相反的过程是免费排放或轫致辐射,即电子减速沿着它的轨迹相对于离子的出现作为一个光子的能量损失。
3.4.2散射
我们定义散射光子的过程,通过其与另一个粒子,可以改变其能源或方向,或两者兼而有之。如果光子的能量并不明显改变我们参考photon-particle交互作为弹性与微不足道的能量转移到大气的热能。
弹性散射过程的例子包括:
再分配散射,束缚电子是photo-excited更高的束缚态紧随其后的是辐射去激发回到原来的绑定状态。发出或即将离任的光子能量可能经历了一个变化和方向相对于吸收或传入的光子,但能量变化是微不足道的。这本质上是弹性散射,因为能量差起源于电子束缚态的扩散或扩大不离散能量状态。如果他们,那么再分配散射是一致的,即入射光子能量和即将离任的光子能量是相同的。然而,这通常是一个小电子束缚态允许能量扩散等扩大机制由于自然、多普勒或碰撞,这将在后面一节中讨论。再分配的一个极端的例子散射是荧光,光子被原子吸收导致更高的束缚态电子兴奋之后,辐射去激发与发射阶段到一些低水平的几个低能量的光子入射光子。
瑞利散射,光子与一个相对较小的粒子,如一个原子或分子,仿佛散射光子的粒子是一个固体粒子发生反冲。光子能量的散射过程是一致的,但方向是修改。对小的波长散射变得更有效。
米氏散射,即一个相对较大的粒子,如水滴或尘埃粒子,光子散射方向不同,其在光子能量的入射方向不改变。
汤姆逊散射,光子和电子相互作用电子发生反冲。这通常适用于光子能量较低,低于x射线。
非弹性散射过程的例子包括:
康普顿散射,高能(x射线和上图)光子与电子相互作用,发生反冲。photon-scattering过程从而不连贯的和即将离任的光子能量明显不同(低)的传入的光子。
极高的逆康普顿散射,电子能量(rel-ativistic)与光子相互作用和转移其光子能量的一部分。即将离任的光子也因此大幅增加能源,例如一个紫外光光子转换成一个x射线光子。
3.4.3的消光系数和光学深度
让我们考虑一个元素包含粒子的体积V(图3.5)各有一个有效截面积年代\,吸收和散射光子的波长A .然后我们定义单色消光系数\ \总有效横截面积,ns \,吸收和散射光子的波长的粒子,每个卷V在某个位置r n,在时间t的方向入射光子。如果光子穿越距离dl,灭绝的有效容积,或减少音量在光子的波长可以传播,dV \给出的
-
- 图3.5。体积体积灭绝的一个元素。光辉的分数AI \代表这些光子被散射传入的立体角,du,对原来的方向,n,或吸收的粒子。
因此,光辉,第九,这是一个测量单位面积上的光子,是减少后,迪克斯距离dl在根据dI \ dVx体积V
第九V
如果光子旅行距离L以上方程可以集成给兰伯特的指数衰减法对光子第九= IoX tx (3.31)
IoX传入的光辉,tX的透射系数tX = e ~ TA (3.32)
定义的光学深度和tx rx = f xx (l) dl, (3.33)
在微分形式。
因此,如果光子的波长导线距离L然后的概率不是从最初的方向是由tx。因此,1 / xx代表一个特征长度,或长度恒定的光子的波长沿着他们的道路,因此衡量光子的平均自由路径遍历这个元素的体积。因此,光学深度是穿越光子的物理距离单位平均自由程。我们因此定义有效的光学表面的位置附近的大气光学深度统一(如太阳能光球层)。
对大气没有重大修改随机热运动的宏观运动吸收/散射粒子,x是各向同性。它有两个组件,一个吸收组件,k和散射分量,x \ (r, t) = Kx (r, t) + ax (r, t) (3.35)
因此,光子散射事件发生的概率而不是吸收事件称为单散射反照率,w,由用户体验(? t) = ax (r, t) / xx (? t)。(3.36)
3.4.4卷发射和基尔霍夫定律
量排放,r / X是定义在波长发出的能量,方向n,单位体积每球面度每秒每单位波长,这样一个元素所发射的能量体积dE = nX (r n t)爸爸/ d ^ dAdt。(3.37)
黑体,这也可以写的排放系数,e代表有效发射表面单位体积dE = (r, t) BX交货(r n t)爸爸/ d ^ dAdt。(3.38)
在没有散射的情况下,被一个元素吸收的能量可以编写体积相当于dE = KX (r, t)第九(r n t)爸爸/ d ^ dAdt。(3.39)
如果元素的体积是一个封闭的系统内热力学平衡(TE),然后第九= BX和光辉由普朗克函数,给出一个黑体的辐射。在TE过程都在平衡等辐射平衡(重新),所以通过体积元素散发和吸收的能量是相等的nX (r, n, t) = KX (r, t) lX (r, n, t)。(3.40)
因此,黑体,发射系数是相同的吸收系数(r, t) = KX交货(r, t)。(3.41)
这就是所谓的基尔霍夫定律。体积存在黑体发射的总量排放可以写成一个热的总和和散射分量r / X (r n t) = KX (r, t) BX (r, t) + nXscat (r, n, t)。(3.42)
热组件是各向同性,而散射分量一般是各向异性的。
3.4.5源函数和再分配
总体积的比值排放总量灭绝叫做源函数
在没有散射的情况下,我们只有热发射和源函数等于普朗克函数。因此,对于热辐射Sx = Bx。更一般地,我们可以把源函数写成两个组成部分的总和的单散射反照率
Sx (r, n, t) =(1 -天气(r, t)) Bx (r, t) + wx (r, t) Sx8cat (r, n, t)。(3.44)
散射源函数通常是各向异性的,取决于传入的辐射和散射机制或photon-redistribution流程。光子能量再分配和方向可能发生结果的束缚束缚测试过程或散射光子的粒子。这个过程是所描述的再分配功能,R,使光子能量的再分配联合概率密度和方向。因此有意义的讨论光子再分配的光子频率,v,而不是光子的波长。因此,联合概率方向入射光子的n和v被吸收并重新发出的频率或分散方向n v是频率
v y 4 n 4 n和归一化条件
首席运营官粪便
这严格适用如果散射粒子不接受非弹性碰撞与其他粒子的大气,吸收和发射之间的时间。
散射体积排放的再分配函数可以写成
- J - J dv R (v、n;z / n) Iv”(r n t)。(3.46)
3.4.6限制形式的再分配功能
一般再分配功能非常复杂,但有两个限制使用简单的形式,根据其物理应用。大气分子(瑞利散射)、气溶胶和云滴(米氏散射),频率分配并不重要,只有光子重定向。对谱线测试,因束缚束缚过渡,情况正好相反。粒子散射因此被认为是在频率和相干散射系数,合资企业可能是一个复杂的频率的函数,根据不同的大小和颗粒的物理化学性质。测试束缚束缚电子散射过程的转换通常是被各向同性只有频率分配考虑。
3.4.6.1各向同性散射在静态的气氛中,我们可以平均分配函数对所有传入或传出光子方向获得direction-averaged频率再分配功能
4 n 1
平均只需要执行的方向在入射光子的方向或即将离任的光子的方向,为再分配函数只取决于角e,光子之间的传入和传出的方向由n×n = cos e (3.49)
归一化条件foo
氛围的重要宏观运动获得direction-averaged必须小心再分配功能,由于多普勒效应变得重要和需要平均参考系的粒子和观察者的。这是因为在观察者的框架,多普勒效应是强烈依赖的方向,导致高度各向异性散射。
对于各向同性散射,e的再分配功能是独立的,所以它也可以写R (v, v)和体积的散射分量排放可以表示的意思是光辉企业>,由eqn定义(3.8),p O
nvscat (r, t) = av (r, t) r (v, v)合资> (r, t) dv。(3.51)
我们可以平均分配函数,R (v, v),对所有即将离任的光子频率,v,获得吸收概要或概率密度吸收一个光子的频率v, ^ > (v)从y (v) = / R (v, v) dv, (3.52)
与归一化条件
排放,^ (v),或概率密度发射的光子频率v,被定义为
乔(r, t) dv乔< fi (v)合资(r, t)的dv
这个表达式认为如果弹性散射散射粒子的速度(没有变化)和其他没有耦合约束状态,这是我们认为只有两个电子能级之间的转换。
因此,一般的吸收和发射配置文件是不一样的。在特殊情况下,他们都是相同的。从上面的方程我们可以看到,如果平均辐射很弱不同频率和再分配功能的函数是对称的(v, v) = R (v, v),然后^ (v) = y (v)。另一个案例中出现碰撞时吸收粒子和所有其他粒子非常频繁(高压),这样我们有完整的再分配的频率。这种情况将进一步讨论后,我们考虑谱线展宽机制。
3.4.6.2相干散射频率分配是不重要的时候,我们可以单独再分配为光子重定向一个概率密度函数,描述了一个相位函数,p,和概率密度相干散射的频率。束缚束缚电子转换再分配功能的形式
R (v、n;v、n) = p (n, n) y (v) 5 (v - v), (3.55)
5 (v - v)是狄拉克δ函数,而对于粒子散射,如瑞利和米氏,它的形式吗
和相位函数是一个函数的cos e和规范化根据j) p(聊天)dQ = 1。(3.57)
对于各向同性散射p(因为e) = 1,我们可以定义一个不对称因素,g,量化的扩展non-isotropy我r1的散射过程
不对称因素有以下值根据g = 1向前散射散射过程
= 0各向同性或对称散射
= 1向后散射。
为了方便起见,如果我们为各向同性散射j = cos然后p (j) = 1,或对称散射(瑞利)p {jj) = f (1 + p2),不对称因素是零。米氏散射或由大粒子散射,定义的参数x = 2 nr / > 1, r是粒子的半径,典型值接近0.8的不对称因素。等水滴散射代表本质上向前散射由于折射。这种散射相位函数是复杂的,然而,有近似函数表达式如Henyey-Greenstein阶段
mGip) = (1 + 2 ^ ^) 1 - (3 ' 59)
上面的相函数给出了一个好的近似向前散射峰,米氏相位函数近似,这水滴有很强的前锋峰由于折射和疲软的向后峰由于内部反射,是由p (j) = phg (j;gi) + (1 - b)越南河粉(j。92)。(3.60)
例如,上述方程使海洋气溶胶散射的真实值= 0.7 jm, g1的值= 0.824,g2 = -0.55和b = 0.9724。
3.4.7源函数的形式
3.4.7.1各向同性与各向同性和束缚束缚电子的相干散射转换方向和频率相干散射,散射volumeemission组件是由nvscat = Vv 4 > (v) 5 (v - v)合资企业,dv, (3.61)
和总量排放的形式nv = Kv Bv + Vv w (v)合资企业,(3.62)
而源函数写成
其中紫外线是单散射反照率。粒子散射的总量排放的形式nv = Kv Bv + Vv合资企业,(3.64)
和源函数
继续阅读:F vnAAOs
这篇文章有用吗?




