方法1趋势不确定性方程的细节
下面的步骤展示了如何使用A类和B类敏感性计算趋势不确定性(参见3.2.3.1节)。
1)评估Y年水平不确定度的方法假设类别和气体是不相关的,或者假设类别和气体是聚合的,直到聚合的类别可以被视为不相关。
2)该国总排放量(M列脚下的量)趋势的不确定性估计为:
其中UT是该国总排放量趋势的不确定性,U是由类别和气体引入UT的不确定性。
3)我们采取
Ui,其中UEi是第i类气体排放因子相关的不确定性引入Ui的不确定性,UAi是第i类气体活动数据相关的不确定性引入U的不确定性。
4)从E列和F列中,我们知道与i类和气体的活动数据和排放因子相关的不确定性以百分比表示,但我们还不知道这些不确定性如何影响总排放量的趋势,这是我们对UEi和UAi所需要的。为此,我们写下
其中Ai是与i类和气体相关的A类敏感性,uei是与F列中的排放因子相关的百分比不确定性,Bt是与i类和气体相关的B类敏感性,uai是与e列中的活动数据相关的百分比不确定性。基本上,A类和B类敏感性分别是与基准年和Y年之间自相关的百分比差异相关的弹性。另一个与总排放量的百分比变化无关。该方法允许反转这一假设,或者排放因子和活动数据在年份之间都是自相关的,或者两者都不是自相关的。
5) A类和B类敏感性可从基准年和Y年类别和气体总和的趋势公式中计算。引入附加因子V2是因为不相关的不确定性可能影响基准年或Y年。目前的公式假设B类敏感性Y年的排放量与基准年的排放量没有太大差异;如果情况并非如此,我们将不得不对不相关的不确定性分别引入基准年和Y年的考虑,而不是使用V2因子。
a型灵敏度的推导
趋势可以写成(假设1990年为基准年):
f N N
2ei,y - 2ei,1990 i=1_i=1_
如果i类和气体在整个过程中增加了1%(与A类灵敏度捕捉到年份之间相关的不确定性影响的假设一致),趋势将变为:
2ei,y + 001 ei,y - i2ei,1990 + 001 ei,1990
灵敏度Ai为:
2 ei, y + 001 ei, y -I 2 ei,1990 + 001 ei,1990
2 ei,1990 + 0-01 ei,1990 i=1
f N N
2ei,y - 2ei,1990
这与GPG2000第6.18页注B中给出的A型灵敏度的表达式相同。b型灵敏度
B型敏感性我们假设i类和气体每年仅增加1%。在这种情况下,趋势变成:
eei,y + 001 ei,y - eer,1990
所以灵敏度Bt变成:
y 1990
ei,y - ei,1990 i=l_i=l_
分子上的所有项都消掉了除了0.01乘以100就变成了。因此,GPG2000第6.16页中B,-的表达式化简为y列J。
N就是上面的表达式
3.7.3处理方法1结果中较大的不对称不确定性
本节提供了关于如何纠正方法1中不确定性大估计的偏差,以及如何将不确定性范围转换为基于对数正态分布的非对称95%概率范围的指导。
对大不确定性的不确定性估计的修正:方法1的近似误差传播方法产生了对不确定性半范围(U)的估计,以相对于库存结果平均值的百分比表示。当存货总不确定性中的不确定性变大时,误差传播方法系统地低估了不确定性,除非模型是纯加性的。但是,大多数清单是根据各项的总和估计的,每一项都是一个产品(例如,排放因素和活动数据)。误差传播方法对于这样的乘法项是不精确的。实证研究结果表明,在某些情况下,使用方法1估计的不确定性可能被低估;分析师可以使用修正因子,例如Frey(2003)提出的修正因子。Frey(2003)评估了一种分析方法的性能,该方法将不确定性与大样本量的蒙特卡罗模拟相比较,用于涉及加性、乘性和商模型的不同不确定性范围的许多情况。误差传播和蒙特卡罗模拟了模型输出的不确定性半范围的估计,对于小于100%的值很好地一致。当总库存的不确定性增加到较高水平时,误差传播方法对总库存的不确定性有系统的低估。模拟结果与误差传播估计之间的关系被发现表现良好。 Thus, a correction factor was developed from the comparison that is applicable if U for the total inventory uncertainty is large (e.g., greater than 100 percent) and is given by:
不确定度半程修正因子
注意:如果U > 100%,且模型包含乘法或商项,则使用。对于U >不一定可靠。230%对于纯相加的模型没有必要。
地点:
U = /-误差传播估计的不确定性范围,以百分比为单位
Fc =方差分析估计的校正因子,校正不确定度与未校正不确定度的无因次比
当U从100%到230%变化时,基于经验的修正因子产生的值从1.06到1.69。修正因子用于开发一个新的,修正的,对总库存不确定性半范围的估计,ucorrecated,反过来用于开发置信区间。
修正后的不确定度半程
地点:
Ucorrected =修正后的'/2-误差传播估计的不确定度范围,单位为%
在不确定度半范围(U)小于大约100%的情况下,方差分析估计中的误差通常很小。如果对U在230%以下的值应用修正系数为U > 100%,预计在大多数情况下U估计的典型误差在正负10%以内。校正因子对于较大的不确定性不一定可靠,因为它的校准范围为10%至230%。
计算大不确定性的非对称置信区间:为了仅基于不确定性的均值和半范围计算模型输出的置信区间,必须假设分布。对于纯粹是可加性的模型,并且不确定性的一半范围小于大约50%,正态分布通常是模型输出形式的准确假设。在这种情况下,可以假设一个关于平均值的对称不确定范围。对于乘法模型,或者当一个变量的不确定性很大且必须为非负时,对数正态分布通常是模型输出形式的准确假设。在这种情况下,不确定性范围相对于平均值不是对称的,即使从方法1可以正确估计总库存的方差。在这里,我们提供了一种基于误差传播结果计算近似不对称不确定性范围的实用方法,该方法基于Frey(2003)开发的方法。95%置信区间的一个关键特征是,它们在小范围的不确定性中近似对称,在大范围的不确定性中正倾斜。对于非负变量,后一个结果是必要的。
对数正态分布的参数可以用几种方式来定义,比如用几何平均值和几何标准差来定义。几何平均值可以根据算术平均值和算术标准差来估计:

地点:
|g =几何平均值I =算术平均值几何标准差由:

地点:
CTg =几何标准差
置信区间可以根据几何均值、几何标准差和标准正态分布的累积概率逆分布(带有对数变换)来估计:
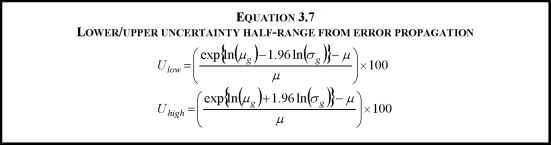
地点:
Uiow =误差传播估计的不确定性的下^-范围,以%为单位。
Uhigh =误差传播估计的不确定度的上Grange,单位为%。
为了说明这些方程的用法,考虑一个例子。假设平均值为1.0,误差传播估计的不确定性Grange为100%。在本例中,几何平均值为0.89,几何标准差为1.60。95%的概率范围作为相对于平均值的百分比,由公式3.7中从Uiow到Uhigh的区间给出。在本例中,结果为-65%到+126%。相反,如果使用正态分布作为不确定度估计的基础,则估计范围约为±100%,获得负值的概率约为2%。图3.9说明了95%概率范围的下限和上限的灵敏度,分别为2.5个和97.5个百分位,假设基于误差传播方法估计的不确定性半范围的对数正态分布。不确定度范围相对于平均值近似对称,不确定度的一半范围约为10%至20%。随着不确定性半范围U变大,图3.9所示的95%不确定性范围变大且不对称。例如,如果U是73%,那么估计的概率范围大约是-50%到+100%,或者是两个因子。
图3.9相对于算术平均值的非对称不确定性范围的估计,假设基于误差传播方法计算的不确定性半范围为对数正态分布
图3.9相对于算术平均值的非对称不确定性范围的估计,假设基于误差传播方法计算的不确定性半范围为对数正态分布

100 150
不确定度半程(%)
100 150
不确定度半程(%)
继续阅读:确定关键类别的方法方法
这篇文章有用吗?