冻融地面的热物理过程

1.1地面传热与温度场

的温度制度岩石圈上部的热作用是与环境(大气、空间等)以及与下面地层相互作用的结果。从大气(主要来自太阳)到达地球的热量大约比从内部到达地球的热量大3个数量级。的传热过程在地面上一般通过辐射、对流和传导进行。

热辐射代表了辐射的过程电磁波(辐射能)由受热的物体释放到环境中。绝对黑体发射的最高值所对应的波长与其绝对温度成反比。那部分热转移地面内的辐射通常只占总热通量值的百分之几。

对流换热(qcon)是液体和气体在岩石中的孔隙、孔洞和裂缝中流动所进行的传热，土壤中水分迁移(扩散)过程中所传递的热量通常比传导传递的热量要小。在断裂的坚硬或粗糙的碎屑岩和砂中，强迫水和气对流(渗透)的情况传热机理在温度场分析中起着重要的作用，忽视这一机制可能会造成根本性的误差。通过有效导热系数Xe(涵盖包括对流和传导在内的总传热，或通过直接计算热通量密度q，例如与水或孔隙溶液的渗透有关:qcon = yw/ filvw，其中yw为水的密度；Vw为其过滤速率，/fil为渗透水(溶液)的比相对热含量。

地面传热的主要和最基本的机制是传导。热是通过介质中原子和分子振动的结果晶格，其强度随温度的升高而增大。这发生热传递由于材料的导热性。从数学的角度分析了静止导电的过程传热是用傅里叶定律表示:Qcood = grad t，其中Qcood为热通量导电分量的密度;X为介质的热传导系数，在数值上等于单位时间内在单位温度梯度下通过单位面积的热量。

表征岩石热状态的主要参数是温度。它在地面上的分布称为温度场。一般来说，地面温度从一点到另一点随时间变化，即温度场由三维非平稳函数t (x, y, z, t)描述。在自然界中，温度场通常在两个甚至其中一个空间坐标中变化显著，而在另一个空间坐标中几乎不变。为了与此保持一致，通常使用术语“二维f(x, y, t)”或“一维t (x,t)”温度场。温度场以图形方式显示为连接相等温度值的等温线(线或面)(图1)。1).如果温度场在任何一点上不随时间变化，则称为平稳场(见图1.1 a);反之为非平稳(见图1.1b)。采用傅里叶热传导方程和适当的边界(初始)条件对非平稳传导传热过程进行了数学描述，并计算了温度在时间和空间上的分布。在一维温度场的情况下，它的形式为:

式中/(z)为分布热源或热源的强度;Cvol (z)是的系数热容量介质的热量，其数值等于将单位体积的物质加热1°C所需的热能。在最简单的情况下，当介质具有恒定的热物理特性且没有热源时(A = const, Cvol = const，/(z) = 0)，非平稳热传导方程为:

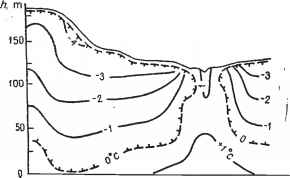
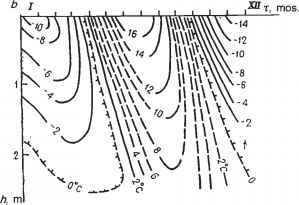
图1.1。温度场的图形表示实例:a -二维平稳;B -一维非平稳。0°C等温线是未冻地和冻土之间的边界。

where a = a /Cvol the热扩散率索引的:作为…索引的热惰性媒介的。

在非平稳的热状态下，温度场在时间上的变化可以相当多变(从单调到痉挛)。周期性稳态场是自然条件下非平稳温度场的重要代表。它们的特点是介质中初始温度分布的影响几乎随着表面温度的反复波动而消失。这种分布可以说是“从介质的记忆中抹去”，可以从某个时刻开始忽略。正是这个瞬间指出了这个过程的周期性稳定状态。

周期静止状态的最简单同时在自然界中最普遍的情况是每天、每年和常年空气温度波动的正弦波，以及由它们引起的地面温度的同一正弦波(谐波)波动。在这种情况下，我们可以说温度波通过地面的传播。我们可以用简单的关系式来表示这些温度变化:

n 2。TC

式中f(0, q)为地表温度随时间的变化;A0是该温度在年(或日或年)周期中波动的物理振幅(等于气象温度的一半);ean是地表年平均(日平均或多年平均)温度，以其为中心进行周期T的波动。因此，表面的温度波动由三个值决定:ean, A0和T。

很明显，在自然条件下的实际温度，例如地表的年温度模式，与正弦曲线有本质上的不同，因为在全年的温度变化的一般背景上存在不规则的增温和降温(图1.2a)。但是，如果在10天期间，特别是在几个月期间平均温度，温度曲线将越来越接近正弦形式。在一般情况下，通过实验确定位于零温度轴和T等于一年的实际温度变化曲线之间的面积和S2，这条曲线总是可以变成“理想的”(完美的)正弦形式。这种“理想”正弦波的主要参数，即年平均地表温度f°ean和温度波动的物理振幅A0，在这种情况下可以通过以下方法计算:

o _ Si ~ S2 ^ St + S2 n

地表的温度波动f(0,x)引起地表的温度波动t(z,q)，即地表形成的温度波传播到地面激发了地面的相似的温度波。与此同时，当波向下移动时，会遇到热阻(该值与热导率值X成反比)，并在与介质的热容Cvol相关的过程中消耗其能量。因此，波随深度而衰减，A0逐渐减小。最大穿透深度为vt°c

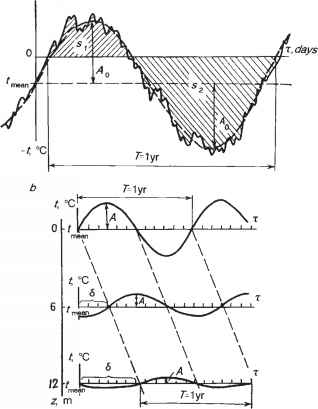
图1.2。地表和地下的谐波温度波动:a——地表观测到的温度降至“理想”正弦波动;b -地温波传播:A -波动幅度;<5-波动St和S2的时移-温度，度小时，分别在暖期和冷期。

图1.2。地表和地下的谐波温度波动:a——地表观测到的温度降至“理想”正弦波动;b -地温波传播:A -波动幅度;<5-波动St和S2的时移-温度，度小时，分别在暖期和冷期。

地表温度波(常年、年、日)的地面称为温度波动的传播深度或零(常年、年、日)温度振幅的深度。用这些深度值划分的近地表分别称为常年(n年)、年或日温度波动层。

温度波在无相变介质中的传播可以用傅立叶定律来描述，该定律是由求解温度波在无相变的无界半空间的均匀介质中传播的所谓傅立叶问题得来的。该问题的数学公式如下:

的意思是

在这个问题的公式中没有初始条件，因为它假定传热过程已经处于稳定的周期状态。该问题的解决方法如下函数:

该函数确定了在相应的地表温度变化下，任意深度z和任意时刻x的地温值。它完整地描述了地表正弦波温度波动在地表形成的稳态周期性温度场。在此解的基础上，我们可以得出在地面上也建立了与地表相同的平均温度i°ean和周期T附近的波动(见图1.2b)。对所给出的解的更复杂的处理使我们能够陈述以下被称为傅立叶定律的关系，这些关系是温度波传播到地面的过程的基础。

傅里叶第一定律指出，温度波动的振幅随深度呈指数下降:

从这个关系可以得出，温度波动的衰减速率随深度的变化取决于介质的性质:热传导越高(热阻越低)，热容越低，衰减速度越慢，温度波动渗透的深度就越大(其他条件都相同)。

每一特定深度正弦波温度波动最大值和最小值的曲线为指数曲线，定义了温度波动幅度随深度衰减的特征(图1.3)。换句话说，温度波在均匀介质中传播的傅里叶问题的解表明，所有可能的温度随

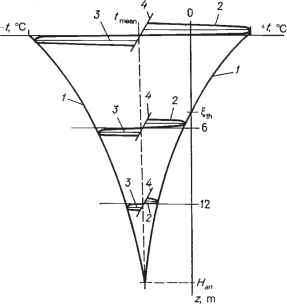
图1.3。温度波动随深度衰减的性质。1 -温度波动包络线;2 -表面和6米和12米深处的温度波动;3-4 -深度0、6和12 m的波动幅度和时间轴;MTH为季节性地面融化深度;H.为年温度传播深度。

图1.3。温度波动随深度衰减的性质。1 -温度波动包络线;2 -表面和6米和12米深处的温度波动;3-4 -深度0、6和12 m的波动幅度和时间轴;MTH为季节性地面融化深度;H.为年温度传播深度。

深度被限制在每个特定深度的特定边界内。这些边界是指数曲线r°ean + A(z)的段，其中z在0到0年振幅深度的范围内变化。因此，如果将全年洞内温度测量的实际数据输入到一个图中(图1.4)，同步温度曲线可以说将“填满”指数曲线段所包围的区域。为了显示温度随深度的变化，地质学家通常使用这些信封，而不提供特定时间瞬间的特定温度曲线(见图1.3)。

傅里叶第二定律指出地面温度的波动是以a为过程的相移与深度成正比(见图1.2 b)。涨落延迟的时间可由下式计算:

波动随深度的相移是由于

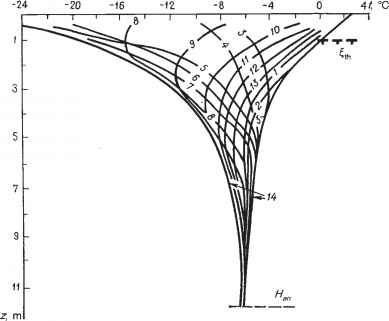
图1.4。雷竞技csgo14 -信封的曲线。另见图1.3。

图1.4。雷竞技csgo14 -信封的曲线。另见图1.3。

波通过地面传播速度的限制。这velocity depends on the thermal-physical properties of the ground and on the period of the fluctuations; therefore it is constant with depth and with time for homogeneous ground. In line with this law of Fourier, the minimal winter temperatures at some depth z, for example, will be observed not at the moment of their occurrence on the surface but after the time necessary for the wave to reach this depth z. Therefore under natural conditions the following pattern is observed: when, for example, a period of cooling or warming begins in the near-surface portion of the ground the period of warming (or cooling, respectively) is still in progress in the middle part of the layer of the annual temperature fluctuation, while the period of cooling (or warming) of the previous temperature wave is observed in the lower portion of the layer (see Fig. 1.4, curves 8 and 10).

傅里叶第三定律将温度波动的穿透深度h与温度波在表面的周期和振幅联系起来:

从这个关系出发，可以证明波动渗透的深度随着振幅A0和波动周期t的增大而增大。温度波动(阻尼)渗透的最大深度被认为是振幅Ah小于0.1°C的深度，即相当于自然条件下温度测量的精度。将Ah = 0.1°C和波动周期T的各种数值代入式(1.8)可以看出，在其他条件相同的情况下，周期较大的波动穿透深度最大，而周期短的波动在地表附近被阻尼。实际上，通过计算和自然观测，气温的日波动深度可达1-2 m，年波动深度可达15-25 m, 300年波动深度可达150-200 m及以下。根据傅里叶第三定律，给定两个周期不等的波动7\和T2(7\¥iT2)，波动发生相同阻尼的深度zx和z2之间存在以下关系:

因此，给定1年和100年两次地表温度波动，如果已知年振幅减小10倍在10米深处，由式(1.9)可以得出，在100米深处，100年波动的幅度也会出现类似的衰减(衰减10倍)。

总的来说，由于近地表地表存在周期性(谐波)温度波动(温度波)，将地表温度变化的年(日或常年)周期分为升温半期和降温半期。在加热的一半时间里到达地面的热量和在冷却的一半时间里从地面流出的热量通常被称为地面热周转量geocryology．在稳定的周期性温度状态下，每个半周期的热周转量大小相等，但符号相反。正如Y.A. Kudryavtsev(17)所示，当热量通过无相变的干燥均质土壤传播时，z层地表热量周转量的表达式为:

需要强调的是，上述关于地面温度场形成的所有原理都没有考虑到水分相变的影响以及水平和某些垂直热通量的存在。因此，例如，当考虑地热通量q的存在时，年温度波动层深度内的地表年平均温度imean不是恒定的，而是随着地温梯度g而增加，即:

地温梯度(g = q/X)表明，对于给定的位置，随着单位长度的深度变化，温度变化了多少度。地温梯度的倒数称为地热深度。它显示了沿垂直方向地面温度变化1°C的距离。在进行近似计算时，通常认为各大陆的地热深度平均为33米。

除了来自地球内部的垂直热通量和岩石圈上部相关的地热温度梯度外，还有横向热通量，因此也有横向温度梯度。在相对于太阳方向不同的地形元素与另一地形元素之间、坡度和含水量高低之间、陆地与海洋和湖泊盆地之间以及大型水道之间的边界处，岩石中观察到极高的水平温度梯度。换句话说，自然界中常常存在二维和三维的温度场，而不是一维的。

当潮湿土壤和地面系统的温度超过0°C时，温度场的形成原理要复杂得多。这与过程有关水冻结或冰融化(水相变)伴随着大量热量的释放或吸收，从根本上改变了温度模式。就其性质而言，在这种情况下，它不仅仅是一个冷却或加热地面的过程，而是一个更为复杂的过程冷冻过程或者是潮湿地面的融化。人们应该考虑潮湿土壤系统中水分相变的本质，以正确理解和分析这一过程。

1.2水的冻结(结晶)和地下冰的融化

当温度超过0℃时，潮湿土壤的组成、结构、性质及其组分和相之间的相互作用极其复杂。所有的天然水都是有效的溶液，即由不同程度上被溶质离子束缚的水分子组成。在土壤中，离子与水的结合也伴随着与矿物颗粒(吸附水)活性表面的相互作用。因此，在研究土壤中束缚水的结构和相变时，有必要将自由体水结构模型作为主要的比较标准。

和a。a。anyanan, b。n。dostovalov, o。ya。Samoylov,丫。一、Frenkel等研究人员对无冰水蒸气相变过程(冰的分解过程)的发展可以用以下方式表示(11)。当冰的温度接近0℃时，位于冰晶格点上的每个分子具有最小的动能EK和最大的活化能，即结合键能EB或与周围分子的相互作用能。在这种情况下，EK值被证明大大小于EB值。分子运动的速度随着向冰的热输入而增加。

入射的能量可以用来克服冰结构中特定分子之间的键，并使分子在EK > EB时执行平动跳跃。随着能量作用的继续，会有超过9-13%的氢键断裂，等温熔化过程开始。氢键断裂的比例由熔解热(5.9 kJmol ~ *)和升华热(48.1 kJmol”1)的关系确定。

H20分子中如此多氢键的断裂是由于分子平动跃迁数量的增加导致冰晶点阵中形成了足够数量的空位。因此，对称和窗状的长期秩序的冰结构打破了，它是碎片。与此同时，不再像在冰中那样有秩序地相互连接的分子群或结合体在晶体体中分离或孤立。形成这种分离的缔合物需要满足两个条件:1)在相邻分子之间和沿水缔合物等高线的若干氢键必须断裂;2)使分离的分子群(“冰块”)围绕它们的平衡中心产生振动(布朗运动)。后者的发生是由于H20分子的脉冲传输。在这种情况下，分子在晶格点上H20旋转振动运动的能量增加几乎停止。与此相关，没有进一步增加冰的温度随着热浪的持续到来。

在冰的融化过程中，最大和最慢的H20分子组合在单个平移分子及其群的动量的作用下可以被分解并分裂成较小的分子。在这种情况下，冰和水的总体积减少了，而密度却增加了，这是由于六边形冰结构中的一些四面体被打破，它们的分子渗透到仍然存在于晶格未破碎部分的空隙中。这样的体系中分子的配位数增加到4以上，即每个分子的氢键数增加，即活化能增加。换句话说，在平均达到某种临界质量后，缔合的进一步断裂就停止了，而到达的热量主要用来增加缔合分子和缔合本身的动能。系统的温度开始上升，同时熔化和氢键的进一步断裂停止。

根据以上所述，可以很容易地考虑这个过程的相反过程，即水变成冰的过程水的过程冻结)。因此，平移跳跃的数量和扩散的H20分子的速度以及小的水结合的速度随着从水中提取热量而降低。平移粒子传递的力矩减弱了。在平衡中心周围，构成水结构骨架的大分子组合的振动会减慢。水温下降是自然结果。分子间的氢键越来越迟钝，这意味着H20分子之间的氢键能够将分子的基团和基团保持在一起。分子的布朗运动变慢，然后完全停止。缔合体增大、统一和平均质量增加到临界点以上，即缔合体发生转变，形成冰晶核，冰晶核迅速生长并释放结晶热。较小的关联以及孤立的扩散的H20分子开始加入这些扩大的分子。由于H20分子在冰晶格中的配位数小于水晶格中的配位数，等于4，并且由于冰结晶为具有自由通道(空穴)的六方晶体体系，因此随着水向冰的转变，体系的体积增大，而密度减小。 An expansion of water by 9% occurs on its transition into ice.

上面讨论的H20基团和分子的统一和扩大过程伴随着H20分子之间必要的新氢键的形成，自然伴随着必须从系统中释放的热量。

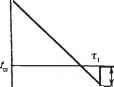
可以认为，冻结过程是突然进行的。对于a b

上餐

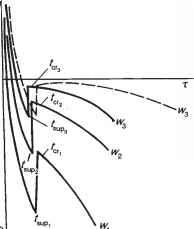
图1.5。(a)水和(b)冻结粘土在不同初始含水量Wl < W2 < W3和恒定热去除率的情况下，过冷和结晶过程中温度随时间(t)的变化，Q'(实线)和Q2(虚线)，Q'^Qy为例，当(a)水和(b)冻结粘土过冷和结晶过程中温度随时间的变化冰的温度冰晶减少，系统中的温度开始平衡，与冰晶接触的水的温度必须降低。然而，在这种情况下，水不能降低其温度，因为它会转化为冰(即H20分子的结合可以发生)。换句话说，任何局部冰晶温度的降低或H20分子结合温度的降低都会导致部分水的结晶和转变为冰。因此，系统的温度不能降低，直到所有的水转变为冰发生(图1.5a)。这就是为什么冻结过程是等温的原因。伴随缔合的剧烈增大，以布朗运动和结晶热的释放为特征。然而，我们可以假设，在某些情况下，由于从冻结系统中快速散热，冻结过程基本上是瞬间进行的。在这种情况下，结晶热不会释放，因为水的纹理不会转变为冰的纹理。因此，H20的结构是“固定的”，形成了所谓的无定形(非结晶)冰结构。

水结晶理论中最复杂和最不明确的问题之一是建立水分子成为冰晶核时的临界质量问题，即就其结构而言，它们转变为完整的微晶体。近年来的研究允许假设这发生在临界质量为472 h2o的情况下。这个单位冰电池的大小被认为是10英寸20立方厘米左右。当达到这样的质量时，这些结合可以密集生长，并成为未来晶体的基础。晶体通常从核的中心呈放射状生长。从热力学的角度来看，附加的力将H20分子和缔合物结合到冰的结构中，即形成一个或多个结晶中心，是开始结晶过程所必需的。

关于冰微晶发育的性质有两种理论。其中一种(均相)认为结晶中心的形成是一个规律的过程，介质中均匀的温度下降导致分子间的缔合形成足够质量的H20分子，使分子运动速度减慢，分子通过氢键结合在一起。冰晶形成的非均质理论是基于熔体(水)中不可避免地存在作为天然种子晶体的外来颗粒(杂质)，即作为结晶中心。非均质理论并不排除晶体均质起始的理论可能性。然而，由于实际上不可能将水从杂质中分离出来，实际上正是这些外来颗粒导致了水的结晶。

当液体过冷到低于冰点的温度时，过渡到亚稳态是均匀冰晶形成的必要条件。这种单位晶体是自发形成的，它的未来取决于溶液的过冷程度。在足够的过冷条件下，晶体会生长。计算表明，在0 ~ - 55℃的温度范围内，水可以处于亚稳态。超级酷是可能的蒸馏水到- 12到- 16°C和小水滴到- 72°C的实验。在这样的温度下，整个液滴体积立即开始结晶。水体积的过冷通常不超过几度，取决于水的成分、形成的背景和冷却速度。

根据非均质理论，在熔体过饱和或过冷的情况下，强迫结晶是由种子晶体引起的。最好的种子晶体是生长晶体(冰)本身的颗粒(杂质)。其次是能与晶体形成固溶体的同构物质的颗粒，即所谓的天然气水合物和结晶水合物。这种杂质的原子或离子占据了水晶体晶格的角落。不溶于水的盐晶体、各种机械不规则以及在一定条件下与生长晶体有规则聚集的物质也可作为种子晶体。总的来说，所有具有类似于冰的结构的固体都必然引起结晶。

冰晶的进一步生长(在核形成之后)一方面取决于晶体化学结构的特殊特征，另一方面取决于它的吸收条件。因此，在温度梯度不变的情况下，晶面不断增大，水转变成冰所消耗的能量不断增加，晶体周围的水温在开始时会略有上升，从而使晶体的生长速度变慢。随后，随着温度的降低而移到系统外释放热量在水的过程中开始结晶。换句话说，冰晶在水中的生长很可能是间歇性的和周期性的。随着生长晶体周围的水的轻微加热和进一步冷却，这种差异水的密度能够引起温度扩散以及H20分子的扩散，从而导致质量流入晶体的各个部分，导致其生长。晶体边缘和顶点(角)周围的生长速度比晶面附近的生长速度要快，即观察到生长的各向异性。冰针和星之所以形成，是因为晶体顶点伸长得更快。后来，它们一起生长成一个连续的团块，仅沿边缘保持骨架形状(19)。在单侧均匀冷却的条件下，这将导致朝着最有利方向的晶体的选择和初级生长。朝向不利方向的晶体被楔出。与此同时，如果一个正在生长的晶体面遇到任何异物，它就会开始用一种被称为结晶力的力把这个异物推开。

在含有溶解盐的天然水中，结晶过程中经常观察到组分的分化(分离)。在冷却这种溶液的过程中，盐分子和水分子被组织成基本晶格。冰的晶格和每种盐的晶格分别形成。这种分层是由冰晶格和盐晶格晶体参数的区别决定的。在冻结过程中，盐的基本晶格被排斥到冰晶核作用的力场边界。冰晶通常含有非常少量的盐，这是由冰格形成的条件决定的。同时，结晶速率越大，晶体捕获的盐量也越大。盐溶液的冻结(结晶)温度低于0℃。

水的能量储存为636吉克1，而冰的能量储存为302吉克1在温度下0°C。它们能量储存的差异(334 Jg“1)代表聚变潜热冰。这种从外部提供的热量用于水晶格的形成，即用于冰中H20分子和水中H20分子之间平均统计距离的变化。

束缚水向冰的相变问题，以及首先解释土壤中水的冻结温度降低的影响，是比较复杂的。很明显，在最一般的分子动力学背景下，束缚水向冰的相变过程必须与自由(体)水的模式一致。然而，人们应该考虑到，被矿物表面束缚的水具有不同于自由水的纹理特征。人们可以预见，由典型的自由水的H20分子组成的骨架晶格在束缚水的纹理中是不存在的。结合水中的所有H20分子都有可能参与与矿物表面(底物)晶格的结构模式相对应的特定结构晶格的形成。这是由于外延机制将水结合到表面，随着固体衬底的靠近，结合水晶格的纹理模式与水合矿物晶体晶格的纹理越来越一致。同时，成键能逐渐增大。换句话说，矿物表面越接近，与自由水相比，束缚水的质地就越扭曲。因此，虽然构成水的结构骨架的大分子组合的振动应该基本减少，在温度下降的情况下，它们之间的氢键能够将它们结合在一起，这可能足以在自由水中形成第一个纯晶冰核，但这一条件并不足以在束缚水中形成第一个冰核。对于结合水，主要缺乏构成本体水结构格的大型H20缔合体，首先需要组织这种缔合体。 For this purpose sufficient lowering of temperature will be required to allow for a reduction of kinetic and vibrational energy of the individual molecules of bound water to an extent that the bond energy between molecules £b,or the activation energy, is greater than the sum of the kinetic energy and the bond energy between these molecules and the mineral substrate Em. In this case the hydrogen bonds of the H20

分子将能够克服矿物颗粒表面力的影响，并将分子组合成类似冰的组合。束缚水中形成第一个全晶冰核的条件为:

Eb>Ek + Em (1.12)

其中Em是一个变量值，随着矿物表面的靠近和结合水膜厚度h的减小呈指数增长，即Em =f[\/hn)，其中n是一个指数，其值取决于水与衬底之间相互作用的类型。将结合水的温度降低到tsup，等于满足这一条件所必需的过冷温度，将取决于水被矿物基质Em结合的能量值。水的结合水能量越大，它必须过冷的温度越低。因此，随着土壤初始含水量的降低(Wx < W2 < W3)，结合水膜厚度的减小以及H20分子与矿物表面结合能量的增加，过冷温度的负值逐渐减小(见图1.5b)。因此，束缚水在土壤冷却过程中的过冷，首先取决于从矿物颗粒表面力的作用中除去这部分水的必要性，而自由水的过冷仅仅是为了形成第一个全晶冰核所必需的。由此还可以得出，表面能取决于温度，即有效表面能的距离随温度而减小。

因此，一旦地面系统的温度达到与过冷束缚水的温度相等(tup < tj.”)，能量较少的束缚部分就不受地面粒子表面力的影响，从而形成单个H20分子的结合并使其增大。伴随缔合的布朗(振动)运动的停止(因为热量从体系中被移走)将导致它们转变为全晶冰核，以及单个H20分子和围绕这些或外来结晶核的小缔合的成组。与此同时，这一过程在束缚土壤水中进行不需要额外的过冷，因为，一方面，条件(1.12)的满足提供了必要的温度下降(到rsup < tj.”)，另一方面，孔隙溶液的特征是大量外来结晶核的存在，加速并加强了水分子重新组合成冰结构。随着相变热的释放，在土壤结合水中形成新的冰核并转化为具有完整质地的冰晶的过程自然发生。这将引起土壤系统温度的间歇性升高，从而使结合水上升到开始结冰或结晶的温度。”

土壤结合水结晶开始时的温度取决于土壤水分与矿物表面Em之间的键能值，实验研究表明，该键能越高，结合水膜越薄，结晶开始时的温度值越低。因此，沙子中水开始冻结的温度是由相当弱束缚(几乎自由)的水的高含量决定的，它接近于主体(纯水)的冻结温度(fj)。«0°C)。在这个温度下，所有的游离水都在沙子中冻结，冻结的时间取决于沙子的含水量和冷却的强度。如果从冻结的砂样中继续散热，其温度只会缓慢下降到大约- 0.5到- 1°C(图1.6)，这表明冻结出了越来越多的束缚水，这可以通过少量结晶热的释放来证实。富粘土中束缚水结晶开始的温度基本低于砂土，例如含水率为41-45%的蒙脱土可以达到- 2.5 ~ - 3.5℃的数值。在这种情况下，人们应该考虑到土壤结合水中溶质盐和交换阳离子的存在也会降低tJ的值。”从富粘土体系中进一步去除相变热导致负温度逐渐降低，因为越来越多能量束缚的水层被冻结(见图1.6)。因此，水分相变和结晶热的释放不是在一个特定的恒定温度下进行的，而是在一个负温度范围内进行的，在砂土(尽管不明显)和含粘土的土壤中。在这种情况下，只强调束缚水结晶开始的温度(r’c”)并不是不合理的。 The duration of crystallization of bound water as well as of free water will depend on the rate of heat removal from the system. A higher rate of heat removal will cause more rapid freezing out of bound water which is shown by a sharper knee in the curve of the freezing soil temperature change (see Fig. 1.5b).

为什么在第一个全晶冰核形成之后，温度必须在逐渐凝结的水层的连续冻结过程中下降

继续阅读:冻融土壤中的水转移和冰形成

这篇文章有用吗?

0 0