女朋友
0的0 h-1-i-1-i-1-i-1-i-1-i
频率f
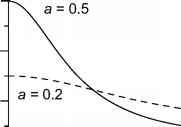
图5.1。AR(1)过程的谱(式5.13)。显示两个参数设置;d =1, fNy = 0.5。
5.1.2举例:AR(2)过程,离散时间
考虑离散时间AR(2)过程(第2.2节),参数a1和a2在等距时间尺度上,d > 0和n = to。然后(Priestley 1981:其中第4.10节),g(/) = 2d(1 + a2)(1 - a2)-1 [(1 - a2)2 - a2] [(1 + a2)2 (5.14) +a1 - 2a1(1 - a2) cos(2n/d) - 4a2 cos(2n/d)2]-1, 0 < / < 1/(2d)。AR(2)光谱图(图5.2)显示,除了红色之外,这些光谱还可能表现出准循环行为(Eq. 2.15)。
谱,g (f)
频率f
图5.2。AR(2)过程的谱(式5.14)。显示两个参数设置;d =1, fNy = 0.5。
5.1.3物理意义
功率谱密度函数h(f)和g(f)的重要性在于有可能将一个过程分解为来自不同频率区间的贡献。这样可以区分短期变化和长期变化,也可以区分气候系统的周期性强迫机制和宽带共振。raybet雷竞技最新这意味着光谱分析可以了解采样的气候系统的物理特性。raybet雷竞技最新与以往一样,当拥有的不是完美的知识,而是少量受测量和代理错误污染的数据时,任务是估计,即频谱。下面几节解释了从中推断h(f)或g(f)的方法
继续阅读:ExP[ie xout p a1 e .
这篇文章有用吗?