信息油水界面
h是时间滞后,E是期望算子和VAR是方差算子,给出了(其中普利斯特里1981:3.5节)
p (h) = | | h, h = 0±1,±2 (2.3)
> 0,这种行为可能会被称为“指数减少记忆”(图2.2)。
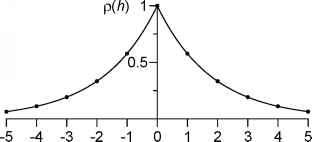
图2.2。AR(1)过程的自相关函数,a > 0。的情况甚至间距(2.1.1节)p h (h)是由一个| | = exp (- | | h•d / r),对于不均匀间距由exp(2.1.2节)(- | T (i + h) - T (i) | / r)。在这两种情况下,减少指数衰减常数t。
图2.2。AR(1)过程的自相关函数,a > 0。的情况甚至间距(2.1.1节)p h (h)是由一个| | = exp (- | | h•d / r),对于不均匀间距由exp(2.1.2节)(- | T (i + h) - T (i) | / r)。在这两种情况下,减少指数衰减常数t。
注意,假设在Eq。(1.2),即E Xnoise (i) = 0和VAR Xnoise (i) = 1,需要制定AR(1)模型的Eq。(2.1),这是不标准的。参见2.6节的标准制定。
持久性估计AR(1)模型参数的自相关估计,a。为了说明自相关估计,假设从时间序列数据,{x (i)}™= 1,去掉了异常值和趋势变化属性(Eq。1.2)确定和使用(图1.11)中提取{xnoise (i)}™= 1,实现噪声的过程。自相关参数的估计量,这意味着,一个食谱如何计算从{xnoise (i)}™= 1,给出
®- ^ ^ xnoise (i)•xnoise (1) / ^ ^ xnoise(我)。(2.4)
(第3章介绍了估计和“帽子符号”)。注意,估计是有偏见的,这意味着,如果{Xnoise (i)}是一个AR(1)过程参数,然后E(一)——一个。只有近似公式存在偏见的广义自相关估计。这些公式可用于偏差纠正。同样,也估计方差,VAR (a),只是大约。一般来说,偏差和方差减少n。背景材料(2.6节)提供了各种偏差和方差公式,通知其他偏差纠正和列表自相关估计。
适用性的AR(1)模型可以评估使用估计残差,
——xnoise•xnoise(我(我)
作为一个标准正态随机过程的实现,残差不应该表现出的模式lag-1散点图(图1.12)。
2.1.1.1有效数据大小
持久性(> 0)意味着减少信息内容的时间序列相比,情况没有积极的连续依赖性。在统计估计,更多的数据然后可用来实现相同的置信区间(第三章)宽度。一个有效的数据大小,n’,可以定义参数估计的过程通过估计方差与持久性。考虑均值估计量,X - X (i) / n,情商和AR(1)过程。2例(2.1):> 0 - 0。然后
(该指数是指平均估计)等于
贝利和Hammersley(1946)表明,n, n (n - 1)
可以为AR(1)过程的自相关情商。(2.3)使用几何级数迎刃而解以及算术几何系列:
1一个
冯·斯托奇和Zwiers(其中1999:17.1节)定义一个相关量,解相关时间
一个AR(1)过程从而td = (1 + 1) / (1 - a)。
即使是适度的n值(^ 50)和(^ 0.5),持久性的影响在n ^可以相当大(2.6节)。Eq。(2.7)只有均值估计量是有效的。因为n”的定义取决于类型的估计(冯·斯托奇和Zwiers 1999),这样的公式实用价值有限。2.6节给出了n '估计方差和相关性。
2.1.2间距不均匀
Eq。(1.2),我们让时间增加的不均匀间距d(我)> 0和编写离散高斯噪声AR(1)模型,
Xnoise (1) = EN (0, 1) (1)
Xnoise (i) = exp {- [T (i) - T (i - 1)] / T}■Xnoise (i - 1) (2.9)
+在(0,1-exp {2 [T (i) - T(张)]/ r})(我),我= 2,。,n。
“失去记忆”增加随着时间的时差了持久性,t(图2.2)。随机创新,E(■),现在的异方差的而不是同方差的间距。这是噪声模型不均匀间距为零的意思是,团结方差和自相关
E [Xnoise (i + h)■Xnoise (i)) = exp (- | T (i + h) - T(我)| / T)。(2.10)
使用噪声数据持久性的时间估计{t (i), xnoise (i)}™= 1比的情况下甚至更复杂的间距。使用平方和的最小二乘估计,
年代(r) = ^ [Xnoise (i) - exp {- [t (i) - t (i - 1)] / r}■Xnoise (i - 1)) 2
以得到目标为t估计量,r = argmin [S (r) j。最小化必须进行数值(2.7节)。等距离的t (i) - t (i - 1) = d Vi,情商的最小二乘估计量对应的估计量。(2.4),与一个= exp (- d / r)。
t的估计的偏差不均匀间隔的数据似乎藐视一个分析推导。图2.3显示了偏见通过蒙特卡洛模拟研究。模拟表明,偏差情况类似于价值甚至间距。
AR(1)模型的适用性不均匀间距可以评估使用残差,e (i) = Xnoise (i) - exp {- [t (i) - t (i - 1)] / r}■Xnoise (i - 1), 12 (2)
0.850.800.750.700.65 -
图2.3。蒙特卡罗研究偏差的自相关估计AR(1)过程中,已知的意思是,不均匀间距。时间序列生成Eq。(2.9)与n = 50 t = 1 / ln(0.7) ~ 2.804通过随机数生成器(2.7节)。一开始将T (1) = (1) = 1;间隔,d (i),是来自与一个预定义的伽马分布有序参数(2.7节),随后扩展,t (n) = 50 d = 1。“等效自相关系数”是一个= exp (- d / T) = 0.7。标准差的间距,广告,被用作衡量的不均匀。每次网格(广告固定),数字(nsim = 10000)时间序列的生成和Eq后确定。(2.11)。(打开显示符号)的平均数量exp (- d / r)在模拟。也显示(填充符号)估计的平均值是2.4 (Eq)应用于线性插值,等距时间序列(同样的开始和结束,同样的数据大小)。 (The standard error (~ 1/^/nsim) of the estimation averages is smaller than the symbol size.) The true autocorrelation value (solid line) is underestimated by the r estimator. This negative bias is excellently described by the bias approximation (dashed line) of White (1961) from the case of even spacing. The interpolation, on the other hand, leads to serious overestimation. This effect is owing to the serial dependence introduced by the interpolation (Fig. 1.13), it increases with 2.1.2.1嵌入在连续时间 在连续时间,AR(1)噪声模型是在“微分符号” dXnoise (T) = a•Xnoise (T) dT + dW (T) (2.13) 其中一个是自相关参数,dT是时间增量,dW (T)是一个创新的维纳过程(也称为布朗运动),W (T)。离散时间模型,连续时间AR(1)模型具有指数衰减的自相关函数(普利斯特里1981)。 让我们考虑到连续时间采样噪声模型在离散的时间,这可能是间隔不均匀,导致离散时间模型,{T (i), Xnoise (i)}™= 1。罗宾逊(1977)表明,> 0,这导致等于离散时间模型AR(1)模型在Eq。(2.9)。离散时间AR(1)模型嵌入到连续时间,它决定了独特的底层连续时间AR(1)模型在Eq (2.13)。这是一个重要的AR(1)模型的属性,因为嵌入允许基础物理,工作在连续时间(微分方程)。 2.2二阶自回归模型 我们甚至认为间距和编写离散高斯二阶自回归AR(2)噪声模型, Xnoise (i) - a1•Xnoise (i - 1) + a2•Xnoise (i - 2) + E(我),(2.14) E(我)是一个静止的纯随机过程(没有串行依赖)。这个AR(2)过程不是完全静止的,但条件a1和a2,只有渐近稳定(它的时刻我^饱和的方法);参见2.6节。区域的渐近稳定性a1a2飞机图2.4所示。的行为AR(2)过程的自相关函数取决于a1和a2所在。a2 > - af / 4, a1 > 0和a2 < 0, p (h)衰变顺利为a2 0 > -a2/4, a1 < 0和a2 < 0, p (h)交替信号衰减。在连接与光谱分析(第五章),这个案子a2 < - af / 4是有趣,因为p (h)显示除了衰变quasi-cyclical行为一段,因为(0)- a1 / (^ a2)。图2.5显示了一个实现过程的Eq (2.14)。 常用的AR(2)模型的估计包括Yule-Walker估计, =¡5(1)■[著名1 - 5 (2)]/ [1 - p (1) 2) 02 = [5 (2) - p (1) 2) / (1 - 5 (1) 2) 在哪里 继续阅读:Sejj [Cjj12 421 这篇文章有用吗?