英国南极调查高交叉Madingley Rd英国剑桥CB3 0等

82.1介绍
估计床地形和基底滑溜间接通过影响表面形状和表面速度是一个逆问题的一个例子。如果我们把所有可用的表面测量向量y,表示基底属性通过x,和床之间的关系和表面写成y = f (x), f是转发模型,逆问题是确定条件概率分布函数(PDF);P (x | y))的系统状态的测量向量。这个PDF也可以写成P (b, c |年代,u, v, w), b和c床地形和基底滑溜,分别和s, u, v和w三个组件的表面形貌和表面速度矢量。
远期f模型很可能没有通常意义上的逆。举例来说,我们可以认为,对于一些x, f (x) = 0,表明一些属性床的表面上没有影响。然而,使用贝叶斯定理,这个条件概率也可以写成
P (y)和P (x)是测量向量的先验概率密度函数和系统状态,分别和P (y | x)是有条件的PDF y给x。而不是试图找到f的逆,一般不会存在,我们使用贝叶斯定理计算P (x | y) P (y | x)。假设pdf是高斯和转发模型可以线性化,y = Fx e + e, F是一个矩阵和测量错误,采取上述的负对数表达式和最大化对x导致最大后验的反问题的解x x = xa + RaFH (FRaRH +重新)1 (y - Fxa)
在xa的先验值x, Ra和xa和e的协方差矩阵,分别上标H表示共轭转置(罗杰斯,2000)。上面的方程给出了一个估计系统状态(x),可以解释为一个加权和的先验(xa)和新信息系统状态所获得的测量(y)。
82.2提出的问题
提出的问题包括确定表面形状和表面速度给定的床地形,基底滑溜和本构方程的形式。要解决的方程是aijj + fi = 0,和vij = 0 aij对称柯西应力张量的分量,vi是速度矢量的分量和fi体积力的分量。笛卡儿坐标系统是使用x和y轴跨越水平面,和z轴向上翘着。本构定律格伦流定律压力指数n。边界条件上的运动学边界条件(s = s (x, y))和低(b = b (x, y))界限,自由表面条件上边界的压力和滑动法,乌兰巴托= c (x, y)结核病,沿着下边界,乌兰巴托基底滑动速度,结核病基底剪切应力和c (x, y)基底滑溜。这个问题是非线性的,因为n ^ 1本构律法是非线性的,因为表面字段以非线性的方式反应有限扰动在床地形(b (x, y))或基底滑溜(s (x, y))。
的长波提出解决方案的敏感性变化在基底属性可以为非线性流变学分析确定。任意长度尺度,解析解存在线性流变学和数值解非线性流变学(Hutter, 1983;Reeh, 1987;Johannesson, 1992;Gudmundsson, 2003;Hindmarsh说他是雷蒙德et al ., 2003年,2004年)。在这两种情况下表面形貌的扰动
(s (x, y))和表面速度(u, v, w),在频率空间相关传输函数,解析表达式的存在(Gudmundsson, 2003)。这个关系可以书面形式y =外汇,y是一个向量包含所有表面的测量表面形貌和表面速度,x是一个向量包含需要预计基底滑溜和床地形,与传递函数F是一个矩阵的元素。
82.3逆公式
反问题在于确定条件概率密度最大的P (b, c |年代,u, v, w)和协方差最大的b和c,鉴于表面数据和相应的协方差矩阵。如果表面形貌的测量和测量组件是独立的,每个表面的速度和床地形独立滑溜的分布、P (b, c |年代,u, v, w)可以写成8 pdf的产物。每一个PDF给一个表面变量的条件概率(s, u, v, w)对一个未知的基础变量(b, c)。表面和基底数量(s, u, v, w, b和c)被认为是安排在列。假设所有pdf是高斯,最大化的负对数的产品对b和c导致b - (Rb) 1 (FHR-e + FHuR-lu + F % r y + FWR-1w)
Fs是相应的模型(例如s = Fsbb), b是向量给在每个网格位置和高度吗
- FsbRseFsb + FubRueF
估计滑溜的分布(c)是相同的形式,但在所有下标c取代b。保持简单的符号已经假定床和基底滑溜的先验值都等于零。
上面的表达式给出了解决方案作为x和y的函数。用传递函数公式,表面数据必须转换成频率空间。这通常需要表面数据插入到一个等距网格。这将导致插值错误和一些空间插补值之间的相关性,两者都必须估计。最优插值方法可用于这一目的。表面形貌,例如,我们寻找的形式估计年代- Fs + e, F是现在未知矩阵决定。无偏最小方差插入器是由年代' = ssa - Rsa (Rsa + Re) 1和插值数据的协方差矩阵R的= Rsa - Rsa (Rsa + Re) 1 Rsa。Rsa covari-ance矩阵的分析,可以确定实验变差函数(Kitanidis, 1997)。傅里叶变换的插值结果字段和协方差矩阵导致估计拥有相同的形式上面给出的,但与,例如,年代由Ws和Rs WRsWH代替,W是离散傅里叶矩阵。如果噪音和先天的字段是不相关的,相应的协方差矩阵的对角形式和上面给出的表达式可以大大简化。
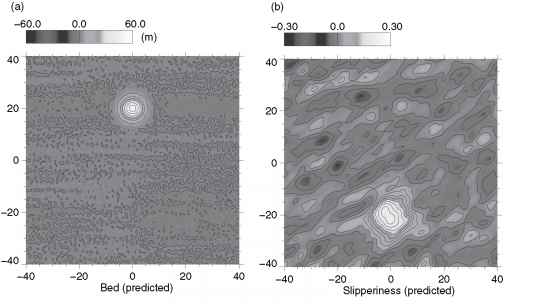
图82.1检索床地形和基底滑溜分布。x和y轴上的单位公里。上面的图的等高线间距是7.5米和0.025米的图。(见www.blackwellpublishing.com/knight彩色版本。)
图82.1检索床地形和基底滑溜分布。x和y轴上的单位公里。上面的图的等高线间距是7.5米和0.025米的图。(见www.blackwellpublishing.com/knight彩色版本。)
82.4应用程序示例
作为一个例子为床上同时反演地形和基底滑溜,合成表面数据生成使用高斯摄动床地形,slipperi-ness分布。提出问题,30%不相关的噪声是添加到解决方案和地表数据然后倒。图82.1显示了检索床地形和基底滑溜分布。(总)基底滑溜扰动是疾病预防控制中心,其中C是基底滑溜的平均值和直流微扰(部分)。图82.1 b显示了等值线的分数微扰(DC)检索。在图82.2中横截面沿y轴给最初的振幅之间的比较(虚线)和检索(实线)的扰动,左手代表滑溜扰动峰值和右边的床上扰动峰值。

图82.2横截面沿x = 0线在图82.1显示检索到的协议(虚线)和原始床属性床地形(右峰)和基底滑溜(左侧山峰)。(见www.blackwellpublishing.com/knight彩色版本。)
图82.2横截面沿x = 0线在图82.1显示检索到的协议(虚线)和原始床属性床地形(右峰)和基底滑溜(左侧山峰)。(见www.blackwellpublishing.com/knight彩色版本。)
继续阅读:Palaeoice板卷和长期的风化区山
这篇文章有用吗?