使用一个力平衡计算基底剪切应力

第一个近似,基底拖可以从rb = pgha(估计或结核病= Sfpgha吗山谷冰川)。然而,如果纵向力量不平衡,rb可能大于或小于pgha。例如,在图12.7中,身体力量,pgh,下坡的组件,pgha。此外,还有纵向力F和Fd。如果傅> Fd,长度所显示的箭头人物,rb显然将必须大于pgha为了平衡的力量平行于床上,反之。现在我们更详细地探讨这种影响。第一部分的开发是一个三维的泛化方法提出了b·汉森(胡克和汉森,1986,p . 268)。

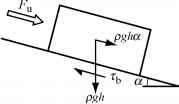
图12.7。纵向力一段冰川在一个倾斜的床上。如果傅> Fd基底阻力将大于pgha,反之。

x表面

图12.8。坐标系统中使用的力平衡分析。

因为我们的目标是计算阻力对冰川的床上,动量平衡方程(方程(9.32 b))是明显的分析的起点。要使用的坐标系如图12.8。x轴是水平和流动的方向,z轴是垂直的。写出动量平衡方程在x和z方向,记住阿^”=橙汁-帕克,导致:

dx, dy dz dx和doxz doyz做' d P

O + ~ oyL + f1 + T”=使用(12.24 b)

dx, dy dz dz

过程现在将解决方程(12.24 b) P,把结果代入方程(12.24)和集成的深度获取oZx (z = h)(=结核)。

求解方程(12.24 b) P,分离变量和z积分深度:

z z z z z

/ dP = -我——dz-1 dz -我做!——我pgdz J d x dy J zz™0 0 0 0 0

或者,指出P = 0表面:

z z

/ f d&yz doxz。。

dz -我dz -一个„„+ z-o - pgz d x J dy zz zz

现在水平导数,假设Bazz / dx \ z = 0是微不足道,指出dz / dx =一个,并把结果代入方程(12.24):

z z da”davr dazx d2axz f d2avz哒”

+ - v - + - -XZdz - - dz - zz - pga = 0

方程(12.25)的名次是强调atany givenlevel, z,在冰川,而我们感兴趣的是加法的压力随着深度获得rb。因此,仅仅指出,我们对深度积分:

0 0 0 h z d2axz d2avz dzdz——pgha = 0 (12.26)

显然,azx (z = h) (= rb)将获得积分第三项,最后一项是熟悉的pgha。然而,一些简化显然是可取的。

二重积分项的方程(12.26),有时也称为T-term,很难解释。在二维空间中,巴德(1969,第116页)已经表明,它可以近似:

和Whillans范德维恩准备研究(1989)认为,这一项有关“桥接”效应,压在床上的不同空间由于床上违规行为的影响,尤其是,空泡形成。因为冰是“软”,他们认为,这些桥接作用应该小而平均正常压力。因此,他们忽视的T-term力平衡的计算,我们应当遵循他们的领导在这方面。但他们承认,这样的“物理意义”“不是概念上简单”。

把第一项的方程(12.26),可以消除'zz指出,由于偏应力和应变速率之间的比例,不可压缩性条件,sxx + % + ezz = 0,导致+一个'yy + 'zz = 0。此外,因为azx将零自由水平表面,并仅略不同于零轻轻倾斜的冰川表面,在方程(12.26)是第三项所需的基底拖,rb,只是指出。与这些修改,方程(12.26)

就变成:

h h f dx + O + dz / iyrdz + rb-pgha = 0 (12.28)

为这个关系得到一个直观的感觉,考虑的情况“xx和ayx独立于深度和“yy是微不足道的。方程(12.28)可以减少:

pgha -结核病= 2 d0xxh + d0yxh (12.28)

dx dy

在二维空间(oyx = 0),这个方程表示,如果驱动压力、pgha,超过提供的拖床、结核病、拉伸率(exx aXx)将增加downglacier (da 'xx / dx > 0),反之右边第二项考虑谷面剪应力。(调整中我们忽略了桥接效果和z方向正面向下,范·德·维恩方程(12.28)是相同的和Whillans(1989)方程(12.25)。我们的发展遵循他们的。)

我们现在的目的是表达方程(12.28)的形式,使评价结核病从冰川表面应变率的测量。为此,我们注意到,因为1 = (e1 B) n - 1

流法可以写:

n - 1×2×1, e n;

插入在方程(12.28),扭转的分化和整合,并重新安排方面收益:

结核病= Pgha - - (2 exx + Syy) dz - eyx dz (12.29)

和Whillans范德维恩准备研究(1989)开发了一种数值程序进行深度集成,z。然而,对于简单的应用程序我们假设应变率无关的深度,以有限差分形式和表达方程(12.29),因此:

(2 exx + eyy) h我dwn uj

这里的符号| dwn, | | rgt, |融通的参考,分别downglacier和upglacier结束,和左右(downglacier看),“块”的Ax长度和宽度Ay的冰川。

表12.1。力平衡计算

时间

Sxx (dwn), 2 * 1项,kPa Term3 *, kPa结核病,kPa作为%

块一个冬天1983年7月1983年7月1984年5月1984年6月1985年6月

块B冬季1983年7月1983年7月1984年5月1984年6月1985年6月

0.006数据不完整数据不完整的0.000 -0.002 0.002

0.008

pgha 115 kPa块下面的值和145 kPa下块B。

“条款2和3是右边第二和第三项的方程(12.30),纵向和横向角度,分别。

右边第二项代表了对结核病的贡献力量的不平衡块的两端,而第三代表了双方的贡献力。

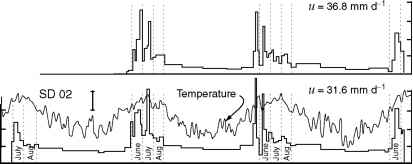
的一个示例应用程序提供的这个过程是一个实验进行Storglaciaren,瑞典(胡克et al ., 1989)。一些股权冰川表面(图12.9)经常进行调查在1982年和1985年之间确定速度(图12.10)。股份的模式,纵向和横向应变率可以计算upglacier和downglacier结束的“块”标记在图12.9 A和B,和剪切应变率可以计算沿两侧。计算结果六个时间如表12.1所示。一个时期代表的意思是冬天条件;结核病是-82 kPa下块和-92 kPa下块b,其他五个时间段是那些在高速发生(图12.10)。在这些事件中,结核病是降低平均近30%下块下a块B结核病是变量的变化,但发生在两个事件明显增加。

研究表明,物体的加速度变化的模式是,在每一个情况下,伴随着增加的大小

,Tarfala

*站

,Tarfala

*站

图12.9。Storglaciaren地图显示广义表面和床地形(分别为固体和虚线轮廓),股份用于速度测量的位置,速度,和块用于力平衡计算。(数据从胡克et al ., 1989年,图1。基础地图由彼得简颂。)

30 60

SD 05

标准错误调查7 d

SD 05

标准错误调查7 d

30 60

10 e

1982年

1983年

1984年

1985年

图12.10。时间序列的均值水平速度的三个应变钻石(SD)如图12.9所示。速度的平均值的4(或5)每个钻石的股权。平均每日温度,使用五天的移动平均平滑,底部面板所示。(修改从胡克et al ., 1989年,图3。复制国际冰河学协会的许可。)

10 e

1982年

1983年

1984年

1985年

图12.10。时间序列的均值水平速度的三个应变钻石(SD)如图12.9所示。速度的平均值的4(或5)每个钻石的股权。平均每日温度,使用五天的移动平均平滑,底部面板所示。(修改从胡克et al ., 1989年,图3。复制国际冰河学协会的许可。)

学期2(右边第二项在方程(12.30))。应变速率的数据,可以看出,在upglacier块exx变得不那么压结束时,在两种情况下,即使延长,同时downglacier结束它变得更加压缩在一个案例中。因此,加速度并没有由于downglacier从upglacier推或拉。显而易见,他们的结果减少电阻拖在床上,大概增加水压力引起的。

在块B的情况下,应变速率的数据表明,任期2中的显著变化反映了推动upglacier, 1984年6月的事件,从downglacier拉。这种推和拉的结合导致了更高的应变率在基底冰,因此,由于应力和应变速率之间的比例,提高基底阻力。

因为我们假定应变率均匀,结束的街区,也由于其他不确定性计算,获得结核病只是估计的值。然而,类似的错误可能是大小和符号计算,结核病的方向和近似的大小变化可能是可靠的。这些计算从而帮助我们理解机制

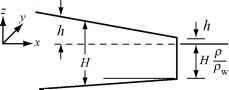
海平面

图12.11。坐标系统的讨论中使用浮动冰架。

的加速度发生在这些实例。通过这样的分析,我们可以了解空间和时间变化因素控制速度的冰川。

继续阅读:蠕变的浮动冰架

这篇文章有用吗?

0 0