累积应变计算

为了计算冰川的累积应变，首先必须知道速度场。然后计算冰粒穿过冰川的路径，以及路径上离散点的速度导数。为了得到冰从一个点移动到另一个点时的增量应变，然后根据速度导数计算应变率，并乘以移动所需的时间

(a)粒子路径和等时线

除T020

(b)最大累积延伸方向

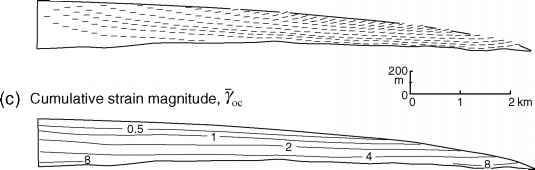
图13.5。(a)从文中所述的速度场计算出的粒子路径。等时线的年龄以年表示。(b)沿(a)中粒子路径以200 m间隔的条形显示的最大累积延伸方向方向。(c)焦点等值线。(摘自Hudleston and Hooke, 1980，图6和图7。转载已获爱思唯尔科学出版公司许可。)

图13.5。(a)从文中所述的速度场计算出的粒子路径。等时线的年龄以年表示。(b)沿(a)中粒子路径以200 m间隔的条形显示的最大累积延伸方向方向。(c)焦点等值线。(摘自Hudleston and Hooke, 1980，图6和图7。转载已获爱思唯尔科学出版公司许可。)

(Ramsay and Graham, 1970，公式7-10)。最后，将这些增量应变相加，得到累积应变。

Hudleston (Hooke and Hudleston, 1980;Hudleston和Hooke, 1980)利用巴恩斯冰帽上流动线上的速度和质量平衡的综合数据进行了这样的计算，如图13.5a所示(另见图12.17)。为了估计深度的水平速度，他使用测量的表面速度，并调整式(5.7)中的B值，得到床层上的零速度，这里的温度远低于熔点。他没有使用测量到的垂直速度，而是使用质量平衡数据来估计地表的长期稳态垂直速度，并假设它随深度线性下降。横向应变率很小，所以他认为可以忽略。

他的计算结果如图13.5和13.6所示。通过从聚集区域的9个点开始跟踪颗粒，他首先绘制了9条流线(图13.5a)。然后他计算了

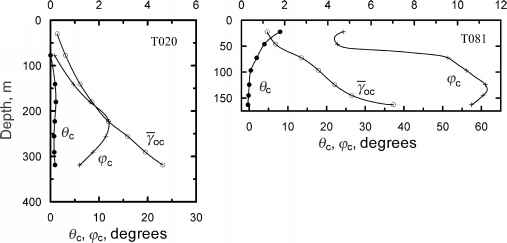
图13.6。巴恩斯冰冠钻孔(a) T020和(b) T081位置的yoc、yi0c和yc随深度的计算变化。钻孔位置如图13.5所示。(摘自Hooke and Hudleston, 1980，图8a和9a。转载已获国际冰川学学会许可。)

图13.6。巴恩斯冰冠钻孔(a) T020和(b) T081位置的yoc、yi0c和yc随深度的计算变化。钻孔位置如图13.5所示。(摘自Hooke and Hudleston, 1980，图8a和9a。转载已获国际冰川学学会许可。)

最大累积延伸轴的方向(x轴:图13.5b)。在这张图中值得注意的是，这些轴几乎平行于整个冰川床的事实。T061钻孔附近和冰川下表面的冰川上倾角增大是接近平衡线时单纯剪切与纯剪切比值增大的结果。如前所述，在简单剪切中，最大伸长轴最初下降45°;随着变形量的增加，它逐渐旋转到与剪切平面平行。

累积应变幅值yoc如图13.5c所示。这些数字看起来并不重要，直到人们意识到yoc与应变椭圆轴比的自然对数成正比。因此，在最基底冰中发现的yoc = 8，对应的延伸率为~18 000:1。一个1米的立方体会被拉伸成1米宽、134米长、7.5毫米厚的缎带!

图13.6显示了T020和T081钻孔中yoc、0c和yc随深度的变化(图13.5a)。由于T020的主要应变模式，特别是冰川上部的主要应变模式，几乎是纯剪切，垂直压缩和纵向伸展，最大累积伸展轴几乎是水平的。因此，0c仍然接近于0。另一方面，yc在表面为0，最初随着du/dz的增加而逐渐增加。但随着冰川深度的增加，到达T020的冰所经过的区域越来越大，以纯剪切为主(图13.4)。因此，

T081钻孔现场的格局在几个方面有所不同。由于这个洞位于消融区域的上部，表面的冰在从冰川的高处移动时积累了一些应变。因此，Yoc > 0在表面。随着深度的增加，冰移动的距离越来越远，积累的应变也越来越大，因此Yoc增加到7左右，代表轴比超过5000。由于靠近地表的冰经历了少量的混合简单剪切和纯剪切(图13.4)，这里的0c«10°和

为了进一步量化纯剪切早期历史的影响，Hudleston计算出完全由简单剪切产生的总应变Yoc为3.75的冰粒的

现在让我们用我们对累积应变的理解来研究生叶．

继续阅读:叶理成分

这篇文章有用吗?

0 －2