组件的绿叶
冰川的明显的带状特征(见,例如,图5.18和8.8),导致相当大的混乱。条带消融区最显著的一次冬天雪融化。然而,条带也可能出现裂缝的墙壁聚集区,尽管它有一个非常不同的外观和大多数人会正确,将它称为年度分层或沉积分层。分班是通常近似平行的最近的边界表面,无论是床上,谷壁表面,或。然而,在下部的消融区通常缓缓急剧upglacier(图13.7 b)。带透射;也就是说,乐队是层冰的横截面。
仔细观察,发现带状外观最常见的结果从泡沫或污垢内容的变化。后者,加上暗示upglacier倾斜的边缘附近的乐队,引发了错误的印象,条带反映剪切飞机在冰碎片(以某种方式)进行
150 100
距离,m
300 200 100
距离,m
跟踪和测量倾角的叶理|钻孔
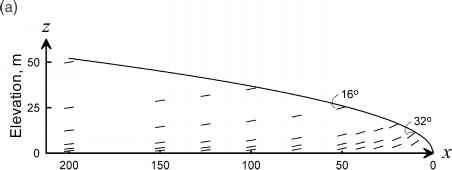
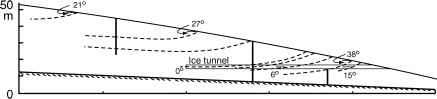
图13.7。(a)叶理的态度的一个理想化的完全塑性冰川抛物线表面轮廓。看到文本的解释。(b)的横截面的巴恩斯冰帽显示下降的叶理飞机冰表面的测量,隧道挖掘的利润。虚线显示叶理的痕迹从测量飞机的下降和核心地层学。
表面。很少会出现这种情况。延长泡沫和,在某些情况下,拉长晶体可能导致带状的外观。
叶理的最终产品是对任何起源的非均质累积拉伸和剪切等菌株本章的第一部分中讨论的。这样的待遇后,最初的不均匀性是不可能的起源是显而易见的。例如,假设1米立方体我们前面提到的是米开朗基罗的雕塑材料的流变学类似冰。我们认识到它后,变成了带长135米,7.5毫米厚吗?也许我们可以确定材料,但肯定不是原来的英俊的形状。
所以导致叶理的尺度是什么?最明显的是裂缝的沉积分层,你只能看到墙上的聚集区。这个分层定义为粒度的变化,尤其是基地附近的一个年度层深度灰白色形式。飞尘从无雪地面在融化季节通常较年度层的表面,和渗透,冰层融化的融水可能传播视野所定义的变化雪密度,形成相对没有气泡的镜头。都为层状外观。Gland-shaped身体重新冻结的冰也可能形成渗透融水(p。20)。模式的伸长方向如图13.5 b,很明显,这些尺度将垂直纵向拉伸和压缩。因此,变形强调了最初的分层。时出现非均质低消融区,他们将没什么相同之处原始沉积分层或腺体结构。一旦这样的尺度变形超出识别做好准备,可以恰当地称为绿叶的结构。
另一个主要组成部分层面理裂隙填充物。雪被风吹积成裂隙在冬季和夏季融水可能饱和这雪。当裂缝被搬到一个位置,或旋转成一个取向,强调在它compres-sional,关闭这填充被压扁。一个乐队因此形成交叉削减沉积分层或叶理来自这样的分层。最初,这横切关系是显而易见的,可以正确地认定为是什么,即使它交叉削减叶理的起源不能确定。然而,一旦进一步填充被压扁,旋转至接近与其他绿叶的并行性,拉伸,它的起源将不那么明显。然而,仔细观察仍然可以检测的横切关系。
另一个重要组件基底冰的绿叶的碎片。正如我们已经讨论的,有各种机制的碎片可能在基底冰变得越来越大——重新冻结的部分复冰周期,冻结的机制讨论罗宾(图7.6)或地区温度梯度在基底冰导致当地重新冻结(图6.12),片冰中夹带过量下蚀作用(图8.33),等等。在所有情况下,由此产生的平行层床或峡谷墙壁和在高的地区,简单的剪切。层的确切起源之前很难确定变形,剪切任务通常是无望之后,虽然化学和同位素签名可以帮助(Souchez Lorrain, 1978)。
生叶边缘区
我们上面所提到的,绿叶在冰川边缘经常被误认为是所谓的“剪切飞机”,大概是最大剪切应力的平面平行。在这里,我们表明,upglacier浸叶理的冰川表面方向的最大剪应力几乎没有联系。
在图13.5和13.6的情况下,第一个任务是确定速度场。然后我们使用速度场,看看绿叶,近平行于床上一些边缘的距离将变形是被动地流水。
我们采用的坐标系原点在保证金,x轴是水平和指导upglacier沿着床上,z轴是垂直向上和积极的(图13.7)。我们假设:(1)概要文件的冰面边缘区可以用h = * Jcx近似,h是地表高程,x是边缘的距离和c是一个constant1;(2)烧蚀率、bn(负数),在感兴趣的领域是一致的;(3)配置文件是一个稳态概要文件与bn = - w +我们谭(方程(5.26));(4)水平速度,u,独立于深度;(5)二维应变(平面应变);(6)冰是不可压缩的。消融downglacier失去的冰量从一个位置x然后bnx过去x,这必须等于质量流量或哦。因此,
Q = bnc1/2的地方。(bn是负的,问是负的。这是符合你的消极的方向。)不可压缩性的假设可能是由:
微分方程(13.7)和使用结果积分方程(13.8)的收益率:
我们现在确定的冰元素的坐标作为时间的函数。元素的开始位置(xo,佐薇)在时间t = 0。u = dx / dt,方程(13.7)可以集成获得:
x = (xy2 + 1 Qt) 2 (13.10)
1这个方程,首次导出了奈(1951),可以获得的积分方程(5.2 c)
= dh / dx。读者会发现,c = / 2 azx / pg。
然后结合方程(13.9)和(13.10)eliminatex,指出w = dz / dt,我们获取和集成:
继续阅读:基本运动波理论
这篇文章有用吗?