基本运动波理论
现在让我们分析开发这些想法。在这个发展,奈(1960)的分析后,我们认为一块冰坡,3 (x)与厚度、h (x, t),和地面坡度(x, t)(图14.2)。我们假设dh / dx是小,板在水平方向上无限扩展的正常x轴。地面坡度与床坡度:
-
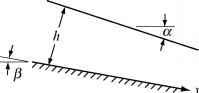
- 图14.2。地面坡度之间的关系,床上斜坡,p,和厚度,h。
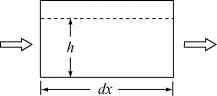
图14.3。贡献质量的变化在一个元素的冰川长度dx。
注意,如果h减少downglacier d h / dx是- > p。
考虑在一个元素质量守恒的冰川长度dx(图14.3)。为了方便起见,我们将表达质量通量的等效的冰,基于一个标准密度。冰流入元素的速度,q (x, h, t),和速度,q + (d q / dx) dx。这里,问是冰川的通量单位宽度,因此m3a-1m-1维度。此外,还有积累bdx速度。如果更多的冰流,或者积累,元素比叶子,冰川厚度的增加速度(dh t / d),所以冰的体积增加的元素(dh / dt) dx。因此:
或者,简化:
因为q是h和x的函数,方程(14.2)表达的功能依赖导致一个一般类的运动被称为流系统运动学波(《和Whitham, 1955)。我们的下一个目标是获得一些对电磁波在冰川的本质。
让我们首先考虑到波速度。假设我们方程(14.2)两边同时乘以(dq / dh) x = c, c在哪里通量的变化造成x点厚度的变化,因此:
问d d h d d q为c_I + =公元前公元前或c - + = (14.3)
dx d h dt dx dt
图14.4。数值在方程(14.3)的解释术语。
1050年
1050年

100米
1000年
100米
方程(14.3)被称为运动波方程;c维度m3a-1m-1 / m = ma-1。因此,这是一个速度。事实上,它是敏捷(或速度)的波。(因为q =呃,u(泥沙)平均速度,dq / dh = u + h (du / dh)。)
获得一些对方程(14.3)的影响,考虑情况如图14.4所示。冰川冰通量的元素是1050 m3a-1m-1,虽然这是1000 m3a-1m-1。元素是消融区和烧蚀率是-0.4 a - 1,或-40 m3a-1m-1元素的长度。由于这种积极的平衡,有冰进入元素比离开它,冰川厚度增加。使用ofEquation(14.3)我们可以计算质量流量的增加,dq / dt,造成这种厚度的增加如下。通量梯度,dq / dx, 100米长的元素- 50 m3 a - 1 m - 1 / 100铁道部-0.5 a - 1。假设c = 200 ma-1。然后,dq / dt是20 m3a-1m-1。换句话说,由于厚度的增加和由此产生的增加速度,质量通量增加20 m3a-1m-1。
q之间的关系,h, u,如图14.5所示,在q是策划针对h。由于非线性流的法律,我们希望问增加非线性h如图所示。平均速度,u,冰川的冰厚度和通量的q和在点P h值图是u = q / h。这是用虚线连接P的斜率与原点。然而,速度,c,运动学波(d q / d h) P,这是一条线画的切线的斜率q-h曲线在点P .换句话说,正如前面提到的,运动波的速度明显比冰川的平均速度。
了解如何更快的运动波移动时,考虑的情况下冰川移动完全由内部变形这样,方程(见5.19):
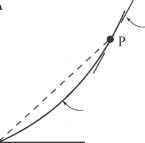
图14.5。平均速度的关系fdq \ \ dk的冰川和速度/ d运动波。
基于流法
图14.5。平均速度的关系fdq \ \ dk的冰川和速度/ d运动波。
基于流法律问
c = dh = 2 (ff) V1 = (n + 2) u (14.5)
换句话说,运动波移动的速度大约是冰川的泥沙速度的5倍。如果有基底滑动和滑动速度变化t2(方程(7.10)),这个比例可能会略低于5。这个关系,严格,无穷小。一波又一波的有限振幅可能更高的速度。
这篇文章有用吗?
