在冰川等势面

渗透多孔介质,水流的方向负梯度最大的潜力,美元,美元被定义为:

在这里,o是一个参考电位,美元Pw的压力水,Pw是水的密度g是重力加速度,z是海拔高于海平面等基准面。

获得一些对这个概念,考虑这种情况在一个湖泊(图8.2)。让= 1点1美元在湖上表面。向下移动一个距离Az 2增加Pw pwgAz但减少右边的第三个任期相同数量在方程(8.1)。因此2 = 1美元,没有点1和2之间流动。然而,如果湖

图8.3。在稳定状态下,关闭一个圆柱形管道,u,被融化,平衡。

斜坡表面轻轻向出口,将水平恒定z = z2从2点到3点会导致减少在Pw,因此流将朝着低Pw的位置,这也是一个地位较低的美元。换句话说,它不是Pw的梯度控制流的方向,但在美元梯度。

确定势场冰川从方程(8.1),我们必须确定Pw无处不在。Pw不是静水,因为水是移动,和大多数是很长的路从表面到许多小的段落。

一般来说,压力在冰上,π,不同于在水中,这个压力差的冰变形结果。Pw很少超过π显著,但它可以远低于π。段落可能因此增加的大小稍微在非常高的水压力,大小以低压力迅速下降。此外,如上所述,粘性耗散所产生的热量融化管道墙壁,扩大通道(图8.3)。在一个稳定状态,关闭通道的蠕变冰,u,等于熔化率,m,所以的净增长率大小的段落,r = m - u = 0。(尽管在数学上不整洁,注意,我们定义了积极u是内在的,而积极的m是外在的。这简化了一些后来方程。)

让我们假设,流ofice可以representedby se = (e / B) n,冰是不可压缩的,各向同性,段落是圆形截面。我们进一步定义的压力导致蠕变关闭,Pc,通过:

(图8.3)。一个好的近似,π=猪(H - z),他以上的冰面高程基准水平(图8.4)。然后:

(奈,1953)。这个关系将在第12章中(方程(12.22))。在推导假设ae = (l / v ^ ^, ^径向应力偏量。换句话说,devi-atoric应力张量的其他组件,应变率张量,因此,被认为是微不足道的(见方程(2.10))。因此,不可能有变形造成的以外的冰的存在。在当前应用程序中,这种假设显然是违反,我们添加一个乘数,K,这大约是1。K = 1如果ae = ^ (1 / * Jl)。重新排列和代替Pc和π,我们可以把方程(8.2):

冰的表面

图8.4。坐标轴的讨论中使用管道关闭。

(如果你< 0,这意味着通过开放的水压力超过冰压力,必须使用| | u,第二项的符号进行相应的调整,但u < 0在本质上是罕见的。)超过几公里的冰川末端,参数在右边的上学期变化沿着隧道相对较少。因此,结合方程(8.1)和(8.4),对任意方向的导数,年代,收益率:

ds游戏机ds

确定方向的等势面冰川,我们利用这一事实如果s在于这样一个飞机,9美元/ 9 s = 0,所以:

——(Pw - PU ~ =π- d d年代

我们的目标是定义这个平面的倾角,¡3。蘸一些水平方向,x,将dz / dx,因为z的垂直坐标平面上(图8.5)。因此,方程(8.6)乘以ds / dx和重新排列,因此:

Pw -πd s d x,或者插入各自的密度数值,让= dH / dx,冰川表面的斜率,并指出tan p = dz / dx:

因此,等位飞机倾斜upglacier(注意负号)坡约11次冰川表面的斜率(图8.6),获得的结果首先施立夫(1972),和水进入冰川通过冰川锅穴应该达到的床冰川距离downglacier入口点。支持这一点,Iken和宾德谢德勒(1986)发现,压力波动Findelengletscher水井钻到床上,在积雪下面,没有与河川径流的变化进入附近的莫林。相反,压力波动似乎反映出慢延迟输入的水通过上面的积雪积雪边缘。

dx dx dz

图8.5。倾斜的管道显示ds和p是如何定义的。

图8.5。倾斜的管道显示ds和p是如何定义的。

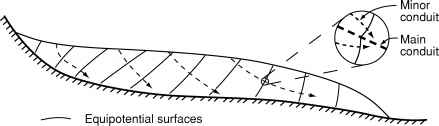
50 m L近似规模100 m

图8.6。纵切面的冰川显示upglacier-dipping等位面和冰川内部的水流的理论方向。插图显示了造窝的等势面和顺向的流在较小的段落主要渠道。(胡克之后,1989年,图1)。

严格的等势面定义只在水通道,但适当的谨慎,他们可以被视为尽管定义整个冰川。因为Pw < P{在正常情况下,O是略低的管道比周围的冰。因此,等势面带酒窝的附近的管道。O降低downglacier,酒窝点upglacier如图8.6所示。使用下面的理论,它可以表明,π的区别和Pw管道尺寸增加而增加,所以酒窝更大的渠道更大。因此,水在较小的管道流动正常等位表面就会走向更大的偏移。这加强了导管系统进化的趋势朝着一个树木状的模式。

equipotential-plane倾斜的替代来源

考虑到情况如图8.7所示。之间有一个水管在床上点1和2。我们想确定在什么条件下的upglacier坡山将平行的等势面,这样水管道不会流。冰压力(1)Pi1 =猪(h1 h2 + +啊),(2)皮= pigh2。在没有水的流量和管道关闭,水的压力(1),Pw,将皮的总和加管道的静压头,pwgh1。如果软件> Pw,管道就会开始缩小和水将被迫在山上。因此,我们所寻求的条件是软件- Pw,或者:

πg (h 1 + h 2 +啊)- p gh2 + pw gh (8.8)

解决了h1,除以Ax,指出——啊/ Ax和褐色P - h1 / Ax,和插入数值密度直接导致方程(8.7)Q.E.D.

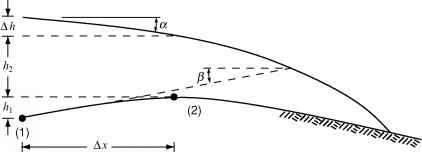
图8.7。示意图说明替代推导等势面倾斜的冰川。

继续阅读:沉积物供应蛇形丘

这篇文章有用吗?

0 0