冰下水管
在第8章中,我们将式(12.22)应用于冰下水管的闭合。如上所述,由于床上的阻力,当人们试图估计半圆形导管的关闭率时,问题就出现了。在试图估计宽而低的管道的关闭率时出现了更深刻的困难,因为冰中的应力不再对称地分布在管道周围。
在这里,我们研究另一个感兴趣的问题:半圆形导管边界处床上的正应力,特别是这些应力从导管向外的梯度(图12.6)。Weertman(1972)首先研究了这个问题。如果压力是
-
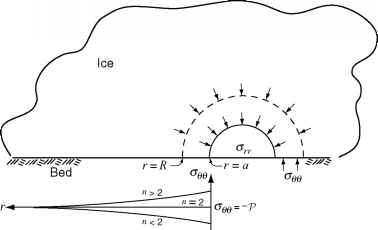
- 图12.6。半圆形导管周围的应力:orr是延伸的,ogg是压缩的(因此P上有负号)。ogg远离隧道的变化示意图显示。对于n > 2, ogg的压缩小于P,反之亦然。
较高的水管毗邻,水在膜处ice-bed接口将被迫离开导管,反之亦然。
这个问题的意义在于它对地下水流的应用极地冰原.有几位作者提出,在冰川表面没有水输入的情况下,要在这种冰块下面存在管道,就必须有来自床层邻近部分的水流入(Alley, 1989a;困境,1982;Weertman和Birchfield, 1983;Ng, 2000)。存在这种渠道的问题是根本的;在它们存在的地方,冰下水的压力可能会明显低于其他情况。因此,任何试图解释,例如,冰流的快速流动取决于对水流系统本质的理解。
这个问题的相关重点是ogg。因此,让我们从式(12.14a)中ogg的表达式开始。请注意,在这样做的时候,我们默认床是平坦和光滑的,这样剪应力就不会阻碍冰向隧道内的运动。oa的合适值现在是冰中的压力与管道中水的压力之差,AP。与之前一样,我们在每个地方都加一个压力,-P,以说明冰的重量。稍作调整,式(12.14a)可得:
ogg = - ap an r-2 - P (12.14b)
注意,ogg是负的,或压缩的,因为P总是超过右边的第一项。
由式(12.14b)可以看出,当n > 2时,ogg将无法支撑冰川的重量,此时ogg ^ -P as r ^to,但在导管附近有ee > -P。换句话说,一个ee有足够的压缩力来支撑远离管道的冰川,而不是靠近或下面的冰川。然而,a(rr = R)比a(rr = a)更有压缩力(式(12.17a)),这提供了额外的支持。也就是说,由图12.6可知,作用在地表半径R处的垂直力与作用在床层上的垂直力相等,即:2 /0(AP - P)dr + 2 /R(aee - P)dr。
现在让我们考虑一个半圆形的导管,在一个水平床上,在一个均匀的厚度和无限的水平范围的冰盖下。对aee沿床层对r求导,得到da ee 2 /n -2 \ 2 /-2,,\
- =- AP an r - (2+1) (12.23)
如果n > 2,就像预期的那样,daee /dr为负。因此,在远离隧道的地方,aee减小,或变得更负,或更有压力(图12.6)。在这种情况下,薄膜中的水将被迫流向导管,从而增强管内的放电。然而,当人们考虑耦合应力时,特别是在与管道平行的床上存在剪应力时,情况就不那么简单了。在这种情况下,水流似乎远离隧道(Weertman, 1972, pp. 299-300)。
da ee/dr随n变化的物理原因并不明显。我们可以预期,如果在冰川底部引入一个空腔,邻近空腔的压应力将会增加,以支撑冰川中不再被空腔下面的河床所支撑的那部分重量。但是,向隧道方向,u和err增加,这就需要增加a'rr。改变应力场以满足这一要求的方式,以及因此床上压力重新分布的方式,取决于n。对这一影响更直观的解释是难以捉摸的。
继续阅读:利用力天平计算基础剪应力
这篇文章有用吗?
