平均时间和光谱的差距

最后更新于太阳,2023年1月1日|热通量

热流值(4 x 106 (w 'T1))和95%置信区间的实现(图3.6)相差大大超过各自的误差。是很常见的看到大协方差值的变化从一个下半场各样本下即使在流是相对稳定的。这样做的原因是隐含在wT的时间序列图3.4,协方差是由一些大型的积极和消极事件与时间尺度的湍流漩涡分钟上下传热。如果一个样本包括过量或赤字几这些事件,它可能影响明显协方差值。因此采样策略代表一个权衡留在“光谱缺口”,实现平均时间会捕获大部分艾迪事件,但平均流量的速度和方向的变化不会影响协方差统计数据。一般来说,我们的方法是将流态划分为下半场实现充分的简化坐标代表实际的流,然后进一步平均协方差估计时间更长,通常1 - 6 h。使用个人实现引导的结果分析,协方差的置信区间较长时间可能是由调用中心极限定理(例如,出版和利伯曼1959),我们假设covari-ances决定每个下半场实现与已知方差正态分布。在这种情况下,即使有少量的样本(在当前的例子中,四个值{w的)真正的95%置信区间的意思是,与样本均值

MaudNESS湍流热通量、3 m

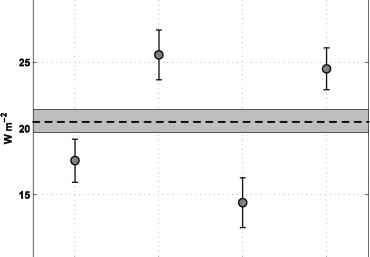
图3.6样本协方差图3.5乘以卡式肺囊虫肺炎将显热通量,以及置信区间是从文本中描述修改的引导方法。四个实现的虚线是均值(1 h)与阴影框表示1小时均值的95%置信区间

下半场实现:222.500至222.531

图3.6样本协方差图3.5乘以卡式肺囊虫肺炎将显热通量,以及置信区间是从文本中描述修改的引导方法。四个实现的虚线是均值(1 h)与阴影框表示1小时均值的95%置信区间在Xn n的样本均值实现协方差,并引导标准差的平均值。图3.6中的虚线是样本均值的四个协方差热通量估计,与相应的95%可信限阴影框所示。

上述过程也可以被应用来评估协方差估计的置信区间湍流应力t = (u 'w1) + i (v 'w”)。在这种情况下,有两个维度,置信区间在复平面跟踪一个正方形,在图3.7中所描述。

必须注意分配两个deviatory协方差的置信区间对应的时间序列湍流通量,主要是因为不确定性应用泰勒的假说,它严格地只适用于稳定流动。在实践中,很少有自然IOBLs不同稳定超过几个小时,和平均时间的选择“动荡的实现”可能显著影响的平均通量估计协方差的测量。一个例子从6小时期间MaudNESS漂移上面讨论说明了这一点。从0300年到0900年,2005年8月10日,冰漂移与适度的压力相对稳定。数据集被分为14个不同的实现产品的时间序列,w x T ',平均时间从1分钟(360

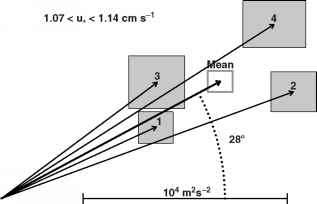
图3.7四下半场实现covaiiance估计压力:T = (u 'w”) + i (v 'w”),阴影框显示个人置信区间(u 'w)和(v 'w”),分别与均值和相关词框。真正的轴(水平)与平均流量的方向在每种情况下,应力矢量的平均偏差约28°逆时针。也列出一个置信区间的摩擦速度大小,从最小和最大平均应力的限制

图3.7四下半场实现covaiiance估计压力:T = (u 'w”) + i (v 'w”),阴影框显示个人置信区间(u 'w)和(v 'w”),分别与均值和相关词框。真正的轴(水平)与平均流量的方向在每种情况下,应力矢量的平均偏差约28°逆时针。也列出一个置信区间的摩擦速度大小,从平均应力的最小和最大限度实现)到1 h(6实现),和协方差,(w),平均每个实现整个段。结果与误差代表产生的平均协方差的置信区间(乘以卡式肺囊虫肺炎)图3.8所示。当实现间隔太短(< 5分钟)的协方差捕获在实现时间越长时间错过了,因为时间间隔与包含涡流的时间尺度的能量。与实现集间隔范围从6到20分钟,均值的置信区间值位于或接近标准下半场实现集(虚线所示)。然而实现更长时间的间隔(30 - 60分钟),平均值低了一个瓦特每平方米。

这个练习的目的是指出:从时间序列的协方差统计计算通量只是一个近似的统计平均值,取决于几个有点主观因素,包括实现间隔之间的权衡和长期时间环境的变化。主要基于经验无数这样的演习,我们通常使用15分钟为实现平均区间,并进一步平均这些至少1 h(四个实现)稳定通量估算。LeadEX却是个例外,能源的规模包含湍流漩涡的静态不稳定条件明显大于在不久的中立稳定条件(McPhee和斯坦顿1996)。在这种情况下,选择实现间隔是1 h。

平均热流:222:0300 222:0900

!
1 36美元
我“U24 _
	fl8 1	512年19	3	f®
			J	l
j > 90£120

180年


§360

10个20 30 40

平均周期,分钟

10个20 30 40

平均周期,分钟

图3.8的影响平均时间在湍流热通量计算的covaiiance devia-tory温度和垂直速度6小时时间。数字旁边的符号表示的数量实现在每一个平均水平。为每个平均误差表示置信区间,通过引导派生方法中描述的文本

继续阅读:混合长度涡流粘度和w频段

这篇文章有用吗?

平均时间和光谱的差距

相关的帖子