稳定局部湍流封闭模型
摘要边界层物理学的一个基本问题是将有限的测量结果外推到平均速度和标量性质的一般描述,以及它们在直接边界处的雷诺数。对于大气表面层,广泛的研究致力于相对简单的通量测量方法。这种方法的核心是描述动量和标量变量的表面粗糙度。通常,塔台配备两级或两级以上的仪器,表面通量可以通过使用某种形式的莫宁-奥布霍夫无因次梯度(例如,Businger等,1971年;Andreas和Claffey 1995年),或由直接协方差或光谱技术确定的平均梯度和通量的组合(例如,Edson等人,1991年)。
在IOBL中,由于各种原因,这就不那么简单了。首先,与上层海冰表面相比,冰下形态的变化往往占整个边界层的很大一部分。如果IOBL的尺度约为大气边界层的1/30,那么1米帆和5-6米龙骨的压力脊对各自边界层的表现完全不同。总的来说,对于IOBL参数化问题,许多表面层假设(恒定应力、应力和平均速度共线无方向变化等)显然是不合适的。
如第八章所述,在给定初始条件下,有时可以求解一个随时间变化的数值PBL模型,让它随着强迫场的变化而变化。给定在特定位置观测的适当时间序列,只要模型能够再现观测到的特征(例如混合层温度、盐度、深度),该模型将对跨海底界线的总体交换提供合理准确的描述。这取决于具有现实的初始条件和合理准确的强迫场时间序列(例如,风或冰的速度,冰中的传导热流等)。在许多情况下,观测在时间和位置上都是分散的(例如,区域调查期间从船只或飞机上获得的站点),人们希望产生OBL结构的“快照”,以估计混合层表面或底部附近的通量。
M.麦克菲,空气-冰-海洋相互作用,173-192。©施普林格科学+商业传媒b.v., 2008
即使存在一个相对完整的测量集,我们也经常面临在几个位置进行测量的外推抽样问题(这是因为操作注意事项(通常偏向于相对光滑的冰)到对整个周围环境的一般描述冰原,这反过来可能适合于在数值模型中描述网格单元(这有时被称为“缩放”问题)。来自ISPOL (McPhee 2008,出版中)的一个例子可以澄清这个问题。我们在威德尔海西部向北漂去的浮冰是由几种不同类型的冰组成的混合体,其中包括厚脊状的部分,较薄的第一年冰区,以及相当光滑的大约2米厚的多年冰区。在项目的大部分时间里,湍流桅杆位于最后一种类型的冰下,附近的下表面相当光滑,但在距离现场前100米左右的地方有压力脊和浮冰边缘。在项目的漂移阶段接近尾声时(12月25日),浮冰破裂,迫使湍流桅杆重新安置,在项目的最后一周,湍流桅杆位于一个小压力脊附近的薄冰下。
在第一次部署过程中,我们一直观察到湍流桅杆6米跨度内湍流应力随深度的大幅增加(参见McPhee 2008的图9.10),我们将其解释为较深的传感器捕捉到一些距离外的大型地下特征产生的湍流。在其他项目中也经常观察到这种现象,通常桅杆位于光滑的冰层下,但在一段距离内存在粗糙度特征,该距离大致由平均速度与尺度速度(u/u*)乘以从界面测量的湍流传感器深度所给出(Morison和McPhee 2001)。因此,例如,低于边界2米的TIC可能感知到大约30米内的粗糙度特征,而低于4米的湍流可能对100米外的地表下突出物做出响应。这个经验法则似乎适用于示巴和ISPOL (McPhee 2002)。
在项目结束时的短期部署中,最初分别在冰下1米和3米的地方放置了一个带有两个集群的桅杆,这样主要的潮汐流将从北方或南方穿过相对光滑的冰,并与位于西方的一个小压力脊平行。然而,在部署后不久,浮冰就会旋转,因此如果桅杆感应到的电流来自东北方向,龙骨就会直接位于湍流桅杆的上游,对上游几米的流动产生很大影响。该装置包括一个声学多普勒剖面仪,可提供大约10至30米深度的高分辨率电流剖面。第二个安装的两个例子如图9.1所示:一个是气流穿过光滑的冰面接近桅杆,另一个是相对气流几乎直接穿过压力脊龙骨。在前一种情况下,目前的结构表现出相当良好的发展埃克曼螺旋, 1 m处的摩擦速度约为5mm s_1,从直接应用LOW到无量纲速度,我们推断出表面粗糙度约为0.8 mm。当水流从龙骨处靠近时,来自ADP数据的10 - 30米范围内的蹄速图再次显示出预期的埃克曼转向,但此时TIC深度的水流只是较深水流的一小部分,表明水流堵塞。如果你*估计从
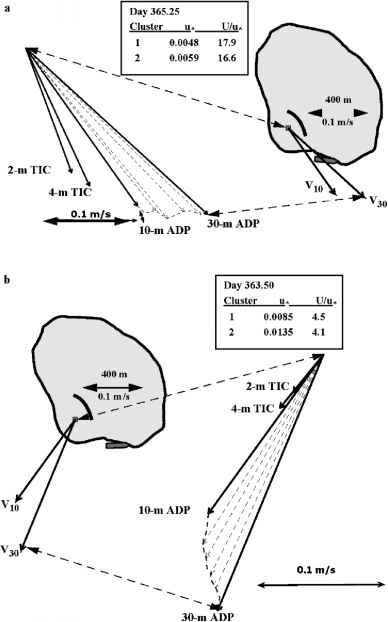
图9.1在ISPOL进行第二次部署时,相对于漂移浮冰测量的电流。图中显示浮冰轮廓和方向,桅杆位置用方形符号表示,水深10 m和30 m处的ADP电流矢量表示。北方向上。一个更完整的电流hodograph与TIC电流显示在放大视图。方框列出了摩擦速度和无因次电流。黑色的粗曲线代表了一个小压力脊的位置。a为3小时平均值,中心时间为365.25(2004年1月31日),气流从光滑的冰面靠近;b为时间363.5,气流从脊龙骨穿过
图9.1在ISPOL进行第二次部署时,相对于漂移浮冰测量的电流。图中显示浮冰轮廓和方向,桅杆位置用方形符号表示,水深10 m和30 m处的ADP电流矢量表示。北方向上。一个更完整的电流hodograph与TIC电流显示在放大视图。方框列出了摩擦速度和无因次电流。黑色的粗曲线代表了一个小压力脊的位置。以时间365.25(2004年1月31日)为中心的3小时平均值,水流从光滑的冰面接近;以时间363.5为中心的b,水流从山脊龙骨处1米处的协方差统计数据为表面值,Z0约为17厘米。由于来自压力脊的流动干扰如此之大,在通量测定基础上的许多假设都是可疑的,我们通常会将这些数据标记为不可靠的。另一方面,算例表明,压力脊龙骨上的形式阻力将构成浮体与海洋之间总动量传递的重要部分,除非下表面异常光滑。
评估一个压力脊龙骨的阻力和增强混合是一项艰巨的任务,需要大量的计算(参见Skyllingstad et al. 2003),并且将结果外推到整个非均匀浮冰增加了相当大的难度。然而,图9.1中较深的电流剖面暗示,通过考虑IOBL外部发生的情况,可以推断出代表整个浮体的表面特性,主要观点是,由于浮体作为刚体移动,在深度大于大多数地表下突出物的深度,湍流必须感知到一些综合影响的变化的表面条件。在本章中,我们将用一种基于ISPOL测量的建模技术来探索这一概念(McPhee 2008,出版中)。
9.1型号说明
与标量守恒方程不同,动量的埃克曼方程承认一个稳态解。局部湍流封闭模型(SLTC)的“稳定”版本被开发出来,作为在特定时间外推有限测量的手段,以推断整个边界层的结构。SLTC模型的主要假设和简化是湍流在表面条件下即时调整,因此守恒方程中局部时间相关项相对于垂直交换项可以忽略不计(例如,对于动量\ut \ ^ \tz - if u\),并且TKE的垂直输移在大多数IOBL实例中不是一个主要因素。虽然当存在较大的惯性振荡或在表面通量条件快速变化时,这些假设是可疑的,但它们通常会持续相当长的时间,特别是当冰盖很致密时。在实践中,这个模型需要对上层海洋的温度和盐度结构有一个合理的描述,还需要某种方法来估计界面处的摩擦速度,可能是根据冰的速度或表面风(如果冰是自由漂移的)。正如下面所解释的,该模型利用了一个迭代方案,首先估计IOBL涡流粘度仅从表面通量条件。然后通过雷诺数类比,利用涡流扩散系数对模型的涡流黏度进行估计。一般来说,这些通量会影响湍流尺度和涡旋黏度,因此用新的涡旋黏度重新求解稳态动量,重新计算通量等。我们证明(McPhee 1999),使用该模型模拟上层海洋温度和盐度的时间演变,产生的结果与使用秒矩封闭模型模拟的结果相似(Mellor和Yamada 1982年的21/2级)。后者需要对6个守恒方程进行前步,而SLTC时间只对T和S场进行步进。就计算成本而言,这种方法并没有太大的优势,因为迭代方案的计算成本很高,但重点是要表明,纯局部(在空间和时间上)湍流描述产生的通量与更复杂的模型相似,后者包含动量、TKE和主长度尺度的附加方程。
该模型采用的物理原理与第7章中描述的随时间变化的模型基本相同,不同之处是,该模型考虑的是一个固定的上层海洋温度和盐度状态,具有一组界面通量条件,并根据涡旋粘度和标量扩散率的物理合理分布迭代得到动量和标量通量的解,而不是受规定的表面条件所迫从初始状态向前推进。
9.2涡流粘度/扩散系数迭代
不像依赖时间的模型,对于每一个时间步浮力通量“独立”SLTC模型从浮力通量的初始猜测开始,然后迭代到一个解,其中建模的u*和观测到的T/S廓线确定边界层结构。
为了说明该方法,考虑SHEBA项目后期的3小时潜在温度和盐度平均剖面(图9.2),并假设u*o = 18mms_1是规定的。这与海洋上部的T和S一起用于计算(w' b%。涡流粘度的初始猜测(图9.3a)是通过确定最大值Kmax = u*oAmax来实现的,其中Amax是根据第7.6节中描述的算法从u*o和w' b'} o确定的。假定应力呈指数衰减,但在表面层,应力随K |z| u*o变化。这一估计值假设整个水柱的中性稳定性,因此标量扩散系数等于粘度,粘度远远超过了混合层深度(由图9.2b中的虚线表示),仍然是不切实际的大。正如从a到b的箭头所示,将标量扩散系数应用于观测到的0和S剖面,可以对整个OBL的浮力通量进行初步估计,在混合层以下,浮力通量也大得不切实际。通过应用混合长度算法对(w' b'}(图9.3b)和u*o沿指定的界面通量进行轮廓的第一个模型估计,然后进行第二次Km估计(图9.3c),从中进行新的估计(图9.3 3d),以此类推,对指定的迭代次数进行估计。下一次迭代后的涡流黏度和浮力通量结果如图9.3e和f所示,以及10次迭代后的结果(灰色曲线)。
图9.4显示了模拟涡流粘度的细节,以及两个tic对涡流粘度的估计,由局部摩擦速度和混合长度的乘积计算得出(与处的波数成反比)
潜在温度
潜在温度
-
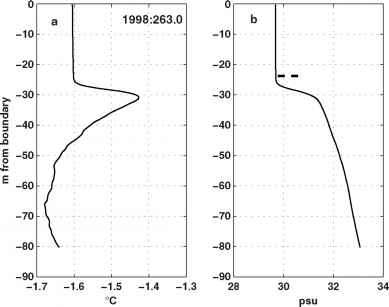
- 图9.2 1998年9月20日00:00UT为中心的示巴廓线3小时平均位温和盐度,用于说明SLTC模型。虚线表示混合层中的最后一个网格点
w谱中的最大值)。在跃层的上部(图9.4b), Km随着距跃层深度的距离呈指数下降,跃层深度定义为浮力频率平方首次超过最小值的水平,在这种情况下为2.5 x 10-5 s-2。u*p和(W b’)p在跃层水平上的模型解的组合决定了上跃层中的X。在斜跃层的稳定分层中,标量扩散系数与涡流粘度的比值是梯度理查德森数的函数(第7.6节),因为湍流比标量性质更有效地传递动量。这导致了Kh随深度的快速下降。
由Km和数值速度梯度的乘积得到的建模雷诺应力,如图9.5a所示为u*(运动应力大小的平方根)以及测量值。在这个演示中,选择u*0,使模拟应力与在较低的仪器组(冰下6米)测量的应力相匹配,通过对初始猜测进行连续调整,假设从界面到6米水平呈指数下降。图9.5b所示的模拟热通量(-pCpKhQz)表明,在良好混合层的上部,向上的通量大约为10 W m-2,与仪器集群水平上的测量结果(pCp (W T’))一致。请注意,热通量剖面的唯一“建模”部分是涡流扩散率Kh。计算结果与界面通量随混合层温度升高(方号)的变化一致。在下半部分
9.2涡粘度/扩散系数迭代涡粘度
一个 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||














