Ck T7 Tytk yy y m i

其中N是样本容量，k是时间滞后。rk与k的关系图，即相关图，可以给出潜在时间序列的持续程度的概念，它可能有助于选择可能代表该序列的随机模型的类型。当相关图在几次延迟后迅速衰减为零时，这可能表明序列中的持久性较小或内存较短，而相关图的缓慢衰减则表明持久性较大或内存较长。滞后一序列相关系数r]是一个简单的度量序列的时间依赖程度。一般来说，年流量的r]很小，但为正，尽管由于样本的可变性，可能会出现负r]。年流量rx值大的原因有很多，包括自然或人工地表蓄水的影响，如湖泊、水库或冰川，地下水蓄水响应缓慢的影响，以及非平稳性的影响。估计量s2, g和rk是有偏差的(相对于相应的总体统计数据向下)。已建议对这些估计量的偏差进行修正(Bobee和Robitaille, 1975;Yevjevich, 1972;Fernandez和Salas, 1990)。

此外，样本谱是研究水气候系列在频域变异的另一种方式(Yevjevich, 1972b)。样本谱g(fj)可确定为gifj) = 2

其中Dk是平滑函数，m是考虑的最大滞后数。图4显示了1900-1999年期间年度PDO指数时间序列的自相关函数和频谱。时间序列显示低频成分的证据，这些低频成分表现为缓慢衰减和伪周期相关图，以及在每年0.02和0.18个周期附近频率具有可见高值的频谱。

在联合分析几个时间序列时，交叉相关性可能很重要。序列y®- a "<7) i与j之间的相互相关系数确定为和_y，， t - 1，…， N表示车站

r'Jk和k的关系图是交叉相关图。对于n个时间序列，r\， i =…，n和j = 1，…，n是滞后-k互相关n x n矩阵Mk的元素。图5是为科罗拉多河系统29个站点的年流量获得的滞后-零相互关矩阵的图形显示。作为参考，1号站是上游最远的站点之一，29号站是下游最远的站点之一。站1与29之间的相互关系较大(约为0.9)，而站1与27之间的相互关系较小(约为0.9)

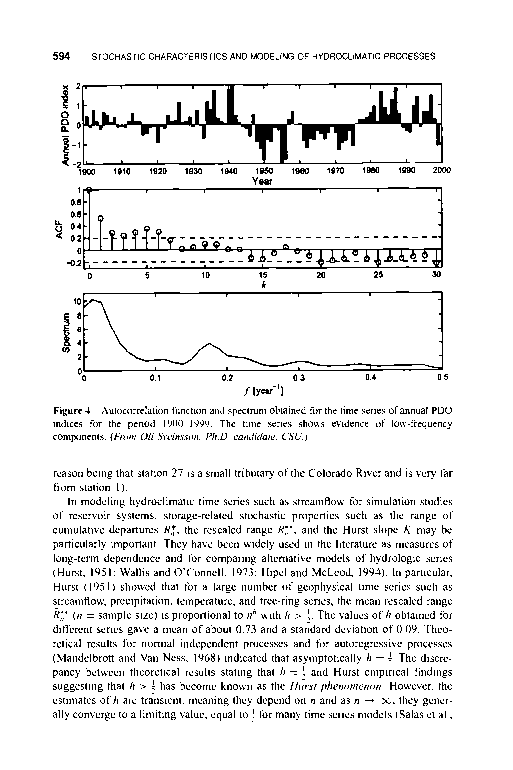
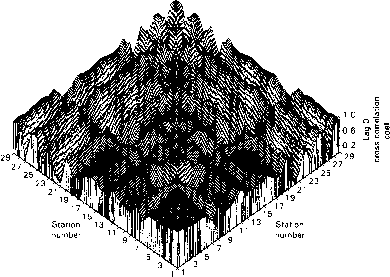
图5科罗拉多河系统29个站点年流量的滞后零互相关矩阵。作为参考，站1是最远的上游站点，站29是最远的下游站点。

1979)。赫斯特现象的一种解释是将h - j与具有短期依赖结构的短记忆模型联系起来，将h > \与具有长期依赖结构的长记忆模型联系起来。包括自回归移动平均(ARMA)过程在内的许多模型可以具有长期依赖结构，但渐近地它们给出h = i。此外，具有长期依赖且h > \的平稳模型是分数阶ARMA (FARMA)模型(请参阅第4节ARMA和FARMA过程的定义)。h的估计可用于比较替代建模策略和估计程序的性能。也可用统计检验来确定给定时间序列是否表现出赫斯特效应(Mesa和Poveda, 1993年)。

此外，与干旱相关的随机特性在降水和径流等水文气候时间序列的模拟中也很重要。考虑一个水文时间序列yt, t - 1n和一个需求水平d(交叉水平)。

假设y是一个年度序列，d是一个常数(例如，d = ay, 0 < a < 1)。当y < d时，在任何给定时间t发生亏缺。连续的亏缺序列(直到y， > d)可以称为干旱，这种干旱可以用其持续时间L、大小M和强度/ = M/L来表征(Yevjevich, 1967)。由于在给定的水文样本中可能发生若干次干旱，因此(在给定的样本中)最大干旱持续时间、幅度和强度已成为所谓临界干旱的指标，并已广泛应用于水资源研究。

周期性(季节性)统计特性

虽然上述定义的水文气候时间序列的总体随机特性可以从年度序列或整个季节序列中确定，但特定的季节(周期性)特性可以更好地描述某些时间间隔小于一年的水文气候时间序列的随机特性，如月流量数据。设季节时间序列用yv v = 1表示，…/ V;1，…，其中v为年份，r为季节，N为记录的年数，co为每年的季节数(例如，每月数据为to = 12)。然后，对于每个季节r，可以确定一些统计数据，如季节平均值y%，方差si，变异系数cvT和偏态系数gz。此外，季节间相关系数rk z可由

例如，对于每月的流量，r14表示第四个月的流量与第三个月的流量之间的相关性。同样地，对于多个季节时间序列，季节性时间序列vi'l和y\'\之间的滞后-/:季节相互相关系数r\ T。K代表I和j，可以确定。

统计数据yt, sz, gz和rk T可以与时间r = 1，…，以观察它们是否有季节性变化。用傅里叶级数拟合这些统计数据对于每周和每天的数据尤其有效(Salas等，1980)。一般来说，对于季节性水流系列yt > sT，虽然对于某些溪流yx可能小于s%，特别是在“低流量”季节。此外，对于间歇性水流序列，其平均值一般小于标准偏差，即全年yx < sT。同样，旱季偏态系数gT的值一般比湿季偏态系数gT的值大，表明旱季数据比湿季数据更偏离正常。间歇水文序列的偏度值通常大于类似非间歇水文序列的偏度值。枯季河流流量的季节相关性rk z一般大于雨季的季节性相关性，并且在大多数月份中它们显著地不同于零。图6显示了科罗拉多河系统29个站每月流量的r, T，即滞后-1个月与月的相关性。可以观察到，相关性随月份而变化，除了少数例外，整个系统的相关性模式是相似的。另一方面，月降水量的季节相关性一般较低，或在大多数月份中与零没有显著差异(Roesner和

Ck,T = T;U(j;v,T -yz)(yv,z-k -yz-k)

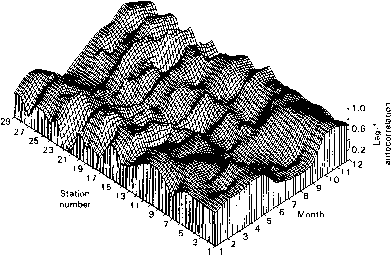
图6科罗拉多河系统29个站月流量的滞后-1月相关性，即rl T。

Yevjevich, 1966)，而对于周、日和小时降水，它们通常显著且大于零。

当相关性rk/I显著时，季节性流量的复杂长期依赖性(长记忆)可能是明显的，并且随着k的增加而缓慢衰减，超过季节(超过一年)。对于许多河流来说，这些相关性通常很小或不显著，但在尼罗河等河流系统中，这种季节性相关性可能会持续数年。在季节流量上表现出长期相关性的河流，在年流量上也会表现出长期自相关性。此外，一些河流水文图，如日和周水文图，可能具有方向性(不可逆性)，这意味着当时间方向相反时，它们的一些统计性质会发生变化。从上升段比下降段短的典型水文图中可以明显看出这一点。在这种情况下，数学模型具有方向性属性是可取的(Fernandez and Salas, 1986)。

随机模型和建模技术

为了模拟和预测水文气候过程，已经开发了许多随机模型和建模方案。有些模型是以概念(物理)为基础的，有些是经验的，或者是从其他领域开发的现有模型转换或改编而来的，而另一些则是专门针对所审议过程的某些特定特征而产生的。

一般来说，连续时间过程的模型和短时间尺度(如小时)的模型比大时间尺度的模型更复杂。此外，有些模型是专门为降水而开发的，而另一些则是为水流而开发的。然而，它们中的许多对这两个过程和许多其他水气候过程都是有用的。在此，我们将举例说明自回归和移动平均(ARMA)模型以及它的扩展和修改。这些模式在许多水文气候过程的模拟和预测中都很受欢迎。然而，已经开发了许多其他随机模型，其中一些与ARMA模型有很大不同，它们针对的是所考虑的特定过程或人们试图解决的(潜在过程的)特定特征。例如，对于日降雨量等间歇过程，马尔可夫链和ARMA模型的离散对应物，即离散ARMA (DARMA)是可用的(例如，Chang et al.， 1984;Guttorp, 1995)。同样，具有无限内存的模型，如分数高斯噪声(例如，Mandelbrot和Van Ness, 1968)和能够模拟突然移位的移动水平模型(例如，Salas和Boes, 1980)是可用的。

随机模型

固定的模型。ARMA模型系列已广泛用于模拟不同时间尺度的水文气候过程。ARMA(p, q)模型定义为(Brockwell and Davis, 1991)

p iyt = j" + E fyyt -j - n) +£t - E 9j£H (5a)

4>(B){yt ~H)= 9(B)et (5b)

其中(i, 0，和

4>(B)= 1-pBp (6a)

0(B) = 1 - 0,5' - B2B2-----eqBq (6b)

由(5)导出的特定模型是ARMA(p, 0)或AR(p)和

ARMA(0, q)或MA(q)模型。此外，将分数阶自回归移动平均FARMA(p, d, q)模型定义为(Hosking, 1981;蒙塔纳里等人，1997)

(j)(B)(\ -B)d(yt-fi) = d(B)et - 0.5 < d < 0.5 (7)

该模型能够表示长期依赖。上述ARMA和FARMA模型是平稳的，因此，将其应用于水文气候时间序列建模需要底层数据是平稳的，或者通过适当的转换将其转换为平稳的。

这些模型已普遍应用于年水文气候资料。有时它们在季节标准化后被应用于季节数据。同样，它们也被应用于季节标准化后的每日数据，或者将一年分为几个季节，并对每个季节的每日序列应用不同的模型。例如，parrange等人(1992)将基于物理的概念应用于土壤湿度的日常变化，并发现它可以用AR(1)过程来描述。AR和ARMA模型的性质，如自相关函数、方差和谱，以及水文应用可以在Salas等人(1980)、Loucks等人(1981)、Bras和Rodriguez-Iturbe(1985)、Salas(1993)和Hipel和McLeod(1994)中找到。Chu和Katz(1985)还将AR和ARMA模型与季节性和月度南方涛动指数(SOI)进行了拟合。在拟合模型之前，从数据中去掉了年周期，以使其稳定。Xu和Storch(1990)使用主振荡模式(POP)分析对月度SOI数据进行建模。他们的结论是，他们的POP方案优于ARMA方案。此外，Chu等人(1995)应用双变量AR模型对佛罗里达州的季节性SOI和降水指数进行联合建模。 The fitted bivariate AR model was then used to forecast precipitation.

周期模型。文献中提出了一些周期和其他非平稳模型，如PARMA系列、ARIMA和乘法PARMA模型，用于模拟季节性水文气候过程，如季节性降水和水流系列(Salas等，1980;劳克斯等人，1981;萨拉斯,1993;Hipel和McLeod, 1994)。特别地，PARMA(p，#)模型定义为且B'zv_T = zv T_，。当q = 0时，上述模型就变成了众所周知的PARMA(/j, 0)或PAR(//)。更具体地说，PAR(l)模型(也称为Thomas-Fiering模型)可能是水文学中使用最广泛的模型之一。一般来说，低阶PARMA模型已成为模拟季节水文气候过程的流行模型。基于物理的或概念性的流域或流域的潜在水文循环论证证明了这些模型的适用性。 For instance, Salas and Obeysekera (1992) showed that assuming that the precipitation input is an uncorrected periodic-stochastic process and under some p 1

在哪里

x{B) = 1 - cj>uBl -4> 2 xB2-----4>PiXBP

0 t (5) = 1-01 i5 -02, t52——O ^ Bfl

考虑了线性水库对地下水储量的考虑，季节性水流的随机模型就变成了PARMA(1,1)过程。Chu et al.(1995)分析了季节性和月度SOI的时间序列，并在数据中去除年度周期后拟合了AR和ARMA模型。他们还使用了季节性系数变化的ARMA模型。

此外，ARIMA(jt?， d, q)、乘法ARMA和乘法ARIMA模型已被应用于预测水文气候过程(例如，Salas等，1980;Hipel和McLeod, 1994)，地下水水位采样(Ahn和Salas, 1997)，以及气候时间序列趋势的探测和估计(例如，Visser和Molenaar, 1995;Zheng and Basher, 1999)。此外，对复杂过程(如尼罗河月流量)的模拟已经用乘法PARMA模型完成(Salas et al.， 1995)。此外，Lund等人(1995)提供了具有周期相关结构的气候时间序列的分析和建模的总体概述。他们提出了一种检测周期相关性的检验方法，并应用PARMA模型对这些序列进行建模。虽然所提到的平稳和非平稳模型[分别为模型(5)和(8)]是为单点或单变量系列编写的，但它们的多点或多变量对应物也是可用的(例如Salas, 1993;Hipel和McLeod, 1994)。

预测的随机模型

许多随机模式已被广泛应用于降水和径流等水文气候过程的预测。许多这样的模型属于传递函数模型家族。一般的传递函数噪声(GTFN)模型可以写成y(B)(y，

其中}'(B)， oj(B)， <5(B)， 0(B)， 0(B)为B中不同阶数的多项式[类似于式(6)中定义的多项式]，xt为降水或ENSO指数等外生变量，yu's表示均值，r为时延，e为噪声项。一些特殊情况(型号)，如ARMA, ARMAX，单位自记水位计类型、多元线性回归和Box-Jenkins传递函数噪声模型可以从(10)中推导或简化。式(10)假设单点变量，但如果变量为向量，参数为矩阵，则适用于多点变量。许多这些模型的应用可以在Hipel和McLeod(1994)中找到。此外，基于ARMA、ARMAX和GTFN模型的预测方程可以写成顺序和递归形式(例如，使用卡尔曼滤波器)。此外，人工神经网络(ANN)在过去十年中已经出现，作为许多建模应用的有用技术，包括预测(例如，Hsu等人，1995;Govindaraju和Rao, 2000)。这些模型的应用很多，估计程序，以及人工神经网络算法预测降水在Valdes et al.(2001)中有一些详细的描述。

建模方案

在水文领域已经发展了一些具体的模型，以解决与水文和水资源问题有关的一些独特特征。一个例子是所谓的分解模型(例如，Valencia和Schaake, 1973)。一些传统模型(如PAR(l)模型)无法重现年度统计数据(或高档统计数据)，导致了分解技术的发展。虽然这种分解模型的主要目的是使人们能够生成水文序列，从而再现年度和季节时间尺度上的统计数据，但它也为复杂水文过程和复杂水文系统的建模能力带来了一个主要方面。复杂系统涉及多个地点，时间和空间质量平衡的要求，往往需要使用建模方案，可能包括单地点，多地点，和时间和空间分解模型的阵列。虽然这一要求在为模拟而构建的模型中更为明显，但对于预测复杂的水文系统也是如此。此外，为了促进随机模型在水文过程模拟中的实际应用，开发了SPIGOT (Grygier and Stedinger, 1990)和SAMS (Salas et al.， 2000)等软件包。然而，在现实世界系统中，特别是模拟复杂的水文过程和复杂的水资源系统，如北美的五大湖系统或非洲的尼罗河系统，这些软件包的实际应用可能不是一个简单的应用。因此，在获得令人满意或可接受的问题解决方案之前，可能必须进行调整、修改、添加等。

随机建模

水文气候过程的随机建模包括四个主要步骤:模型识别、参数估计、模型检验和模型验证。模型识别是指确定特定的模型结构和模型顺序;例如，确定年流序列的模型是ARMA(1,1)或确定日降雨量的模型是一个简单的马尔可夫链。一般来说，属于ARMA、ARIMA和传递函数模型家族的模型适用于基于自相关、偏相关和互相关分析的某些识别程序(Brockwell和Davis, 1991;Hipel和McLeod, 1994)。但是，有些模式无法进行模式识别或模式过于复杂，因此将某一类型和顺序的模式应用于手头的特定水文气候系列，并通过测试和验证来判断其性能。一些水文气候过程，如水流和土壤湿度，已经使用基于物理的概念和论据来确定(例如，Salas和Smith, 1981;帕兰吉等人，1992年;Salas和obbeysekera, 1992)。

一旦确定了模型，就可以根据特定的模型和手头的数据，通过一些技术来估计其参数，如矩量法、最小二乘法和最大似然法。矩估计程序的典型方法包括匹配历史和总体(模型)一阶和二阶统计量，尽管在某些情况下使用了一些其他性质，如偏度和存储和干旱相关的统计量(例如，Salas等人，1980年;Hipel和McLeod, 1994)。此外，递归参数估计方法和过滤技术特别用于预测问题(例如，Bras和Rodriguez-Iturbe, 1985年)。此外，无论是模拟还是预测，对水文气候时间序列的建模通常要求将基础序列转换为近似正态分布序列(例如，Salas, 1993;Hipel和McLeod, 1994)。因此，参数估计通常在变换域内进行。对于ARMA、ARIMA、ARMAX和传递函数类型的模型，已经很好地开发了模型测试程序(例如，Brockwell和Davis, 1991)。同样，PARMA模型的测试程序也可用(例如，Salas等人，1980;萨拉斯,1993; Hipel and McLeod, 1994). The tests usually involve diagnostic checks to verify whether the model residuals comply with the underlying assumptions of independence and normality (of the residuals). Since many models may comply with such requirements, a model selection criteria based on the Akaike Information Criteria (AIC) is available to discriminate and find a parsimonious model (Brockwell and Davis, 1991). On the other hand, model testing for some other models cannot be done based on analysis of residuals; so instead model testing is based on data generation experiments. In addition, model verification is usually needed beyond testing residuals depending on whether the modeling exercise is geared to simulation or forecasting. For instance, for simulation (data generation) one may like to test whether the model is capable of generating sequences that reproduce a number of storage and drought related historical characteristics. This is usually accomplished by Monte Carlo experiments. On the other hand, model verification for forecasting may involve examining whether the model is capable of estimating the水文过程在指定的错误标准内，提前考虑一个或多个交货时间。这可以通过分割抽样估计和测试来实现。

参考文献

安，H.，和J. D.萨拉斯，基于随机分析的地下水头取样，水

Resour。第55(12)号决议，2769-2780,1997。Bobee, B.， R. Robitaille，偏度系数估计中的偏差修正，

水Resour。第11(6)，851-854,1975。Bras, R. L.和Rodriguez-Iturbe，随机函数和水文学，Addison-Wesley, Reading, MA, 1985。

布罗克韦尔，P. J.和R. A.戴维斯，时间序列:理论与方法，第二版，斯普林格出版社，纽约，1991年。

张，t.j.， M. L. Kawas和J. W. Delleur，每日降水离散自回归移动平均过程建模，水资源。第20(5)，565-580,1984。朱，P. S.，和R. W. Katz，南方涛动的建模和预测:一个时域方法，月天气预报，113,1876-1888,1985。

朱培生，R. W. Katz，丁培平，佛罗里达季节降水的建模和预测:一个矢量时域方法，Int。j . Climatol。， 15, 53-64, 1995。

伊士曼，J. L.， M. B. Coughenour, R. a . Pielke，用植物和气象耦合模型研究二氧化碳和景观变化的影响，全球变化生物学。， 1,797 -815, 2001。

经济学家，《灾难》，2001年3月31日，106期。

李文杰，杨晓明，苏丹中部地区年降水量的反馈机制研究。， 110, 323-334, 1989。

埃尔塔希尔，E. A. B.厄尔尼诺现象和尼罗河流动的自然变化，水资源。第32(1)，131-137,1996。

费尔南德斯，B.和J. D.萨拉斯，运行水文的周期性伽马自回归过程，水资源。第22(10)号，第1385-1396号，1986。

费尔南德斯，B.和J. D.萨拉斯，伽马-自回归模型的流模拟，J. Hydrol。Eng。中国科学院学报(自然科学版)，29(4)，344 - 344,1990。

Govindaraju, R.和a.r. Rao(编者)，水文中的人工神经网络，Kluwer学术，伦敦，2000。

Grygier, J. C.和J. R. Stedinger, SPIGOT，合成流生成软件包，技术描述，2.5版，康奈尔大学，土木与环境工程学院，伊萨卡，纽约，1990。

古托普，P.，科学数据的随机建模，查普曼和霍尔，伦敦，1995。

Helsel, D. R.和R. M. Hirsch，水资源的统计方法，环境科学研究49,Elsevier，阿姆斯特丹，1992。

李志伟，杨晓明，《水资源与环境系统的时间序列模型研究》，中国科学技术研究院，1994。

胡士金，分数差分，生物计量学，68,165-176,1981。

徐k, H. V . Gupta, S. Sorooshian，降雨径流过程的人工神经网络建模，水资源。决议，37(10)，2517- 2530,1995。

张志强，水库长期存贮能力研究，中华人民大学学报。阿斯，116,770-799,1951。

Kalnay, E.， M. Kanamitsu, R. Kistler, W. Collins, D. Deaven, L. Gandin, M. Iredell, S. Saha, G. White, J. wooollen, Y. Zhu, M. Chelliah, W. Ebisuzaki, W. Higgins, J. Janowiak, K. C. Mo, C. Ropelewski, J. Wang, A. Leetmaa, R. Reynolds, R. Jenne和D. Joseph, NCEP/NCAR 40年再分析项目，Bull。点。Meteorol。Soc。， 77,437 -471, 1996。

卡茨，R. W.和M. B.帕兰吉，链相关过程的推广:应用于小时沉淀、水Resour。第37(5)号决议，1331- 1341,1995。

Kerr, R. a .揭露变化无常的气候系统，研究新闻，25raybet雷竞技最新5,1508 - 1510,1992。

Landsea, c.w.， W. M. Gray, P. W. Mielke Jr.， K. J. Berry和R. K. Taft，北非6月至9月的降雨:1999年的季节预报，科罗拉多州立大学大气科学系，柯林斯堡，CO .，在线可得，http://typhoon.atmos.colostate.edu/forecasts/1999/sahel_jun99/, 1999年。

劳克斯，D. P.， J. R. Stedinger，和D. Haith，水资源系统规划与分析，Prentice-Hall, Englewood Cliffs，新泽西州，1981。

李志刚，刘志刚，刘志刚，刘志刚，基于时间序列的气候变化研究，气候科学进展，28(1):1 - 7,1995。raybet雷竞技最新

曼德布罗特，B. B.和J. W. Van Ness，分数阶布朗运动，分数阶噪声及其应用，科学通报，70(4)，422-437,1968。

台面,0。杨晓明，《赫斯特效应:波动尺度法》，水资源。中华人民共和国宪法，29(12)，3995^002,1993。

Montanari, A.， R. Rosso，和M. S. Taqqu，应用于水文时间序列的分数差ARIMA模型:识别、估计和模拟，水资源。第33(5)号决议，1997。

李国强，李国强，张志刚，时间降雨模型的参数估计，水资源研究。Res. 23(10)， 1837-1850, 1987。

帕兰奇，M. B.， G. G. Katul, R. H.昆卡，M. L. Kavas, D. R. Nielsen, M. Mata，土壤含水量时间序列模型的物理基础，水资源。第28(9)号决议，第2437-2446号，1992年。

陈志伟，陈志伟，陈志伟，水资源脆弱性评价，环境科学，39(2)，1999。

Roesner, L. A.和V . Yevjevich，月降水和月降水时间序列的数学模型径流，在水文学论文，第15期，科罗拉多州立大学，科林斯堡，科罗拉多州，1966年。

萨拉斯，《水文时间序列的分析与建模》，载《水文手册》(编)，纽约，1993，第19章。

萨拉斯，J. D.和D. C.博斯，水文系列的移动水平模型，水资源。， 3, 59-63, 1980。

萨拉斯，J. D.和J. T. B.欧贝塞克拉，季节流时间序列模型的概念基础，ASCE J.水力。Eng。岩石力学与工程学报，18(9)，1186-1194,1992。

萨拉斯，J. D.和R. A.史密斯，年流量随机模型的物理基础，水资源。决议，17,428^* 30,1981。

王志刚，王志刚，王志刚，王志刚，赫斯特现象的预渐近行为，中国机械工程，44(1)，1-15,1979。

Salas, J. D.， J. R. Delleur, V . Yevjevich, W. L. Lane，水文时间序列应用建模，水资源出版物，Littleton, CO, 1980。

萨拉斯，J. D.， N.萨达，和C. H.钟，尼罗河系统月流量的随机建模和模拟，科罗拉多州立大学，工程研究中心，水利工程。实验室。，技术报告第5号，Fort Collins, CO .， 1995。

萨拉斯，J. D.， N. Saada, C. H. Chung, W. L. Lane，和D. K. Frevert，随机分析，建模和仿真(SAMS)， 2000版，用户手册，科罗拉多州立大学，工程研究中心，液压。实验室。，技术报告第10号，Fort Collins, CO, 2000。

Salas, J. D.， J. A. Ramirez, P. Burlando，和R. Pielke, Sr.，降水和流过程的随机模拟，T. D. Potter和B. Colman(编)，天气、气候和水手册，第33章，John Wiley & Sons, Inc.，纽约，2002。raybet雷竞技最新

Sarewitz, D.， R. A. Pielke, Jr.和R. Byerly(编)，《预测:科学决策和自然的未来》，岛出版社，Covelo, CA, 2000。

快速的气候变化，美国。raybet雷竞技最新科学。， 87, 320-326, 1999。

巴尔德斯，j·B·p·布兰多和j·d·萨拉斯，随机预测降水和水流过程，见T. D. Potter和B. Colman(编)，《天气、气候和水手册》，第34章，John Wiley & Sons, Inc.，纽约，2002。raybet雷竞技最新

巴伦西亚，R. D.和J. C. Schaake, Jr.，分解过程随机水文，水资源。第1(1)号，1973。

维瑟，H.和J. Molenaar，气候时间序列的趋势估计和回归分析:结构时间序列模型和卡尔曼滤波器的应用，气候，8,969 -979,1995。raybet雷竞技最新

弗罗斯马蒂，c.j.， P.格林，J.索尔兹伯里和R. B.拉默斯，全球水资源:气候变化与人口增长的脆弱性，科学，28,raybet雷竞技最新284 - 288,2000。

沃利斯，J. R.和P. E.欧康奈尔，牢固的水库产量:水文记录的可靠性，水文科学。Bull(现为Hydro I. Sci。J.)， 18, 347-365, 1973。

徐建生，徐建生，用主振荡模式分析预测南方涛动，中国气象，27(3)，426 - 426,1990。raybet雷竞技最新

Yevjevich, V，大陆干旱的定义和调查的客观方法，《水文论文》第23卷，科罗拉多州立大学，Fort Collins, CO, 1967。

Yevjevich, V，水文时间序列的结构分析，《水文论文》第56卷，科罗拉多州立大学，柯林斯堡，CO, 1972a。

Yevjevich, V.，水文学中的随机过程，水资源出版物，利特尔顿，CO, 1972b。

郑晓峰，郑晓峰，郑晓峰，全球和区域时间序列的结构时间序列模型和趋势检测，气候变化研究，12(4)，1999。raybet雷竞技最新

继续阅读:降水和水流过程的随机模拟

这篇文章有用吗?

0 0