降水和水流过程的随机模拟
JOSÉ D.萨拉斯,JORGE A. RAMIREZ, PAOLO BURLANDO,老罗杰A. PIELKE。
降水和水流等水文气候过程的随机模拟已经成为分析许多与水有关问题的标准工具。模拟表示“模仿”底层流程的行为,以便对其进行真实的表示。为此目的,文献中提出并发展了许多基于经验的、基于数学/物理的、基于数学/随机的、基于模拟/物理的以及基于物理/实验室规模的模型和方法。本章强调基于随机和概率技术的模拟。此外,重点将放在降水和水流过程上,尽管本文所包括的许多方法和模型同样适用于其他水文气候过程,如évapotranspiration、土壤湿度、地表水和地下水水位以及海面温度。
随机模拟使人们能够获得未来可能发生的同等可能的水文气候过程序列。它们对许多水资源问题都很有用,例如(a)在不确定水流条件下估计水库系统的设计容量,(b)在不确定系统输入条件下评估水资源系统满足预计需水量的性能,(c)根据所考虑的供水系统关键点的模拟水流估计干旱性质,如干旱长度和强度。(d)推导a的底层输出变量的分布地下水流量方程(例如,水头),给定参数(例如,水力传导率)的分布和边界条件,(e)建立-
《天气、气候和水手册:大气化学、水文和社会raybet雷竞技最新影响》,托马斯·d·波特和布拉德利·r·科尔曼编辑。ISBN 0-471-21489-2©2003 John Wiley & Sons, Inc.
将多孔介质中污染物传播时间和传播的不确定性作为地下水污染传输模型参数不确定性的函数,并(f)分析大规模气候变率和全球气候变化对供水可用性和后续规划的影响raybet雷竞技最新水的运行资源项目。
连续时间降水的随机模拟
自Le Cam60提出泊松过程可以模拟阵雨的发生以来,点过程理论已被应用于模拟连续时间降水。假设时间间隔(0,t)内到达某一定点的风暴次数N(t)是随参数It (I =风暴到达率)的泊松分布。参考图1(a), n个风暴到达区间(0,t)在时间tx,…t”。任意时间区间T内的风暴数也是随参数kT呈泊松分布。进一步假设与风暴到来相关的降雨量R是白噪声(例如R可能是伽玛分布的),并且N(t)和R是独立的。因此,降雨量rx,…,rn对应发生时间tx,…,tn的风暴。这种降雨产生过程被称为泊松白噪声(PWN)。
(0,t)区间的累计降雨量,Z(t) = J^'i' Rj为复合泊松过程。连续非重叠时间间隔T的累计降雨量,即离散时间降雨过程(见图1),用Yl - Z(iT) - Z(iT - T)表示。i = 1,2,假设Z(T)由PWN模型生成,Yt的基本统计性质已被广泛研究。它的自相关函数pk(Y)对于所有大于零的滞后都等于零,这与实际观测值相矛盾[例如,根据1948-1983年的记录,丹佛机场站6月的小时降水px(Y) = 0.446]。尽管有这个缺点,但PWN模式对预测年降水和极端降水事件是有用的与其假设降雨在瞬间发生且持续时间为零,不如考虑降雨在持续时间D和强度I上是随机的,如图1b所示。这被称为泊松矩形脉冲(PRP)模型一个常见的假设是D和/是独立的,并且呈指数分布。图1 b显示了一个PRP过程,在(0,t)区间内n个风暴发生在时间t{,…,tn与相关的强度和持续时间
(/',, dx) (/ ", dn)。然后,风暴可能重叠和聚集过程Yt
成为autocorrelated。尽管PRP模型比PWN模型概念化得更好,但它在应用于降雨数据时仍有局限性因此,已经提出了基于集群概念的替代模型。
Neyman和Scott69在模拟星系的空间分布时最初提出了星系团的概念。Le Cam60, Kavvas和Delleur,51等人30'82'86"88将这种空间聚类概念应用于连续时间降雨模型。Neyman-Scott集群过程可以描述为一个两级机制
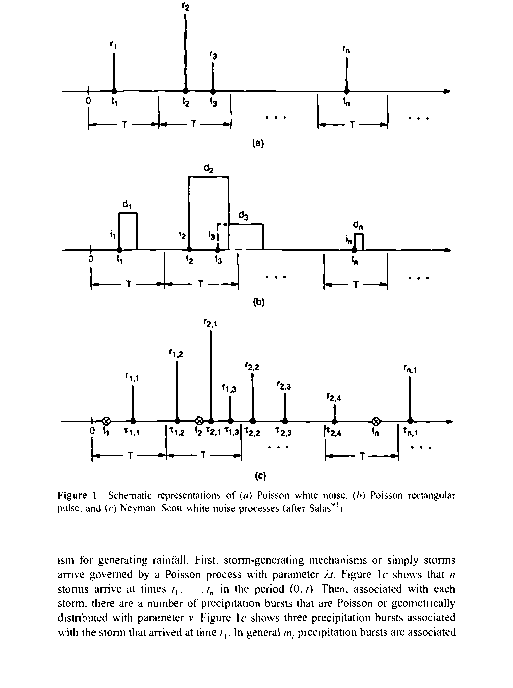
随着tj时间到来的暴风雨。此外,暴暴发生的时间t相对于暴暴起源i-可以假设为随参数ft呈指数分布(例如,在图lc中,第一个暴暴产生的三个暴暴分别位于相对于?,的时间t,,, t, 2和tl3)。然后,如果用瞬时随机降水深度R描述降水突发,则得到降水过程如果降水暴为矩形脉冲,则降水过程称为内曼-斯科特矩形脉冲。
Neyman-Scott (NS)模型的参数估计是近二十年来研究的一个重要课题。通常的估算是基于矩量法,尽管也提出了其他方法。一个明显的主要估计问题是基于数据估计的参数聚合级别(例如每小时)可能与从另一个聚合级别(例如每天)的数据估计的结果有显著不同。11'30'71'86问题似乎是,随着数据的汇总,信息丢失了,相应的二阶统计数据没有足够的信息来给出生成过程(模型)参数的可靠估计,因此,它们变得有很大的偏差。例如,Cadavid et al.11基于(已知)种群参数的NSWN模型进行了广泛的模拟研究:1 = 0.102 x 10_3/min, jS = 0.00221/min, fx = 24.36/in, l/v = 0.072(簇大小的几何分布参数)。使用小时和日序列来估计用于估计参数的矩(平均值、标准差以及滞后-1和滞后-2相关系数)。结果如表1所示。显然,尽管产生机制是已知的(NSWN),但当使用日数值时,获得的参数估计不太可靠。基于不同时间尺度的加权矩以最小二乘方式进行估计是一种替代方法。此外,物理因素可能有助于在某些参数中设置约束条件,根据统计因素初始化要确定的估计,以及将拟合的模型参数与一些已知的物理性质进行比较Koepsell和Valdes54利用Waymire等人提出的时空聚类模型应用这些概念来模拟德克萨斯州的降雨,并指出即使使用物理考虑因素也难以估计参数。
除了泊松过程和Neyman-Scott团簇过程外,还提出了基于Cox过程、103更新过程、7’31过程和bartlett - lewis过程的时间降水模型。40’87同样,另外的时空多维降水模型已经被开发出来(例如,Smith和Krajewski104)。此外,迄今提出的基于点和聚类过程的降水模型在某些方面存在局限性;例如,它们不包括在实际对流降雨过程中观测到的日周期性。49’71此外,Rodriguez-Iturbe等人提出了非线性动力学和混沌可能是某些水文气象过程(如降雨)的有用方法的问题。最后,对该领域的最新技术进行了出色的回顾32,并在一些杂志的特刊中汇编了一些与降雨分析、建模和可预测性有关的研究
参数(单位) |
人的价值 |
根据每小时数据估算” |
每日数据估计” |
À x 103 (1/min) |
0.102 |
0.103 |
0.091 |
ß x 103 (1/min) |
2.210 |
2.300 |
1.630 |
人工智能(信用证) |
24.360 |
23.990 |
7.010 |
1 / v |
0.072 |
0.072 |
0.247 |
“根据12个系列36,456码的时薪和12个系列1519码的日薪来估算。来自Cadavid等人。”
“根据12个系列36,456码的时薪和12个系列1519码的日薪来估算。来自Cadavid等人。”
期刊(如J.应用;流星。, 1993年第32卷;j .地球物理学。Res.第104卷,no。D24, 1999)。
小时、日、周降水
我们在前一节中已经看到,连续非重叠时间段的累积降水(即离散时间降水)的模型和性质可以从连续时间降水模型中推导出来。然而,人们可以直接在小时、日和周的时间尺度上制定降水模型。在这些情况下,马尔可夫链理论在文献中被广泛用于模拟降水(在离散时间),但许多其他水文进程S如水流、土壤湿度、温度、太阳辐射等
7 n 49 s-i是水库的储水。••••
假设X(t)是一个离散值过程,从时间0开始,随着时间发展,即i = 0,1,2,则P[X(t) = xt\X(0) = x0, X(\) =x1,…, X(t - 1) = X,_ j]是过程X(t) - xt给定其整个历史的概率。如果该概率化简为P[X(t) = X, | X(t - 1) = xt_,],则该过程为一阶马尔可夫链或简单马尔可夫链。由于X(t)是一个离散值过程,我们将使用X(t) = /', / = 1,…,r代替oiX(t) = x ",其中j表示状态,r是状态数;例如,在模拟日降雨量时,可以考虑r = 2, j =1表示旱天(无雨),j = 2表示雨天。一个简单的马尔可夫链由其转移概率矩阵P(t)定义,它是一个方阵,对于所有ij对,元素P ^t = P[X(t) - j\X(t - 1) = /]。此外,qj{t) = P[X(t) = /], / = 1,…, r为t时刻链处于任意状态j的边际概率分布,#-(0)为初始状态的分布。此外,如果P(t)不依赖于时间,马尔可夫链是齐次或平稳链,在这种情况下,使用符号P和py。对降水事件的模拟和预报有用的一些概率的估计是-阶跃转移概率p\j\给定分布qj(0)的边际分布qj(t),以及稳态概率向量q*。 These probabilities can be determined from well-known relations available in the literature.39'118
对简单马尔可夫链的估计相当于估计转移概率矩阵中p × j的元素。常用的估计方法有矩量法和最大似然法为了检验一个简单的马尔可夫链模型是否适合所考虑的过程,人们可以检查模型的一些假设,看看降水过程的一些相关性质是否再现(例如,将概率pff与从观测数据中获得的概率进行比较,此外,Akaike信息准则在选择马尔可夫链模型的阶数方面有帮助。15'48
虽然在某些情况下,简单的马尔可夫链可能足以表示降水的可变性,但通常可能需要更复杂的模型。例如,在对全年的日降雨过程进行建模时,马尔可夫链的参数可能随时间而变化(例如,对于双态马尔可夫链,转移概率p × j可能随时间而变化,可以用三角级数拟合估计以平滑样本变化90)。在其他情况下可能需要高阶马尔可夫链。Chin15分析每日降水美国大陆100多个气象站的记录,并得出结论,一般来说,二级和三级模式是冬季的首选一阶模型夏天比较好。此外,还提出了估计交替更新过程的傅立叶级数系数和日降雨量的马尔可夫链的最大似然方法90和小时降雨量的带有周期马尔可夫链的混合模型(以解释日周期性的影响)
月、季、年降水量
长时间尺度(如月)的降水建模通常比短时间尺度(如日)的降水建模简单,特别是因为长时间尺度的自相关性变小或可以忽略不计(低频情况除外21)。在这种情况下,对给定地点的降水建模相当于找出每个月的概率分布。通常每个月都需要不同的分配。另一方面,半干旱区和干旱区的季节降水数据可能在某些季节包含零值,因此降水是一个混合随机变量。设Xvx =第v年和第z季的降水量,定义PT(0) = P(XV r = 0), z=l,…,co (co =每年的季节数)。则FXx(x) = Pt(0) + [1 - /3r((J)]FVTiVT>0(a)为z季节的累积分布函数,其中FXx{x) - PAX
2 .水流随机模拟
如果能建立连续时间内水流的随机模型,那么原则上就能得到日、月、年水流的性质和模型。有人根据物理原理,尝试建立连续时间流-流过程的模型然而,可以从这种连续时间模型推导出的聚合流模型在数学上变得很麻烦,而且对业务水文学的适用性有限理解模型和参数的升级规则一直是一个具有挑战性的研究课题。一般来说,大多数可用于连续时间和短时间尺度(如小时)水流模拟的模型都是基于物理或概念原理将降水转化为径流。因此,降水输入和流域水文循环的其他相关过程的随机特征被转化为随机的水流输出。这类模型的例子有SHETRAN26和PRMS.59, SHETRAN26模拟“连续”流沿着河流而PRMS是一个半分布式的概念模型,它模拟每小时和每天的流量。然而,在本节中,我们主要讨论随机水流模型,这些模型可以明确地从流域底层水文过程的物理或概念关系中推导出来,也可以直接从水流数据中推导出来。
连续时间到每小时和每天的流量模拟
要在连续时间尺度上模拟水流,就需要制定一种能够在大动态范围内再现水流波动的模型结构。如前所述,随机方法在连续时间和短时间尺度的水流建模中的应用受到了限制,因为在这些时间尺度上,降水-水流过程具有复杂的非线性关系。早期对每小时和每天的流量进行建模的尝试是基于标准化和转换后的自回归(AR)模型。然而,基本上基于过程持续性的随机模型并不能正确地解释每小时和每日流量曲线的上升边和衰退特征。此外,还提出了用于日常流动模拟的脉冲噪声或马尔可夫过程和传递函数模型,在再现上升翼和衰退方面取得了有限的成功
尽管如此,通过使用概念随机模型已经完成了一些有趣的工作,并取得了一些成功。例如,Kelman52应用了分水岭的概念表示,考虑到直接径流和地表和地下水储存的影响。直接径流采用PAR(l)模型,带有产生间歇性的指标函数,其他成分采用线性水库建模。Kelman的模型为田纳西州鲍威尔河的日流量产生了合理的结果。同样遵循Salas和obbeysekera96和Claps等人提出的方法,16 Murrone等人68提出了一个短时间径流的概念-随机模型。一个三级概念径流成分和一个随机地表径流模型流域的日响应。基流由三个线性储层模拟,分别代表具有年响应的深层含水层、具有年更新的含水层和地下径流.地表径流被认为是一个不相关的点过程。上述方案将降雨模拟为独立泊松过程,得到了一个多镜头噪声流-流过程。该模型能有效地再现水流变化。此外,通过将Kelman的概念方法与产品模型(94)和gamma AR模型(28)结合起来,并使用描述水流开始和水流衰退的指数衰减的三态马尔可夫链(1),对间歇性的每日水流过程进行了建模
每周,每月和季节性流量
单点周期模型。经季节标准化后,平稳随机模型可用于周流量、月流量和季节流量的建模。当季节与季节之间的相关性在全年中没有变化时,这种方法可能是有用的。一般来说,具有周期相关结构的模型,如周期自回归(PAR)和周期自回归与移动平均(PARMA)更适用。一个例子是PARMA(1,1) model97
yv,r =Hx +«HrOv。t-l +£v,r ~ 01,t£v,t- 10)
其中¿uT,(±>]z, T和a As:)是模型参数。当O为0时,模型(1)变成PARMA(1,0)或PAR(l)模型。低阶PARMA模型如PARMA(1,0)和PARMA(1,1)已广泛用于模拟月流量和周流量
PARMA模型可以从物理/概念原理中推导出来。考虑到流域中一年四季变化的所有水文过程和参数,季节性水流已被证明属于PARMA模型的范畴另外,还提出了一种具有周期独立残差的常参数模型季节性水流随机模型的理想特性之一是保存季节和年度统计数据。然而,简单的PAR(l)或PAR(2)模型很难实现这种统计数据的双重保存。因此,在20世纪70年代,水文学家转向了所谓的分解模型(参见第3节)。这种简单的PAR模型再现季节和年度统计数据的主要缺点是缺乏足够的相关结构。PARMA模型具有比PAR模型更灵活的相关结构,提供了保留季节和年度统计数据的可能性。一些水文学家认为帕尔马模型的参数太多了。然而,人们不能指望像PAR(1)这样的模型做得比它所能做的更多,即仅仅再现滞后-1个月之间的相关性,而不能再现较长时间滞后的相关性和更高阶聚合统计数据。再现季节和年度统计数据的另一种方法是乘法模型族。
Box和Jenkins5首先提出了乘法模型。这些模型具有将变量yV T与yvz_i和yv_l联系起来的特点。McKerchar和Delleur66采用对原始序列对数进行差分后的乘法模型来模拟和预测月流量序列。因为这样的乘法模型没有考虑到周期性的相关性,差分被用来试图减少或消除这种周期性。然而,他们无法重现协方差结构中的季节性,也无法建立考虑季节性的预测置信限。这个问题的出现是因为所提到的乘法模型不包括周期参数。可以克服上述限制的(具有周期参数的)模型是乘法帕尔玛模型例如,乘法PARMA(1,1) x(1.1) "模型被写成
zv。T = ^l ^v-l。T + 4>\,xZv,z-\ - + fiv。T ^
~®1,t£V-1, t ~~ $1, t£V,t -1 +®1,t ^1, t£V-1, t -1
其中,zV T - yVtX -¿uT和Oj T, @1t,
上述PARMA模型和乘法PARMA模型在模拟水文时间序列时的局限性是要求将底层序列转化为正态序列。另一种不具备这一要求的方法是PGAR(l)模型,用于对具有周期性相关结构和周期性伽马边际分布的季节流进行建模考虑y是一个具有三参数gamma边缘分布的周期相关变量,其位置Az、尺度aT和形状[iT参数随t变化,且t = 1 <»(t =季节数)。那么,新变量zv T = yV T - A是一个双参数gamma,可以用zv T = ^>TzV T_1 +(zv T_1) Twv r表示,其中(j), =周期自回归系数,ôz =周期自回归指数,wv T =噪声过程。该模型具有与PAR(l)过程等效的周期相关结构。它已被应用于美国几条河流的周流量序列。27所获得的结果表明,在再现通常用于流量模拟的基本统计数据方面,这种PGAR模型优于常规的基于模型(如对数变换后的PAR模型)。此外,还提出了一种非参数的水流模拟方法,这种方法能够精确地再现历史分布
PARMA和PGAR模型对于短时流的流动建模不太有用。在这些流中,流动是间歇性的,这是上述模型所不能表示的特征。相反,周期乘积模型更真实,其中Bv T是一个周期相关伯努利方程
(l,0)过程,zv T可以是一个具有给定边际分布的未校正或相关周期过程,B和z相互未校正。在文献14'94中已经报道了这些模型在模拟一些短暂流的间歇性月流量时的性质和应用
多点周期模型。在模拟多个地点的季节性水流时,通常使用多元PAR和PARMA模型。6'42'92,97例如,多元PARMA(1,1)模型为
其中Zv T = Yv z - |x;|x是一个列参数向量,包含元素yUt'\…, fi"'■S>T和0T为n × n个周期参数矩阵,噪声项ev T为正态分布的列向量,£(ev I) = 0,£(ev Te^T) = rT,对于k 0, E(£v x_k) - 0, n =站点数。此外,还假设ev T未被Zv t_1修正。该模型的参数估计可以用矩量法进行,但求解并不简单。删除(3)中的移动平均项,即所有t的0t = 0,产生一个更简单的多元PARMA(1,0)或PAR(l)模型。这种较简单的模型已广泛用于生成季节性水文过程。为了便于参数估计,可以对上述模型进行进一步简化。假设Eq.(3)中的
一年一度的河流
自回归(AR)、自回归及移动平均(ARMA)模型已成为单站和多站年流量模拟中最常用的模型。其中,低阶模型已广泛应用于生成年流量序列。29,42,61,62,72,92
单点静止模型。AR(1)模型定义为y, = n + 4>(y,-\ - n) + '<■,■其自相关函数pk = (f>pk, = 4>k随着时滞k的增加呈指数衰减。该模型一直是短记忆模型的原型,因为pk相对较快地趋于零,因此在E(R**) ~ nh中h - *■\相当快(R* " * =重新缩放的累积偏离样本均值的范围)。比AR(1)更通用的模型是由6,42,97给出的ARMA(1,1)
Y, = j" +(±b0 (yt-1 - j") + - (4)
它的自相关函数pk = (l - - 0)(l - 200 + d2)'1^'1比AR(1)模型更灵活,因为它依赖于两个参数(j)和9。的ARMA过程可以代表长记忆依赖,72'9'是许多河流的重要属性。AR和ARMA模型假设底层序列是正态分布的,这一假设并不总是适用于年流量序列。虽然可以通过将倾斜级数转换为近似正态级数来规避这一假设,但不需要转换的直接方法是可行的替代方案。伽马自回归(GAR)过程y, = - (j)) + <$>yt_\ + t],提供了这样一种替代方法,其中y,是伽马分布参数X, a和ft(分别是位置,尺度和形状参数),(j) =自回归系数,t], =噪声项。GAR(l)模型与AR(1)模型具有相同的自相关函数。GAR模型模拟年流量序列的估计程序和应用可在文献中找到
AR、ARMA和GAR模型可用于模拟多年生河流中的水流过程,但不适用于一些短暂河流中的水流流动等间歇性过程。间歇过程可以建模为y, = B,z,其中yt =非负间歇变量,Bt =相关(1,0)伯努利过程,z, =正值连续自相关变量,例如AR(1)过程,假设Bt和z相互不相关。因此,得到的产品过程yt是间歇的和自回归的。这些模式已被应用于短时降雨和间歇流过程的模拟。7’13’94最后,其他类型的模型,如分数高斯噪声。提出了64折线、6移位线、93和FARMA42来表示年流量时间序列的某些特殊性质。例如,移动水平模式具有模拟具有突然变化的时间序列的能力,这是在许多水文气候过程中观察到的一种特性。
多点静止模型。多个时间序列的建模是水文学研究中广泛需要的。考虑列向量Yt,元素y\V],…, vj"',其中n =考虑的序列数(变量数)。多元AR(1)模型定义为65
其中Zt = Yt - (x, |x是一个均值的列向量¿u(1),…, e,是正则噪声的列向量'<{1',…,,每个都是零均值,使得E(eteJ) - F和E(E,eJ_ k) - 0对于k 0, $和F是n × n个参数矩阵。另外,假设et与2t_x不相关。模型(5)是多序列短时记忆模型的原型,在水文作业中得到了广泛应用。29'42'62'92同样,多元ARMA(1,1)模型可以写成式(3),除了参数$和&不依赖于时间。
除低阶多元AR模型外,使用全多元ARMA模型往往会导致复杂的参数估计。73’92因此,提出了模型简化。例如,同期的ARMA (CARMA)
<1>和0为对角矩阵时的模型结果。Salas et al.,92 Stedinger et al.,106和Hipel and McLeod42提出的这个概念可以推广到一般情况。同时关系意味着只有y的并发值的相关性被认为是重要的。此外,参数矩阵的对角化允许“模型解耦”为组件单变量模型,这样模型参数就不必联合估计,并且可以采用单变量建模程序。因此,在每个r},'\ / = 1未校正,但同时与方差-协方差矩阵t相关的每个点拟合单变量ARMA(p, q)模型。因此,可以使用单变量估计程序估计每个模型中的参数's和0's, e可以用e, = Bq建模,其中£与e (| = / and) = 0对于k ^ 0是正常的。注意,不必为每个站点考虑相同的单变量ARMA(/;, q)模型。
3 .时空分解模型
分解模型,即时间和/或空间上的降尺度模型,一直是随机水文学的重要组成部分,这不仅是因为我们对理解和描述水文过程的空间和时间变异性特征的科学兴趣,而且是因为实际工程应用。例如,许多水文设计和操作问题需要每小时的降水数据。由于每小时降水数据不像每日数据那样普遍可用,一个典型的问题是将每日数据缩小或分解为每小时数据。同样,为了简化包含大量降水和径流站的大型系统的分析和建模,需要采用时间和空间分解程序。本节简要回顾了降水和径流时空分解的一些经验和数学模型和程序。
降水分解
通常情况下,在一个给定的时间间隔内定义的站点降水数据被分解为更小时间间隔的降水是经验完成的例如,通过使用表格或图表,可以将24小时(每日)降水分解为6小时降水。更完整的解体方案已经发展出来。Hershenhorn和Woolhiser41考虑了日降雨量和一个模型,以获得风暴数量、数量、持续时间和每个风暴到达时间的日内量级。他们表明模拟的降雨序列与观测值比较好。上述模型虽然具有创新性,但并不令人满意,即模型比较复杂,需要对原始数据进行多次转换才能得到合理的结果。另一个缺点是在考虑的间隔数量上缺乏灵活性。
Cadavid等人开发了另一种正式的短期降雨分解方案。11分解模型假设PWN和NSWN
(请参阅第1节)作为潜在的降雨产生机制。PWN模型的分解算法的制定基于时间间隔内总降水量Y条件下的到达次数N的分布,给定N和Y的白噪声项的分布,以及N条件下的到达次数的分布,算法在使用模拟PWN样本时表现良好。基于NSWN模型的分解方案更为复杂。它在模拟和记录的样品上表现良好,只要所使用的模型参数与在分解尺度上控制过程的参数相似。主要缺点是不同聚集级别的参数估计不兼容,如第1节所指出的。最近,人们提出了一种基于人工神经网络的降雨分解方法
Epstein和Ramirez24根据所给出的Valencia和Schaake111的分解模型,建立了一个多尺度线性回归统计气候反演方案raybet雷竞技最新雷竞技csgo
其中,Y为降尺度水文气候值(如降水)矩阵,X为升尺度水文气候值矩阵,a和B为参数矩阵,s为独立标准正偏差矩阵。上式中的所有项都是时间的函数,降尺度模型通过大尺度场x的时间演化以时间为条件,基于矩的方法进行参数估计,可以在所有聚集层上保留一阶和二阶矩。
分流数据的分解
低阶PAR模型在模拟季节流时再现年流量统计数据的缺点导致了分解模型的发展,如Valencia-Schaake模型(6)。在该模型中,季节流的建模和模拟分两个或两个以上步骤完成。首先对年度流量进行建模,以便再现所需的年度统计数据[例如,基于ARMA(1,1)模型];然后生成合成的年流量,再通过式(6)分解为季节流量。虽然保留了季节流量数据的方差-协方差特性,并且生成的季节流量加起来等于年流量,但模型(6)没有保留每年第一个季节和任何之前季节的协方差。为了克服这一缺点,式(6)被修改为i = AX + Be + CZ,其中C是一个额外的参数矩阵,Z是每个站点前一年(通常只是前一年的最后一个季节)的季节值向量有人提出了进一步的改进和修正,假设一个年度模型重现S%x和Sxz,以及一个不依赖于年度模型结构但重现Syy、SYX和Sxx.'05的方案
上述的分解模型有太多的参数,特别是当站点数量大而可用的历史样本量小时,这个问题可能是显著的。Lane56将上述分解模型中的一些参数设置为零,以便
Yz =ATX + B,e + CtFt_!t = 1,……(u (7)
是一个参数较少的模型。在文献中可以找到参数估计和适当的调整,以便使每个地点的季节值与年值精确相加
如果分解是一步一步(阶段或级联)完成的,估计问题可以简化,这样所涉及的矩阵的大小,从而减少参数的数量例如,每年的流量可以在一个步骤中直接分解为每月流量(这是通常的方法),或者可以在两个或多个步骤中分解为季度流量,例如,在第一步中分解为季度流量;然后,在第二步中,每个季度的流量进一步分解为每月的流量。然而,即使采用后一种方法,当季节数量和站点数量很大时,也会产生相当大的矩阵规模。Santos和Salas98提出了一种分步分解方案,每一步分解总是分成两个部分或两个季节。该方案导致单站点分解的最大参数矩阵大小为2 x 2,多站点分解的最大参数矩阵大小为2n x 2n。还提出了重现季节性统计数据的分解模型,以及假设季节性和年度流量为对数正态的季节性流量和年度流量的季节性流量与年度流量的协方差。此外,还提出了基于非参数度量方法的时间分解方法。
尽管分解是随机水文学的一个重大发展和实用工具,但为什么某些周期模型不能再现年度统计数据的问题仍然存在。因此,在20世纪70年代和80年代初,人们提出并发展了更复杂的模型,如PARMA模型。obbeysekera和Salas70以及Bartolini和salas已经探索了它们在季节之外再现统计特性的能力
4种时空聚集模型
与分解一样,聚合(升级)建模方法在两个或两个以上的聚合或时间尺度上处理流过程。然而,这两个概念是完全不同的。在分解过程中,建模和生成过程是向后的,即先建模并生成年流量,然后在连续的分解步骤中获得月、周、日流量。而在时间聚合中,则是正向的,即先对日流量建模生成,然后依次对周、月、年流量建模生成。聚合方法的基本前提是连续时间尺度上的随机特征决定了任意级别的聚合或时间尺度上的随机特征。文献中已探讨了不同时间尺度上统计数据之间的关系
112假设月流量遵循PAR(l)或PARMA(1,1)过程,则得到的年流量模型为平稳ARMA(1,1)。上述概念和结果揭示了不同时间尺度的水流模型(及其参数)之间的结构联系和兼容性。非洲考利科洛的尼日尔河的水流数据被用来说明一些聚集概念,特别是在用PAR(l)和PARMA(1,1)模型对季节流量进行建模时,与重现年度相关结构有关结果表明,在比较由季节流量模型推导出的ARMA(1,1)年流量模型的参数和相关图时,用PARMA(1,1)模型得到的结果明显优于用PAR(l)模型得到的结果。此外,得到的结果取决于一年中考虑的季节数量(例如,月,季度),并且随着一年中季节数量的减少,得到了更好的结果。
Bartolini和Salas3扩展了聚合的概念,不仅包括从季节到一年的聚合,还包括从周到月、从月到季节、从季节到年的聚合。例如,一个PARMA(2,1)月流量的聚合可以得到一个PARMA(2,2)双月流量;反过来,这种PARMA(2,2)双月流量的聚合也给出了季度流量的PARMA(2,2)。此外,如果将这些季度流量汇总为年度流量,则该模型为平稳ARMA(2,2)。将部分聚集概念应用于尼日尔河的季节和年流量,结果表明,PARMA(2,1)和PARMA(2,2)模型在再现年流量的方差-协方差特性方面优于其他模型。聚合概念在不同时间尺度上对尼日尔河的季节性和年度流量建模的应用表明,如果想重现季节性和年度一级和二级统计数据,就需要使用PARMA模型进行流量建模和模拟。传统的模型,如PAR(l),在模拟诸如尼日尔这样的流动时是完全不足的。通常模拟季节和年流量的方法是针对不同的时间尺度使用不同的模型,忽略了不同时间尺度模型之间的兼容性。本节中讨论的聚合概念和结果指出,必须避免采用这种传统的方法和模型进行水流模拟。
类似于时间聚合的推理适用于流过程的空间聚合。例如,可以假设一个流网络由许多一阶、二阶和三阶流组成。首先考虑在两个一阶流的交界处建模。自然地,在结的直接下游站点的模型必须从两个上游站点定义的二元模型推导出来,每个支流一个。反过来,当二阶流与另一个流连接时的流的模型,也就是说,二阶流必须定义从结处直接下游的流的模型,等等,因为流在流网络中传播。因此,水流模型必须在时间和空间尺度上兼容。
5 .扩展问题和缩减问题
了解、描述和建模局部、区域和全球气候及其与水文、生物物理和生物地球化学过程的非线性相互作用是目前地球科学中最具挑战性的问题之一。raybet雷竞技最新这不仅是治理过程和边界条件的高度空间和时间可变性,而且这种可变性发生的尺度范围很广。分布式水文模型需要高分辨率的输入数据。在所有水文变量中,降水在陆地表面-大气界面的水和能量收支中起着至关重要的作用,降水在水文和大气模型中的准确表示至关重要。降水是大气和陆地表面过程相互交织的结果。它在时间尺度上有极大的变化,从秒到年,从不到米到数百公里的空间尺度上。水文行为对降雨时空变异性的敏感性是降水与控制降雨转化为土壤水和径流的地表特征之间非线性相互作用的结果。降水建模需要对统计学的理解空间结构时间降水和对时空尺度范围内支配降水演变的物理过程的理解。由于尺度差异,耦合全球(或区域)大气模式和水文模式需要降雨降尺度。一般来说,降尺度方案可以分为两大类,动态降尺度方案和统计降尺度方案。
在动态方案中,区域和地方尺度上的气候和土raybet雷竞技最新地利用变化情景是使用区域和地方大气模式开发的,例如科罗拉多州立大学的区域大气模式系统(RAMS)。这些模式是由观测和全球大气模式输出的边界条件驱动的。通过这种方式,大气模型充当了一个基于物理的动态插值器(即基于物理的降尺度)。RAMS已与陆地表面方案(LEAF-2)、水文模型(TOPMODEL)和区域生态系统模型(CENTURY)耦合。因此,动态方案明确地编码了多个非线性和复杂的局部和区域相互作用和反馈。然而,试图使用基于物理的模型在不断减小的尺度上解析过程,会迅速导致计算效率低下,并受到对小尺度物理过程行为理解不足的限制。其他大气模式,如NCAR模式33和宾夕法尼亚州立大学/NCAR中尺度模式版本5,19已用于动态降尺度。
在统计降尺度中,获得了气候变率,特别是降水的亚网格时空尺度细节,从而保留了水文气候场时空变率的统计特征作为尺度函数。统计技术通常基于线性或非线性回归,非线性动力学,人工神经网络,马尔可夫过程,乘法随机级联模型等方法。回归方法的局限性之一是,只有在确定大尺度参数与区域和局部气候之间存在很强的关系时才适用(通常情况下并非如此),而且它们仅在观测的空间和时间范围内有效。raybet雷竞技最新虽然统计降尺度在计算上是有效的,但它不能明确地包括上述亚网格尺度的物理反馈,并且很难将大气过程与区域生态和水文过程耦合起来。另一方面,基于乘性随机级联模型的统计降尺度方法可以以相对较少的计算量再现降水场在空间和时间上的尺度特征(即尺度不变性)、聚类和间歇性特征。
迄今为止,文献中提出的降尺度方法大多只处理降水场的空间变异性,而对降水场的时间演化的描述通常与空间降尺度无关。唯一考虑到的时间相关结构是由大气模式在更大的空间尺度上产生降水场的动力学所导致的,或者是在观测的时间演化中编码的。因此,总的来说,这些方案并没有完全正确地解释亚格尺度降水场的时间相关结构(即持久性)。
动力降尺度
动态降尺度可以考虑四种基本类型的模式:一种类型强烈依赖于大尺度数值天气预报横向边界条件、底部边界条件和初始条件。第二种类型忘记了初始条件,但依赖于观察到的横向和底部边界条件。第三种类型是运行大尺度模型时,只强制使用表面边界条件,输出用于降尺度区域模型.第四种类型是使用真正的全球气候模式(包括海洋、大气、大陆海冰、景观过程等raybet雷竞技最新)为区域模式提供横向边界条件。这是政府间气候变化专门委员会(IPCC)的降尺度方法,但IPCC的方法只包括有raybet雷竞技最新限的一组地球系统强迫(例如,二氧化碳的辐射效应,太阳日晒)。用例子总结(IC =初始条件;LBC =横向边界条件,BBC =底部边界条件;类型1 ETA4使用观测到的IC、LBC和BBC;2型PIRCS34”35使用观察到的LBC和BBC;与观测到的SSTS102结合的CCM3强制的3型ClimRAMS使用观测到的BBC;第4类地球系统全球模型使用区域模型缩小规模当我们从类型1移动到类型4时,对解决方案的观测约束变得越来越少。 Thus预测能力会从1型减少到4型。
对于当前的模型,如大气-海洋模型全球环流模式(aogcm),无论是aogcm还是区域模式(4型模式)都不包括所有显著的人类对气候系统的影响。raybet雷竞技最新土地利用变化的综合效应、对大气的生物地球化学效应(例如由于二氧化碳的增加)以及污染气溶胶的微物理效应尚未包括在这些模式中。因此,现有的模型运行只能被解释为敏感性实验,而不是预测、预测,甚至场景
此外,在动态降尺度方面,按照目前的应用,即使包括所有重要的大尺度(GCM尺度)人为干扰,也没有从区域模型中反馈到AOGCM。AOGCM的空间分辨率也不足以正确定义区域模型的横向边界条件。Anthes和Warner2表明,横向边界条件是区域大气模式的主要强迫因素,与区域大气模式的传播特征有关极地西风带.在数值天气预报(类型1和2模式)中,用于初始化模式的分析中使用的观测数据即使退化为全球模式的较粗模式分辨率,也保留了现实主义成分。当使用区域数值天气预报模式的横向边界条件时,这种现实主义会持续一个星期左右。对于aogcm来说,情况并非如此,因为它不存在影响预测的数据。一个区域模型不能重新插入模型技能,当它如此依赖于横向边界条件时,无论该区域模型有多好。
统计降尺度
RAMS等中尺度大气模式的输出或来自NEXRAD(下一代雷达)网络的观测数据的网格尺寸通常比与分布式水文模式相关的网格尺寸(例如,在10°m量级)更大[例如,0(103至104)m]。地表系统响应来自大气的激励,例如降水,并通过évapotranspiration和潜热通量将水分反馈到大气中。在包括< 0(104)m在内的大尺度范围内,激励和响应在空间上是异质的,这种亚网格的空间变异性对高尺度和低尺度地表通量的大小和分布有显著影响,它们之间的相互作用是非线性的。解释这种时空异质性对于水文建模和描述陆地表面-大气相互作用很重要。此外,统计降尺度除了要求aogcm是对未来的准确预测外,还要求用于降尺度的统计方程在区域大气和地表条件变化下保持不变。没有办法检验这个假设。事实上,它不太可能成立,因为区域气候对更大尺度的气候条件不是被动的,而是随着时间的推移而变化,并反馈到更大尺度raybet雷竞技最新。关于这一担忧的更多细节已被报道。
回归计划。大尺度和局地尺度气候场之间的关系可以通过基于回归的方案建立。最直接的降尺度方法是直接插值。该方法适用于海平面压力、温度等平稳变化的场,但不适用于降水等非平稳间歇场。回归方案的一些例子是(1)一种方法(基于主成分分析、典型相关和回归分析)称为气候预测
-
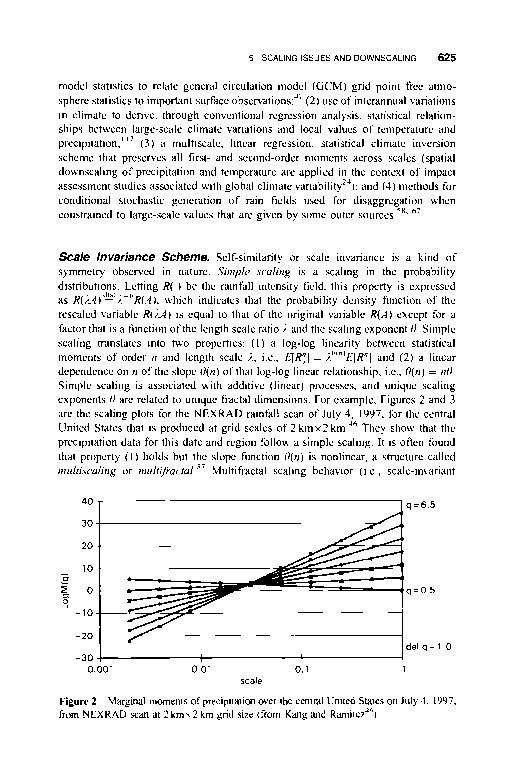
- 图3 1997年7月4日,2 km × 2 km网格尺寸下美国中部降水的NEXRAD扫描的边际矩斜率对数-对数标度函数(来自Kang和Ramirez46)。
在空间上发现了标度指数的行为雨量分布
37岁,75109
以及降雨的时间分布。此外,降水的尺度不变性和间断性都可以用来建立精简的降雨随机模型
已使用乘法随机级联来生成分形场,模拟观测到的降雨的缩放指数的频谱。级联发生器根据其产生的标度谱进行选择。值得注意的是,提出了通用多重分形、109 the /j-modcllX或log-Poisson模型101。为了说明,我们将在下面讨论随机级联模型
离散的随机级联将质量分布在^维立方体的连续规则细分上。这个过程的示意图如图4所示。初始立方体长度标为L0,每层被细分为b等份,其中b > 2d为分支数。细分n层后的第z个子立方体记为A'n(第n层有i = i ' b"个子立方体),子立方体A'n的长度标度记为Lm,无量纲空间标度定义为Xn = LJL0 = b~nld。质量在立方体上不同层次的分布如下所示。首先,初始立方体(级别n = 0)被分配非随机密度R0,即初始质量RqLq。子立方A\, i ~…, b在第一个细分后(在级别n = 1)被赋予密度R(j Wx(;),即质量R0L!\Wx(i),其中W是独立和同分布(iid)随机变量-级联发生器。这个乘法过程持续到级联的所有n层,因此子立方体A n的质量为
Hn {K) = R0LdnY \ Wj{我)。
其中E[W] = 1;因此,质量在随机级联的所有水平上是平均守恒的。
5缩放问题和OOWNSCALING 627分支数-*!参数:p.y.o
第三级联

第三级联
Ria-S ^ W。WjWj
(a)离散随机级联模型
图4二维离散随机级联模型示意图:(a)离散随机级联模型(来自Kang和Ramirez46)。
Dimb9^4 paiamAfr fr m降水和STflEAMFLOW过程的随机模拟。
-

- 第三级联(o-3)

(b) reratanmiftnc hjaarciBcaJ randtm cascade modd
图4二维离散随机级联模型示意图:(b)非参数随机级联模型(来自Kang和Ramirez4*)。
得到级联极限质量为n - >oc。它被认为是简并的如果总质量为零,概率为1。非简并性依赖于W的分布,它要求满足条件E[W] - 1。子立方体/(^(Aj,)中的极限质量满足递归关系:¿^(Aj,) = fin(a 'n)Z^(i),对于i= 1 b"其中iid随机变量,分布为Zx = /j^(A0)/
/in(An) =¿uoo(A0)/7?0Z0 for all i, n. The cascade limit mass ¿/^(AJ,) is given by the product of a large-scale low-frequency component ¿u„(A'n), and a subgrid subgrid (i.e., subcube) scale high-frequency component Z^(z'). The latter term represents subgrid-scale variability at each level of cascade development.
随机级联表现出矩尺度行为,由此可以估计级联发生器W的性质。样本空间矩定义为Mn(q) = XlLi tioo(A'n),其中q =矩阶(对于q - 0,只有非零极限质量包含在和中)。对于较大的n,样本矩应该收敛于集合矩,但由于它们在n -►oo时发散到无穷大或收敛到零,因此考虑矩随尺度的收敛/发散率。在随机级联中,集成矩显示为Xn尺度的log-log线性函数。这种比例关系的斜率称为Mandelbrot-Kahane Peyriere (MKP)函数:/j,(q) = \ - q + log/;E \ Wq]。MKP函数包含了关于级联发生器W分布的重要信息,从而表征了降雨的尺度特性。类似地,样本矩比例关系的斜率可以定义为z(q) = lim, _^n[log Mn(q)/ - log kn]。对于较大的n(如xn0)和特定的q范围,样本矩和集成矩的矩标度关系的斜率收敛,即r(q) = dyh(q)。在数据分析中,利用样本矩的尺度估计z(q)函数和级联发生器的分布,从而推断级联模型的参数。
对于间歇性的时空降雨数据,P(W = 0)最好为正。为此,级联发生器W的间歇模型被写成W = BY,其中B是所谓的/i模型的间歇发生器,Y是严格的正随机变量。/ ?模型根据以下概率将域分为多雨和非多雨部分:P(B = 0) = 1 - B -1 "和P(B = b1 ") =其中(i是一个参数,E[B] = 1。ji模型不考虑极限质量¿u”(A’”)的大尺度分量的正部分的可变性(在每一层n,它假设非随机值R0LndbP”)。积极的可变性
继续阅读:降水和水流过程的随机预报
这篇文章有用吗?
读者的问题
-
奥马尔一年前
- 回复